Pythonで正規分布乱数を生成してヒストグラムと基本統計量をチェック

　ExcelVBAで正規分布乱数を生成してヒストグラムと基本統計量をチェックの内容をPythonで実施してみました。Pythonはライブラリーに便利な機能が多いので、かなり楽でグラフ化も簡単です。この領域は、ExcelVBAよりもPythonの利用が効率的といった印象です。

プログラムの作成

　プログラムでは以下の計算を実施しています。

1. 正規乱数の発生と、生成された乱数のパラメータ推定
2. 入力パラメータによる正規確率密度関数の算定
3. パラメータの推定値を用いた正規確率密度関数を算定

正規分布の乱数生成

　Numpyのrandom.normal関数を用いました。ここでは、Numpyをnpと定義しているので、次のコマンドになります。

np.random.normal(平均，標準偏差，個数)

平均値、標準偏差の推定

　NumPyのmean、std関数を用いました。

平均値：np.mean(配列)　　標準偏差：std(配列)　

正規密度関数の設定

　ｘ軸の値を等差数列で作成し、y軸の値をxの値に対応する正規分布の確率密度関数値としています。

等差数列：np.arange(初期値，最終値，等差値)

　正規分布の確率密度関数は、SciPyのstatsサブパッケージを用いています。

正規分布の確率密度関数：norm.pdf(変数，平均値，標準偏差)

ヒストグラムの図化

ax.hist(変数, label=’凡例名‘,alpha=透過率,density=True,range=(レンジの始まり,終わり),bins=分割数)

• ax：このプログラム中で図figureの１つのプロットの名として定義
• densityはTrueの場合に正規化した値となる。

凡例の図化：plt.legend()

プロットのタイトル

ax.set_title()

出力結果とグラフ

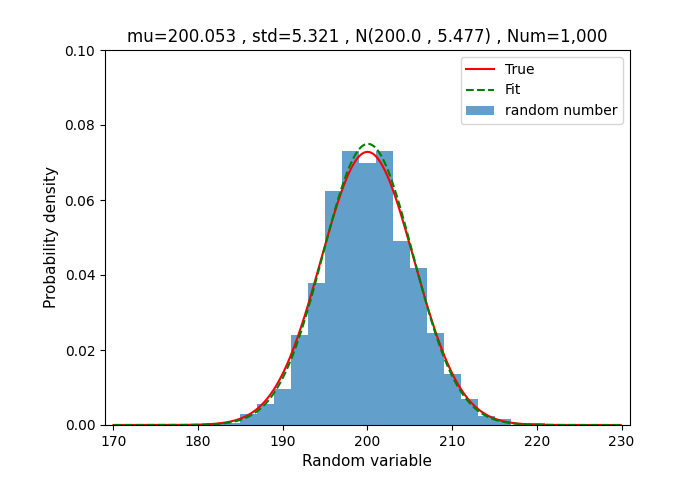
　左下のグラフは乱数1,000個発生させた場合のヒストグラムと正解の正規確率密度関数（凡例：True）、乱数から推定した正規確率密度関数（凡例：Fit）を重ねた図です。1,000個ではまだ十分な近似とはいきません。

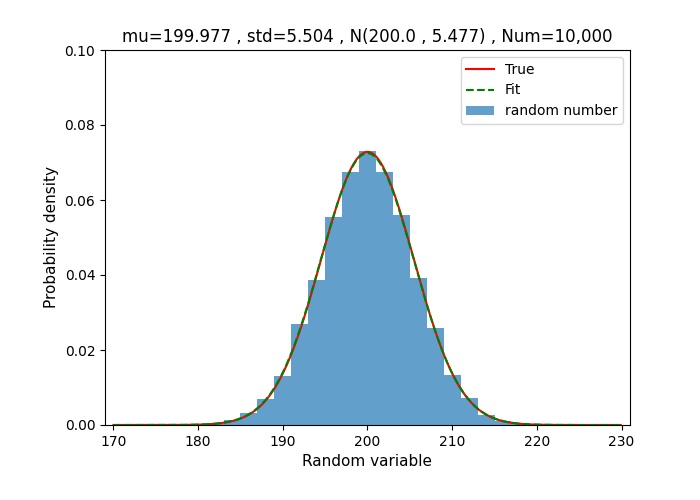
　右下のグラフは乱数10,000個発生させたもので、正解と乱数から推定した正規確率密度関数がほぼ一致しています。

　これらグラフはPythonのライブラリを利用して描いたものですが、ExcelVBAのような煩わしさがなく、正確に図化されています。

まとめ

　今回は、ExcelVBAで正規分布乱数を生成してヒストグラムと基本統計量をチェックの内容をPythonで実施してみましたが、ライブラリの機能の豊富さから、Pythonが勝る結果となりました。モンテカルロシミュレーションについても、比較してみたいと思います。