Excel2013VBAで微小振幅波の波長の計算を行います。
まず、繰り返し収束計算の定式化です。
微小振幅波の波長
微小振幅波の波長は、次式で与えられる。
$$L=\frac{gT^2}{2π}tanh\frac{2πh}{L}\tag{1}$$
ここに、\(L\):微小振幅波の波長(m)
\(T\):波の周期(s)
\(g\):重力加速度(9.80m/s2)
\(h\):水深(m)
\(π\):円周率
水深が波長の1/2より深いときは、
$$tanh\frac{2πh}{L}≃1$$
の近似が成り立つので式(1)は、
$$L_0=\frac{g}{2π}T^2\tag{2}$$
ここに、\(L_0\)は深海波の波長である。
一方、水深が波長の1/20より浅いときは、
$$tanh\frac{2πh}{L}≃\frac{2πh}{L}$$
の近似が成り立ち、式(1)は、
$$L=\sqrt{gh}・T\tag{3}$$
このような波は長波または浅海波と呼ばれる。
式(2)や式(3)が成立する条件での波長計算は簡単であるが、その間の条件の場合には、式(1)を繰り返し計算により解く必要がある。
波長式の変換
さて、右辺にある\(L\)の値を入れた際に計算される左辺の\(L\)との差がゼロとなるような収束計算を実施する。
式(1)が成り立つ波長を\(L_1\)として、式(2)を代入すると、
$$L_1=L_0・tanh\frac{2πh}{L_1}$$
両辺を\(2πh\)で割って、
$$\frac{L_1}{2πh}=\frac{L_0}{2πh} tanh\frac{2πh}{L_1}$$
ここで、
$$X_0=\frac{2πh}{L_0} , X_1=\frac{2πh}{L_1}\tag{4}$$
とおくと、
$$\frac{1}{X_1}=\frac{1}{X_0}tanh X_1$$
よって、
$$X_1=\frac{X_0}{tanh X_1}$$
両辺の差をとって、
$$f(X_1)=X_1-\frac{X_0}{tanh X_1}\tag{5}$$
と定義すれば、\(f(X_1)\)がゼロになるような\(X_1\)の値を求めればよい。
Newtonの逐次近似法の適用
さて、\(f(X)\)がゼロとなる\(X\)を求めるために、Newtonの逐次近似法を用いる。Newtonの逐次近似法は、\(X_1\)における勾配\(f'(X_1)\)を求めて、この勾配の直線を\(f(X_1)\)の点から引いてX軸と交わる点(\(f(X)=0\))のX座標を\(X_2\)とすると、
$$f’(X_1)=\frac{f(X_1)}{X_2- X_1}$$
$$∴X_2=X_1-\frac{f(X_1)}{f’(X_1)}\tag{6}$$
\(f'(X_1)\)は、式(5)を\(X_1\)に関して微分すると、
$$f'(X_1)=1+\frac{X_0}{sinh^2 X_1}\tag{7}$$
式(6)に式(5)と式(7)を代入すれば、
$$X_2=X_1-\frac{X_1-\frac{X_0}{tanh X_1}}{1+\frac{X_0}{sinh^2 X_1}}\tag{8}$$
よって、式(8)に\(X_1\)の値を入力して得られた\(X_2\)を\(X_1\)とおいて計算、これを繰り返し、次式で定義される誤差を0.001以下になるまで実施する。なお、\(X_1\)の初期値は\(X_0\)とする。
$$|1-\frac{X_1}{X_2}|≦0.001$$
求められた\(X_2\)を式(4)の関係から波長に変換すると求める解となる。
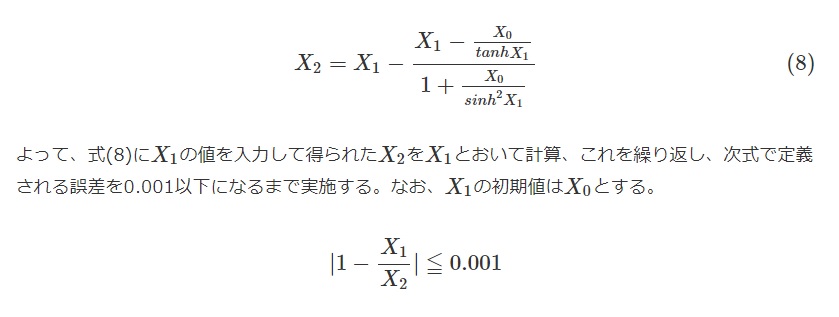

コメント