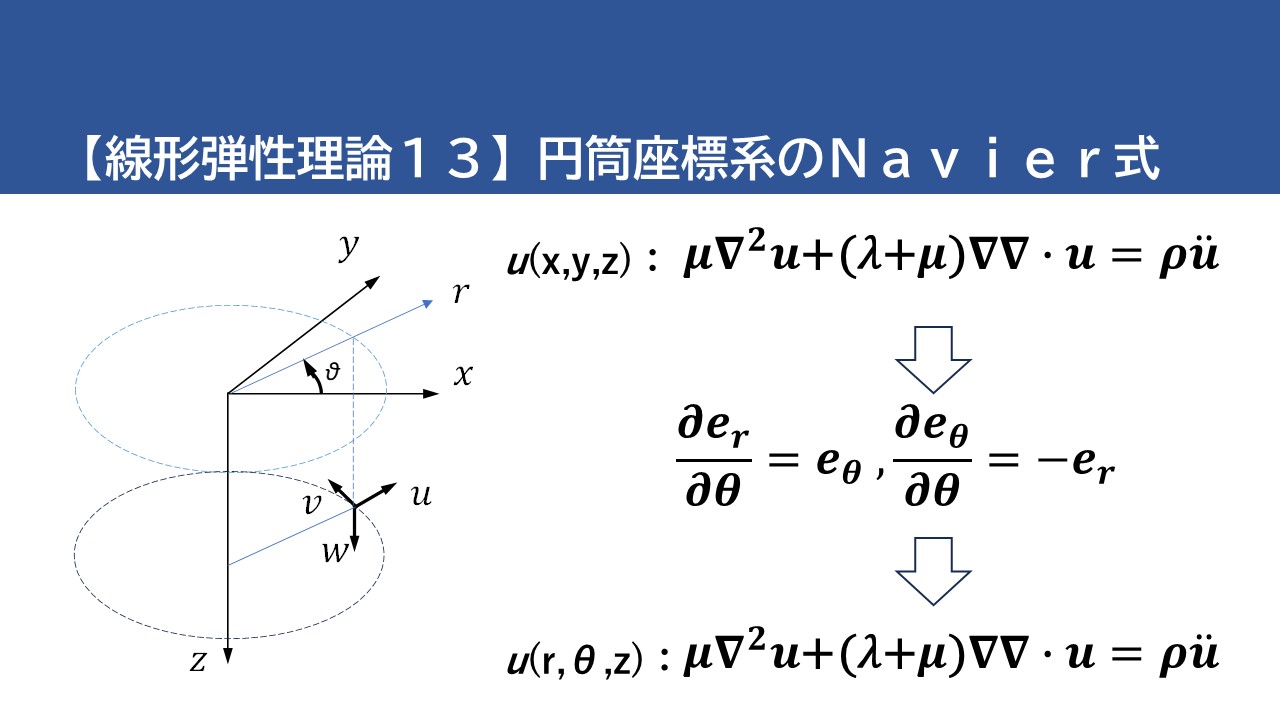
今回は前回までの座標変換を用いて円筒座標系のNavier式を導きます。変位ベクトルのアプラシアンの計算では、単位ベクトル \(e_r\) と \(e_θ\) の \(θ\) に関する偏微分によって単位ベクトルが変わることに注意する必要があります。ラプラシアンを単なる座標変換するだけでは、正しいNavier式を導くことはできません。確かに \(θ\) が \(Δθ\) だけ増分すると \(e_r\) は \(Δθ\) だけ回転した方向に変わりますし、\(e_θ\) の変化は \(-e_r\) 方向となります。
結局、直交座標系では各座標で同様な微分方程式の形となりますが、円筒座標系では \(r\) 方向と \(θ\) 方向の式に余分な偏微分を加える必要が出てきます。
直交座標系のNavier式
Navier式は式(85)、式(86)にて導いています(線形弾性理論9を参照)が、改めて表示すると次のようになります。
$$μu_{i,jj}+(λ+μ)u_{j,ji}=ρ\ddot{u}_i\tag{150}$$
$$μ\mathbf{∇}^2\mathbf{u}+(λ+μ)\mathbf{∇∇}・\mathbf{u}=ρ\ddot{\mathbf{u}}\tag{151}$$
直交座標系(\(x\) , \(y\) , \(z\))の変位を \(u_x\) , \(u_y\) , \(u_z\) 、単位ベクトルを \(i_x\) , \(i_y\) , \(i_z\) と置くとナブラ \(\mathbf{∇}\) は、
$$\mathbf{∇}=\frac{\partial }{\partial x}i_x+\frac{\partial }{\partial y}i_y+\frac{\partial }{\partial z}i_z\tag{152}$$
ラプラシアン \(\mathbf{∆}\) は、
$$\mathbf{∆}=\mathbf{∇}^2=\mathbf{∇・∇}=\frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial y^2}+\frac{\partial ^2}{\partial z^2}\tag{153}$$
となります。
変位ベクトルの発散(ダイバージェンス)は、
$$\mathbf{∇・u}=\frac{\partial u_x}{\partial x}+\frac{\partial u_y}{\partial y}+\frac{\partial u_z}{\partial z}\tag{154}$$
さらに、
$$\mathbf{∇∇・u}=\frac{\partial }{\partial x}\mathbf{∇・u}\enspace i_x+\frac{\partial }{\partial y}\mathbf{∇・u}\enspace i_y+\frac{\partial }{\partial z}\mathbf{∇・u}\enspace i_z\tag{155}$$
変位ベクトルのラプラシアンは、
$$\mathbf{∆}\mathbf{u}=\mathbf{∇}^2\mathbf{u}=\mathbf{∇・∇u}=\mathbf{∇}^2u_xi_x+\mathbf{∇}^2u_yi_y+\mathbf{∇}^2u_zi_z\tag{156}$$
したがって、\(x\)方向、\(y\)方向、\(z\)方向のNavier式は次のようになります。
$$μ\Bigl(\frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial y^2}+\frac{\partial ^2}{\partial z^2}\Bigr)u_x\qquad \qquad \qquad \qquad \qquad \qquad \qquad $$
$$+(λ+μ)\Bigl(\frac{\partial^2 u_x}{\partial x^2}+\frac{\partial^2 u_y}{\partial x\partial y}+\frac{\partial^2 u_z}{\partial x\partial z}\Bigr)=ρ\frac{\partial^2 u_x}{\partial t^2}\tag{157.a}$$
$$μ\Bigl(\frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial y^2}+\frac{\partial ^2}{\partial z^2}\Bigr)u_y\qquad \qquad \qquad \qquad \qquad \qquad \qquad $$
$$+(λ+μ)\Bigl(\frac{\partial^2 u_x}{\partial x\partial y}+\frac{\partial^2 u_y}{\partial y^2}+\frac{\partial^2 u_z}{\partial y\partial z}\Bigr)=ρ\frac{\partial^2 u_y}{\partial t^2}\tag{157.b}$$
$$μ\Bigl(\frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial y^2}+\frac{\partial ^2}{\partial z^2}\Bigr)u_y\qquad \qquad \qquad \qquad \qquad \qquad \qquad $$
$$+(λ+μ)\Bigl(\frac{\partial^2 u_z}{\partial x\partial z}+\frac{\partial^2 u_y}{\partial y\partial z}+\frac{\partial^2 u_z}{\partial z^2}\Bigr)=ρ\frac{\partial^2 u_z}{\partial t^2}\tag{157.c}$$
変位ベクトルのラプラシアン
円筒座標系(\(r\) , \(θ\) , \(z\))の変位を \(u_r\) , \(u_θ\) , \(u_z\) 、単位ベクトルを \(e_r\) , \(e_θ\) , \(e_z\) と置くとナブラ \(\mathbf{∇}\) は、式(125)(線形弾性理論11を参照)より、
$$\mathbf{∇}=\frac{\partial }{\partial r}e_r+\frac{\partial }{\partial θ}\frac{1}{r}e_θ+\frac{\partial }{\partial z}e_z\tag{158}$$
変位ベクトルの発散(ダイバージェンス)は式(129)(線形弾性理論11を参照)より、
$$\mathbf{∇・u}=\frac{1}{r}\Bigl(\frac{\partial }{\partial r}(ru_r)+\frac{\partial u_θ}{\partial θ}+\frac{\partial }{\partial z}(ru_z)\Bigr)$$
$$=\frac{u_r}{r}+\frac{\partial u_r}{\partial r}+\frac{1}{r}\frac{\partial u_θ}{\partial θ}+\frac{\partial u_z}{\partial z}\tag{159}$$
さらに、
$$\mathbf{∇∇・u}=\frac{\partial }{\partial r}\mathbf{∇・u}\enspace e_x+\frac{\partial }{\partial θ}\mathbf{∇・u}\frac{1}{r}\enspace e_θ+\frac{\partial }{\partial z}\mathbf{∇・u}\enspace e_z\tag{160}$$
つぎに、円筒座標系での変位ベクトルのラプラシアンでは、単位ベクトルの偏微分によって単位ベクトルの方向が変わることに注意が必要です。\(θ\) が微少変化する時の \(r\) 方向べクトルは \(θ\) 方向に、 \(θ\) 方向べクトルは \(-r\) 方向に変化することになります。これは円筒座標系で \(θ\) を \(Δθ\) 変化した場合の単位方向ベクトルの変化を図化して考えれば分ります。
つまり単位ベクトルの偏微分は、
$$\frac{\partial e_r}{\partial r}=0 , \frac{\partial e_r}{\partial θ}=e_θ , \frac{\partial e_r}{\partial z}=0$$
$$\frac{\partial e_θ}{\partial r}=0 , \frac{\partial e_θ}{\partial θ}=-e_r , \frac{\partial e_θ}{\partial z}=0$$
$$\frac{\partial e_z}{\partial r}=0 , \frac{\partial e_z}{\partial θ}=0 , \frac{\partial e_z}{\partial z}=0$$
変位ベクトルのラプラシアンは次式を実行することで得られます。
$$\mathbf{∇}^2\mathbf{u}=\mathbf{∇}(\mathbf{∇}・\mathbf{u})-\mathbf{∇}∧\mathbf{∇}∧\mathbf{u}\tag{161}$$
\(\mathbf{∇}∧\mathbf{u}\) は式(130)(線形弾性理論11を参照)から、
$$ \mathbf{∇}∧\mathbf{u}= \frac{1}{r}\begin{vmatrix} e_r&re_θ&e_z\\\frac{\partial }{\partial r}&\frac{\partial }{\partial θ}&\frac{\partial }{\partial z}\\ u_r & ru_θ & u_z\end{vmatrix}$$
$$=\frac{1}{r} e_r\begin{vmatrix} \frac{\partial }{\partial θ}&\frac{\partial }{\partial z}\\ ru_θ & u_z\end{vmatrix}-e_θ \begin{vmatrix} \frac{\partial }{\partial r}&\frac{\partial }{\partial z}\\ u_r & u_z\end{vmatrix}+\frac{1}{r} e_z\begin{vmatrix} \frac{\partial }{\partial r}&\frac{\partial }{\partial θ}\\ u_r & ru_θ \end{vmatrix}$$
$$=\frac{1}{r} e_rA-e_θ B+\frac{1}{r} e_z C\tag{162}$$
ここで、
$$A=\frac{\partial u_z}{\partial θ}-r\frac{\partial u_θ}{\partial z}\tag{163.a}$$
$$B=\frac{\partial u_z}{\partial r}-\frac{\partial u_r}{\partial z}\tag{163.b}$$
$$C=\frac{\partial }{\partial r}(ru_θ)-\frac{\partial u_r}{\partial θ}=u_θ+r\frac{\partial u_θ}{\partial r}-\frac{\partial u_r}{\partial θ}\tag{163.c}$$
さらに、
$$\mathbf{∇}∧\mathbf{∇}∧\mathbf{u}=e_r∧\frac{\partial }{\partial r}\Bigl(\frac{1}{r} e_rA-e_θ B+\frac{1}{r} e_z C\Bigr)$$
$$+e_θ∧\frac{1}{r}\frac{\partial }{\partial θ}\Bigl(\frac{1}{r} e_rA-e_θ B+\frac{1}{r} e_z C\Bigr)$$
$$+e_z∧\frac{\partial }{\partial z}\Bigl(\frac{1}{r} e_rA-e_θ B+\frac{1}{r} e_z C\Bigr)$$
$$=e_r∧e_r\frac{\partial }{\partial r}\Bigl(\frac{1}{r}A\Bigr)-e_r∧e_θ\frac{\partial }{\partial r}B+e_r∧e_z\frac{\partial }{\partial r}\Bigl(\frac{1}{r}C\Bigr)$$
$$+e_θ∧e_θ\frac{1}{r^2}A+e_θ∧e_r\frac{1}{r^2}\frac{\partial }{\partial θ}A-e_θ∧e_θ\frac{1}{r}\frac{\partial }{\partial θ} B+e_θ∧e_r\frac{1}{r}B+e_θ∧e_z\frac{1}{r^2}\frac{\partial }{\partial θ}C$$
$$+e_z∧e_r\frac{\partial }{\partial z}\Bigl(\frac{1}{r}A\Bigr)-e_z∧e_θ\frac{\partial }{\partial z}B+e_z∧e_z\frac{\partial }{\partial z}\Bigl(\frac{1}{r}C\Bigr)$$
$$=-e_z\frac{\partial }{\partial r}B-e_θ\frac{\partial }{\partial r}\Bigl(\frac{1}{r}C\Bigr)$$
$$-e_z\frac{1}{r^2}\frac{\partial }{\partial θ}A-e_z\frac{1}{r}B+e_r\frac{1}{r^2}\frac{\partial }{\partial θ}C$$
$$+e_θ\frac{1}{r}\frac{\partial }{\partial z}A+e_r\frac{\partial }{\partial z}B$$
$$=e_r\Bigl(\frac{1}{r^2}\frac{\partial }{\partial θ}C+\frac{\partial }{\partial z}B\Bigr)$$
$$-e_θ\Bigl(\frac{\partial }{\partial r}\Bigl(\frac{1}{r}C\Bigr)-\frac{1}{r}\frac{\partial }{\partial z}A\Bigr)\Bigr)$$
$$-e_z\Bigl(\frac{\partial }{\partial r}B+\frac{1}{r^2}\frac{\partial }{\partial θ}A+\frac{1}{r}B\Bigr)\tag{164}$$
上式に式(163)を代入して、
$$\mathbf{∇}∧\mathbf{∇}∧\mathbf{u}=\qquad \qquad \qquad \qquad \qquad \qquad \qquad $$
$$=e_r\Bigl[\frac{1}{r^2}\frac{\partial }{\partial θ}(u_θ+r\frac{\partial u_θ}{\partial r}-\frac{\partial u_r}{\partial θ})+\frac{\partial }{\partial z}(\frac{\partial u_z}{\partial r}-\frac{\partial u_r}{\partial z})\Bigr]$$
$$-e_θ\Bigl[\frac{\partial }{\partial r}(\frac{1}{r}u_θ+\frac{\partial u_θ}{\partial r}-\frac{1}{r}\frac{\partial u_r}{\partial θ})-\frac{1}{r}\frac{\partial }{\partial z}(\frac{\partial u_z}{\partial θ}-r\frac{\partial u_θ}{\partial z})\Bigr]$$
$$-e_z\Bigl[\frac{\partial }{\partial r}(\frac{\partial u_z}{\partial r}-\frac{\partial u_r}{\partial z})+\frac{1}{r^2}\frac{\partial }{\partial θ}(\frac{\partial u_z}{\partial θ}-r\frac{\partial u_θ}{\partial z})+\frac{1}{r}(\frac{\partial u_z}{\partial r}-\frac{\partial u_r}{\partial z})\Bigr]$$
$$=e_r\Bigl[\frac{1}{r^2}\frac{\partial u_θ}{\partial θ}+\frac{1}{r}\frac{\partial^2 u_θ}{\partial r\partial θ}-\frac{1}{r^2}\frac{\partial^2 u_r}{\partial θ^2}+\frac{\partial^2 u_z}{\partial r\partial z}-\frac{\partial^2 u_r}{\partial z^2}\Bigr]$$
$$-e_θ\Bigl[-\frac{1}{r^2}u_θ+\frac{1}{r}\frac{\partial u_θ}{\partial r}+\frac{\partial^2 u_θ}{\partial r^2}+\frac{1}{r^2}\frac{\partial u_r}{\partial θ}-\frac{1}{r}\frac{\partial^2 u_r}{\partial r\partial θ}-\frac{1}{r}\frac{\partial^2 u_z}{\partial θ\partial z}+\frac{\partial^2 u_θ}{\partial z^2}\Bigr]$$
$$-e_z\Bigl[\frac{\partial^2 u_z}{\partial r^2}-\frac{\partial^2 u_r}{\partial r\partial z}+\frac{1}{r^2}\frac{\partial^2 u_z}{\partial θ^2}-\frac{1}{r}\frac{\partial^2 u_θ}{\partial θ\partial z}+\frac{1}{r}\frac{\partial u_z}{\partial r}-\frac{1}{r}\frac{\partial u_r}{\partial z}\Bigr]\tag{165}$$
したがって、\(\mathbf{∇}^2\mathbf{u}\)は式(160)から式(165)を引くことで求められる。単位ベクトル毎にまとめると、
$$e_r項:\qquad \frac{\partial }{\partial r}\Bigl[\frac{u_r}{r}+\frac{\partial u_r}{\partial r}+\frac{1}{r}\frac{\partial u_θ}{\partial θ}+\frac{\partial u_z}{\partial z}\Bigr]\qquad \qquad \qquad \qquad \qquad $$
$$-\Bigl[\frac{1}{r^2}\frac{\partial u_θ}{\partial θ}+\frac{1}{r}\frac{\partial^2 u_θ}{\partial r\partial θ}-\frac{1}{r^2}\frac{\partial^2 u_r}{\partial θ^2}+\frac{\partial^2 u_z}{\partial r\partial z}-\frac{\partial^2 u_r}{\partial z^2}\Bigr]$$
$$=-\frac{1}{r^2}u_r+\frac{1}{r}\frac{\partial u_r}{\partial r}+\frac{\partial^2 u_r}{\partial r^2}-\frac{1}{r^2}\frac{\partial u_θ}{\partial θ}+\frac{1}{r}\frac{\partial^2 u_θ}{\partial r\partial θ}+\frac{\partial u^2_z}{\partial r\partial z}$$
$$-\frac{1}{r^2}\frac{\partial u_θ}{\partial θ}-\frac{1}{r}\frac{\partial^2 u_θ}{\partial r\partial θ}+\frac{1}{r^2}\frac{\partial^2 u_r}{\partial θ^2}-\frac{\partial^2 u_z}{\partial r\partial z}+\frac{\partial^2 u_r}{\partial z^2}$$
$$=\Bigl(\frac{\partial^2 }{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{1}{r^2}\frac{\partial^2 }{\partial θ^2}+\frac{\partial^2 }{\partial z^2}\Bigr)u_r-\frac{1}{r^2}\Bigl(u_r+2\frac{\partial u_θ}{\partial θ}\Bigr)\tag{166.a}$$
$$e_θ項:\qquad \frac{1}{r}\frac{\partial }{\partial θ}\Bigl[\frac{u_r}{r}+\frac{\partial u_r}{\partial r}+\frac{1}{r}\frac{\partial u_θ}{\partial θ}+\frac{\partial u_z}{\partial z}\Bigr]\qquad \qquad \qquad \qquad \qquad $$
$$+\Bigl[-\frac{1}{r^2}u_θ+\frac{1}{r}\frac{\partial u_θ}{\partial r}+\frac{\partial^2 u_θ}{\partial r^2}+\frac{1}{r^2}\frac{\partial u_r}{\partial θ}-\frac{1}{r}\frac{\partial^2 u_r}{\partial r\partial θ}-\frac{1}{r}\frac{\partial^2 u_z}{\partial θ\partial z}+\frac{\partial^2 u_θ}{\partial z^2}\Bigr]$$
$$=\frac{1}{r^2}\frac{\partial u_r}{\partial θ}+\frac{1}{r}\frac{\partial^2 u_r}{\partial r\partial θ}+\frac{1}{r^2}\frac{\partial^2 u_θ}{\partial θ^2}+\frac{1}{r}\frac{\partial^2 u_z}{\partial θ\partial z}$$
$$-\frac{1}{r^2}u_θ+\frac{1}{r}\frac{\partial u_θ}{\partial r}+\frac{\partial^2 u_θ}{\partial r^2}+\frac{1}{r^2}\frac{\partial u_r}{\partial θ}-\frac{1}{r}\frac{\partial^2 u_r}{\partial r\partial θ}-\frac{1}{r}\frac{\partial^2 u_z}{\partial θ\partial z}+\frac{\partial^2 u_θ}{\partial z^2}$$
$$=\Bigl(\frac{\partial^2 }{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{1}{r^2}\frac{\partial^2 }{\partial θ^2}+\frac{\partial^2 }{\partial z^2}\Bigr)u_θ-\frac{1}{r^2}\Bigl(u_θ-2\frac{\partial u_r}{\partial θ}\Bigr)\tag{166.b}$$
$$e_z項:\qquad \frac{\partial }{\partial z}\Bigl[\frac{u_r}{r}+\frac{\partial u_r}{\partial r}+\frac{1}{r}\frac{\partial u_θ}{\partial θ}+\frac{\partial u_z}{\partial z}\Bigr]\qquad \qquad \qquad \qquad \qquad $$
$$+\Bigl[\frac{\partial^2 u_z}{\partial r^2}-\frac{\partial^2 u_r}{\partial r\partial z}+\frac{1}{r^2}\frac{\partial^2 u_z}{\partial θ^2}-\frac{1}{r}\frac{\partial^2 u_θ}{\partial θ\partial z}+\frac{1}{r}\frac{\partial u_z}{\partial r}-\frac{1}{r}\frac{\partial u_r}{\partial z}\Bigr]$$
$$=\frac{1}{r}\frac{\partial u_r}{\partial z}+\frac{\partial^2 u_r}{\partial r\partial z}+\frac{1}{r}\frac{\partial^2 u_θ}{\partial θ\partial z}+\frac{\partial^2 u_z}{\partial z^2}$$
$$+\frac{\partial^2 u_z}{\partial r^2}-\frac{\partial^2 u_r}{\partial r\partial z}+\frac{1}{r^2}\frac{\partial^2 u_z}{\partial θ^2}-\frac{1}{r}\frac{\partial^2 u_θ}{\partial θ\partial z}+\frac{1}{r}\frac{\partial u_z}{\partial r}-\frac{1}{r}\frac{\partial u_r}{\partial z}$$
$$=\Bigl(\frac{\partial^2 }{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{1}{r^2}\frac{\partial^2 }{\partial θ^2}+\frac{\partial^2 }{\partial z^2}\Bigr)u_z\tag{166.c}$$
円筒座標系のNavier式
円筒座標系のNavier式は、式(151)に式(160)と式(166.a~c)を代入して得られます。単位ベクトル毎にまとめると、
$$μ\Bigl[\mathbf{∇}^2u_r-\frac{1}{r^2}\Bigl(u_r+2\frac{\partial u_θ}{\partial θ}\Bigr)\Bigr]+(λ+μ)\frac{\partial }{\partial r}(\mathbf{∇}・\mathbf{u})=ρ\ddot{u_r}\tag{167.a}$$
$$μ\Bigl[\mathbf{∇}^2u_θ-\frac{1}{r^2}\Bigl(u_θ-2\frac{\partial u_r}{\partial θ}\Bigr)\Bigr]+(λ+μ)\frac{1}{r}\frac{\partial }{\partial θ}(\mathbf{∇}・\mathbf{u})=ρ\ddot{u_θ}\tag{167.b}$$
$$μ\mathbf{∇}^2u_z+(λ+μ)\frac{\partial }{\partial z}(\mathbf{∇}・\mathbf{u})=ρ\ddot{u_z}\tag{167.c}$$
ここで、ラプラシアンは式(136)(線形弾性理論12参照)、ダイバージェンスは式(159)のように求められています。ラプラシアンとダイバージェンスを再度記載すると、
$$\mathbf{∇}^2=\frac{\partial^2}{\partial r^2}+\frac{1}{r}\frac{\partial}{\partial r}+\frac{1}{r^2}\frac{\partial^2}{\partial θ^2}+\frac{\partial^2}{\partial z^2}\tag{136}$$
$$\mathbf{∇・u}=\frac{u_r}{r}+\frac{\partial u_r}{\partial r}+\frac{1}{r}\frac{\partial u_θ}{\partial θ}+\frac{\partial u_z}{\partial z}\tag{159}$$
以上です。


コメント