円筒座標系の波動方程式を解くときに、第一種ベッセル関数を用います。ExcelVBAで計算を行う場合にはExcelの組み込み関数が用意されていますが、適用限界や精度に問題が無いか不安が残ります。そこで、級数展開と漸近式からの計算結果と組み込み関数を比較して検証を行います。結果として、ここで検証した範囲では組み込み関数で問題ないことが分りました。
ベッセル関数とは
ベッセル関数は、つぎのベッセルの微分方程式における \(y(x)\) の特殊解のひとつだそうです。
$$x^2\frac{d^2y}{dx^2}+x\frac{dy}{dx}+(x^2-α^2)y=0\tag{1}$$
\(α\)は整数の時に次数と呼ばれます。
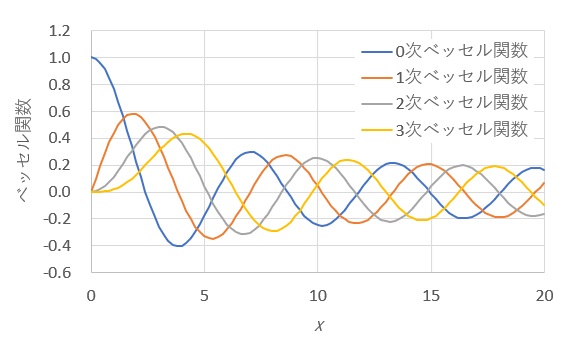
円筒座標系での波動方程式では、半径方向にハンケル変換を用いて波数領域に変換しますが、その際に0次や1次の第一種ベッセル関数を利用することになります。グラフに描くとつぎのような関数です。
Excelの組み込み関数
Excelの組み込み関数”BESSELJ(xの値,ベッセル次数)”を使うのが便利です。ExcelVBAのプロシージャ上では、つぎのように指定します。
=WorksheetFunction.BesselJ(x, n)
さて、この組み込み関数が本当に欲しい値を与えているのかを、検証していきます。
x=0近辺のべき級数
x=0でのテイラー展開をすると次式のようになるそうですので、ExcelVBAで収束値を計算して、組み込み関数と比較します。
$$J_n(x)=\sum_{m=0}^{∞}\frac{(-1)^m}{m!(m+n)!}\Bigl(\frac{x}{2}\Bigr)^{2m+n}\tag{2}$$
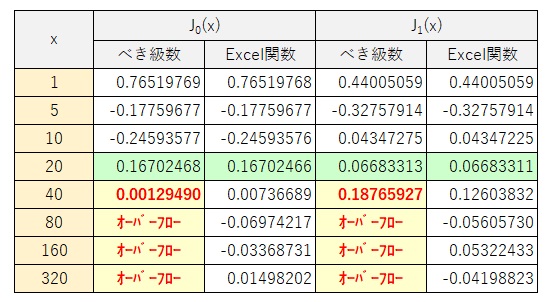
\(x\) の \(2m+n\) 乗を計算していきますので、\(x\) が大きくなるとオーバーフローを起こしてしまいます。しかし、\(x=20\) までを比較すると、組み込み関数はほぼ問題のない精度で計算できていることがわかります。
参考にVBAの計算部分を掲載しますが、xをDx*iとしていますのでメインでiを引き渡してください。また、上表の値になる以外は保証がありませんのでご了承ください。
'**************************************************
' n :ベッセル次数 , Dx :xの刻み距離Δx
' Nm :級数項の最大回数 , Nx :xの個数
' Jn() :ベッセル関数の直 , Jns :前ステップのJn()
' keisu:係数 ,xkou():xの項or xの値
' ER :誤差
'**************************************************
Dim n As Long, Nm As Long, Nx As Long, i As Long, j As Long
Dim xkou(10000) As Double, Jn(10000) As Double
Dim keisu As Double, Dx As Double, ER As Double, Jns As Double
Sub Xshou()
keisu = 1 / kaijou(n)
xkou(i) = (Dx * i / 2) ^ n
Jn(i) = keisu * xkou(i)
Jns = Jn(i)
ER = 10
j = 1
Do While ER > 0.00000001 And j < Nm
keisu = keisu * (-1) / j / (j + n)
xkou(i) = xkou(i) * (Dx * i / 2) ^ 2
Jn(i) = Jn(i) + keisu * xkou(i)
ER = Abs((Jns - Jn(i)) / Jns)
Jns = Jn(i)
j = j + 1
Loop
End Sub
Function kaijou(n As Long) As Double
Dim k As Long
kaijou = n
If n <= 1 Then
kaijou = 1
Else
kaijou = n * kaijou(n - 1)
End If
End Function
漸近式の計算
つぎに、\(x\) が大きくなったときの精度を検証するために、つぎの漸近式を用いて検証します。
$$J_n(x)=\sqrt{\frac{2}{πx}}\biggl[A_n(x)cos\Bigl(x-\frac{2n+1}{4}π\Bigr)-B_n(x)sin\Bigl(x-\frac{2n+1}{4}π\Bigr)\biggr] \tag{3}$$
$$A_n(x)=\sum_{k=0}^{∞}(-1)^k\frac{(n,2k)}{(2x)^{2k}} , B_n(x)=\sum_{k=0}^{∞}(-1)^k\frac{(n,2k+1)}{(2x)^{2k+1}} \tag{4}$$
ここで、
$$(n,j)=\frac{(n+j-\frac{1}{2})(n+j-\frac{3}{2})・・・(n-j+\frac{1}{2})}{j!} \tag{5.a}$$
$$(n,0)=1\tag{5.b}$$
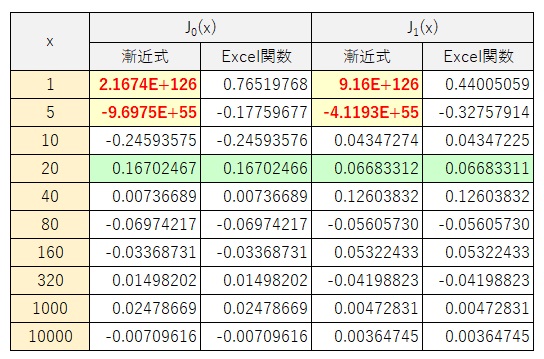
上式から \(x\) が \(0\) に近づくと発散していくことが分ります。 \(x>20\) では組み込み関数はほぼ問題のない精度で計算できていることがわかります。
参考にVBAの計算部分を掲載しますが、xをxkou(i)=Dx*iとしてメインから引き渡しています。また、上表の値になる以外は保証がありませんのでご了承ください。
'**************************************************
' n :ベッセル次数 , Dx :xの刻み距離Δx
' Nm :級数項の最大回数
' Jn() :ベッセル関数の直 , Jns :前ステップのJn()
' xkou():xの項or xの値 , X2 :2x
' ER :誤差 , C :√係数
' Sita :sin、cos内数値 , a1,b1:A,Bの各項
' asum,bsum:a1とb1項の合計(A,B)
'**************************************************
Dim n As Long, Nm As Long, i As Long, j As Long
Dim xkou(10000) As Double, Jn(10000) As Double
Dim Dx As Double, ER As Double, Jns As Double
Dim X2 As Double, C As Double, Sita As Double, pi As Double
Dim a1 As Double, b1 As Double, asum As Double, bsum As Double
Sub Xdai()
X2 = 2# * xkou(i)
C = (2# / xkou(i) / pi) ^ 0.5
Sita = xkou(i) - (2 * n + 1) / 4 * pi
a1 = 1#
b1 = (n + 0.5) * (n - 0.5) / X2
asum = a1
bsum = b1
Jns = C * (asum * Cos(Sita) - bsum * Sin(Sita))
ER = 10
j = 1
Do While ER > 0.00000001 And j < Nm
j = j + 1
a1 = -(n + j - 0.5) * (n - j + 0.5) / j / X2 * b1
j = j + 1
b1 = (n + j - 0.5) * (n - j + 0.5) / j / X2 * a1
asum = asum + a1
bsum = bsum + b1
Jn(i) = C * (asum * Cos(Sita) - bsum * Sin(Sita))
ER = Abs((Jns - Jn(i)) / Jns)
Jns = Jn(i)
Loop
End Sub


コメント