ここでは、ExcelVBAでモンテカルロシミュレーション【滑動に関する信頼性解析】とPythonでモンテカルロシミュレーション【滑動に関する信頼性解析】に示した滑動の例題をFORM(First-Order Reliability Method)により算定します。Excel上で信頼性指標が収束するまで計算を繰り返し、破壊確率を求めます。
FORMの定式化
性能関数\(Z\)を変数 \( X_1, X_2 ,・・・, X_n \) に関して、破壊点 \( ( X_1^*, X_2^* ,・・・, X_n^* ) \) まわりでテーラー展開を行い、1回微分までの項で近似します。
$$Z=g(X_1^*, X_2^* ,・・・, X_n^* )+\sum_{j=1}^n\big(\mu_{\small X_j}- X_j^* \big)\frac{\partial g}{\partial X_j}\bigg|_{X^*} \tag{1} $$
\(Z\) の平均値\( \mu_{z} \)および標準偏差 \( \sigma_{z} \) は、以下のように与えられます。
$$ \mu_{z} =g(X_1^*, X_2^* ,・・・, X_n^* )+\sum_{j=1}^n\big(\mu_{\small X_j}- X_j^* \big)\frac{\partial g}{\partial X_j}\bigg|_{X^*} \tag{2} $$
$$ \sigma_{z} =\sum_{j=1}^n\alpha_j\big(\frac{\partial g}{\partial X_j}\bigg|_{X^*}\big) \sigma_{\small X_j} \tag{3} $$
これを用いて、信頼性指標 \(\beta\) が計算できます。
$$\beta= \frac{ \mu_{z} }{ \sigma_{z} } \tag{4} $$
このとき、破壊点 \( X^* = ( X_1^* , X_2^* ,・・・, X_n^* ) \) に関して次の3式が成り立ちます。
$$g(X_1^*, X_2^* ,・・・, X_n^* )=0 \tag{5} $$
$$ X^* =\mu_{\small X_j}- \alpha_j \frac{ \mu_{z} }{ \sigma_{z} } \sigma_{ \small X_j }: j=1,2,・・・,n \tag{6} $$
$$ \alpha_{j} =\frac{\big(\frac{\partial g}{\partial X_j}\big|_{X^*}\big) \sigma_{\small X_j}}{\Biggl\{\sum_{j=1}^{n} \bigg(\frac{\partial g}{\partial X_j}\big|_{X^*}\bigg)^2 \sigma_{\small X_j}^2 \Biggr\}^\frac{1}{2}} \tag{7} $$
滑動の例題
滑動の例題は下図のようです。

性能関数 \(Z\) および\(g\)の偏微分は、それぞれ以下のようです。
$$ Z=g(X_1,X_2,X_3)= X_1・X_3-X_2 \tag{8} $$
$$ \frac{\partial g}{\partial X_1}= X_3, \frac{\partial g}{\partial X_2}= -1 , \frac{\partial g}{\partial X_3}= X_1 \tag{9} $$
Excelでの計算方法
計算フローを以下に示します。
- 初期値として、\(\alpha_1= \alpha_2 = \alpha_3 =\sqrt{1/n}= \sqrt{1/3} \) , \(\beta=2 \)と仮定
- 式(6)より、 \(X_1^*, X_2^* , X_3^* \) を計算( \(\frac{ \mu_{z} }{ \sigma_{z} } = \beta \) )
- 式(9)より、\( \frac{\partial g}{\partial X_1}\big|_{X^*} \), \( \frac{\partial g}{\partial X_2}\big|_{X^*} \) , \( \frac{\partial g}{\partial X_3}\big|_{X^*} \) を計算
- 式(7)の分母を計算(これが\( \sigma_{z} \)であり、式(3)と同じ値となる)
- これらを式(7)に代入して \(\alpha_1, \alpha_2 , \alpha_3 \) を計算
- 平均値 \( \mu_{z} \) を式(2)より算定
- 標準偏差\( \sigma_{z} \) を式(3)より算定
- 信頼性指標 \(\beta\) を式(4)より算定
- 2.~8.を繰り返し、 \(\beta\) が収束したら、標準正規分布の累積分布関数の値NORMSDIST(\(-\beta\) )より破壊確率を計算する
Excelでの計算結果を示します。F列以降はE列の計算式をコピーしていくだけです。
なお、式(7)の分母と式(3)からそれぞれ求めた \( \sigma_{z} \) は、 \(\alpha_j \)の定義から 同じ値となるのは明らかですが、同値になることを確認しています。
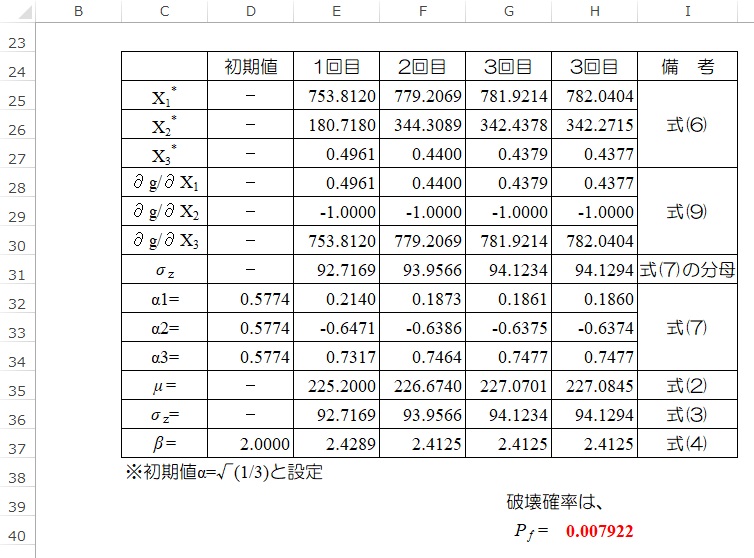
FORMによる計算のまとめ
FORM (First-Order Reliability Method)は多次元空間における多重積分問題を2次元問題に近似し、性能関数がゼロとなる座標のうち、同時確率密度が最も高い点(設計点( design point ))を見つける方法です。互いに独立な標準正規確率変数の空間へ変換すると、原点から最も近い点として 設計点(design point)が求められます。また、設計点(design point)において求められるβは、性能関数によらず一定値になります。
性能関数の破壊点周りの線形化近似を用いている点に適用の注意は必要ですが、Excelで簡単に計算が可能です。



コメント