前回は一次元非線形連続力学の運動の表示、変形、時間変化率について示しました。今回は、質量保存、運動量のつり合い、エネルギーのつり合いについて示します。
質量保存
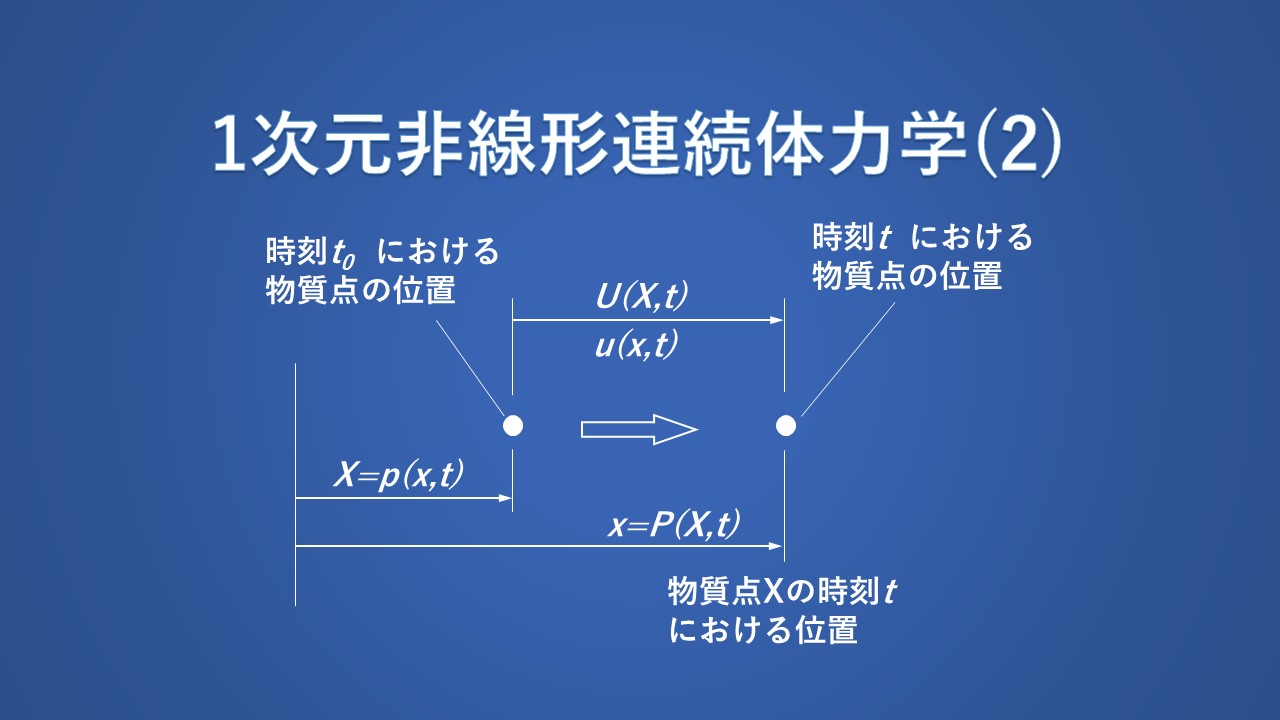
古典力学の基本原理の 1 つは、物質は創造も破壊もできないということです。固定された空間領域 \(x_1≦x≦x_2\) を瞬間的に占有する質量系を考えてみましょう。空間記述における位置 \(x\) および時間 \(t\) での質量密度を \(ρ(x,t)\) とし、基準配置の関数としての質量密度を \(ρ_0(X)\) とします。したがって、質量保存は次のことを意味します。
$$\int_{x_1} ^ {x_2} ρ(x,t)dx=\int_{p(x_1,t)} ^ {p(x_2,t)} ρ_0(X)dX$$
ここで、 \(ρ(x,t)\) は式(2)で定義されていますが、上式の左辺に式(1)を使用して変数の変換を実行します。その結果、 \(ρ_0(X)\) と \(ρ(x,t)\) は次のように関係付けられることがわかります。
$$ρ_0(X)=ρ(x,t)\frac{\partial P(X,t)}{\partial X}\tag{15}$$
質量保存の法則は、粒子系の質量の時間変化率が発生しないことも意味します。したがって、粒子が空間領域 \(x_1≦x≦x_2\) を瞬間的に占有する場合、
$$\frac{d}{dt}\int_{x_1} ^ {x_2} ρ(x,t)dx=0$$
上式に式(14)を適用すると、次の結果が得られます。
$$\frac{\partial ρ}{\partial t}+\frac{\partial}{\partial t}(ρv)=0\tag{16}$$
この方程式は、空間表示における質量保存を表します。
式(16)は、質量密度と別の関数との積に関する積分の物質導関数を簡略化するために便利に使用できます。輸送定理式(14)によれば、次のように書くことができます。
$$\frac{d}{dt}\int_{x_1} ^ {x_2} ρfdx=\int_{x_1} ^ {x_2} \biggl[\frac{\partial}{\partial t}(ρf)+\frac{\partial}{\partial x}(ρfv)\biggr]dx$$
右辺は式(16)を使用して簡略化でき、次のようになります。
$$\frac{d}{dt}\int_{x_1} ^ {x_2} ρfdx=\int_{x_1} ^ {x_2} ρ\frac{Df}{Dt}dx\tag{17}$$
ここで \(D/Dt\) は式(10)で示した偏微分を表します。この結果は、運動量とエネルギーのバランスについての議論に役立つことがわかります。
運動量のつり合い
線形運動量の平衡原理は、システムの線形運動量の瞬間的な変化率が、システムに作用する合成外力に等しいとする原理です。 \(x_1≦x≦x_2\) の領域に瞬間的に位置する単位断面積の質量系を考えると、原理は次のことを意味します。
$$τ(x,t)|_{x=x_1} ^ {x=x_2}=\frac{d}{dt}\int_{x_1} ^ {x_2} ρ(x,t)v(x,t)dx\tag{18}$$
ここで、 \(t\) は点 \(x\) における空間表示の応力を定義し、物体からの力は考慮されません。左辺を積分表示し、右辺を式(17)で簡略化すると、方程式は次のように書き直すことができます。
$$\int_{x_1} ^ {x_2} \frac{\partial τ}{\partial x}dx=\int_{x_1} ^ {x_2}ρ(x,t)\frac{Dv}{Dt}dx\tag{19}$$
明らかに、式(19)は次式と等価です。
$$\frac{\partial τ}{\partial x}=ρ\frac{Dv}{Dt}\tag{20}$$
これは空間座標における運動方程式です。物質座標の運動方程式を決定するには、式(18)に戻り、マッピング式(1)によって座標の変更を導入します。 \(ρ_0(X)\) と \(ρ(x,t)\) の関係を使用して、次の関係が得られます。
$$\frac{\partial T}{\partial X}=ρ_0\frac{\partial v}{\partial t}\tag{21}$$
ここで、 \(T(X,t)=τ[P(X,t),t]\) は物質表示での応力です。
運動の応力方程式は、応力と変形の関係によって説明されます。理想的な弾性体の場合、応力は変形に適切な処置がされた関数として表されます。1 次元では、物質表示の応力 \(T(X,t)\) を変位勾配 \(\partial U/\partial X\) の関数として考慮すると便利です。
$$T(X,t)=φ(\partial U/\partial X)\tag{22}$$
物質表示の運動方程式は次のように書くことができます。
$$C^2\frac{\partial^2 U}{\partial X^2}=\partial^2 U/\partial t^2\tag{23}$$
ここに、
$$C^2=\frac{1}{ρ_0}\frac{dφ}{d(\partial U/\partial X)}\tag{24}$$
エネルギーの釣り合い
エネルギー保存の原理は、質量系の運動エネルギーと内部エネルギーの合計の時間変化率は、外部より加えられた力の仕事率と単位時間当たりに系に出入りする他のすべてのエネルギーを加えたものに等しいという原理です。
単位質量当たりのある瞬間のエネルギーを \(e(x,t)\) で表すと、領域 \(x_1≦x≦x_2\) に含まれる内部エネルギーは、
$$\int_{x_1} ^ {x_2} ρe(x,t)dx$$
ある瞬間の運動エネルギーは、
$$\frac{1}{2}\int_{x_1} ^ {x_2} ρv^2dx$$
応力は、メカニカルな仕事の形でエネルギーをシステムに伝達します。仕事率は動力投入量 \(P\) と呼ばれ、
$$P=-τ(x_1,t)v(x_1,t)+τ(x_2,t)v(x_2,t)=\int_{x_1} ^ {x_2} \frac{\partial }{\partial x}(τv)dx\tag{25}$$
この式では、物体からの力は考慮されていません。
エネルギーは、伝導や連続体の内部に分布する熱源によって、熱の形で伝達されることもありま す。ただし、この段階では熱の影響は考慮されません。
純粋にメカニカルなシステムの場合、エネルギー保存則は次のように表すことができます。
$$P=\frac{d}{dt}\int_{x_1} ^ {x_2}ρedx+ \frac{d}{dt}\int_{x_1} ^ {x_2}\frac{1}{2}ρv^2dx\tag{26}$$
右辺の積分は式(17)を適用することで評価できます。また、運動方程式(20)を使用すると、次のことがわかります。
$$ρ\frac{De}{Dt}=τ\frac{\partial v}{\partial x}\tag{27}$$
以上、質量保存、運動量のつり合い、エネルギーのつり合いについて示しました。次回は、線形一次元波動方程式を導きます。

コメント