前回までに示した衝撃載荷による一様成層地盤の変位解より求めた、波数領域でのモードの伝達関数を示します。ここで示す結果は、Excel VBAにより計算をした結果であり、Fortran等よりも精度に問題はあるものの、実用的な解を得ることが出来ています。
波数領域でのモードの伝達関数
前回の【衝撃載荷による一様成層地盤の波動伝播特性4】で示した式(52)~式(54)中の \(\{ϕ_{ij}・T(p_{i}t)・\tilde{Φ}_{jn}\}\) は波数領域での各モードの寄与率を与えるものであると理解できる。ここでは、それぞれのフーリエ変位振幅成分に含まれる関数 \(μξ\{ϕ_{ij}・T(p_{i}t)・\tilde{Φ}_{jn}\}/f_{j}\) を波数領域での各モードの伝達関数として定義し、以下に考察を行う。
なお、以下に示す伝達関数は、時間関数にヘヴィサイド関数を用い、ポアソン比 \(ν=0.3\) の地盤に対して数値計算されたものである。
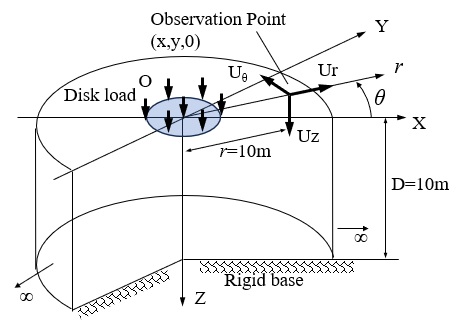
地表面点載荷
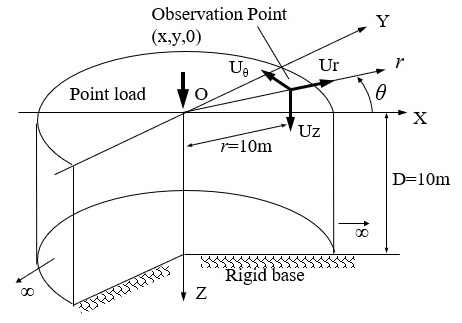
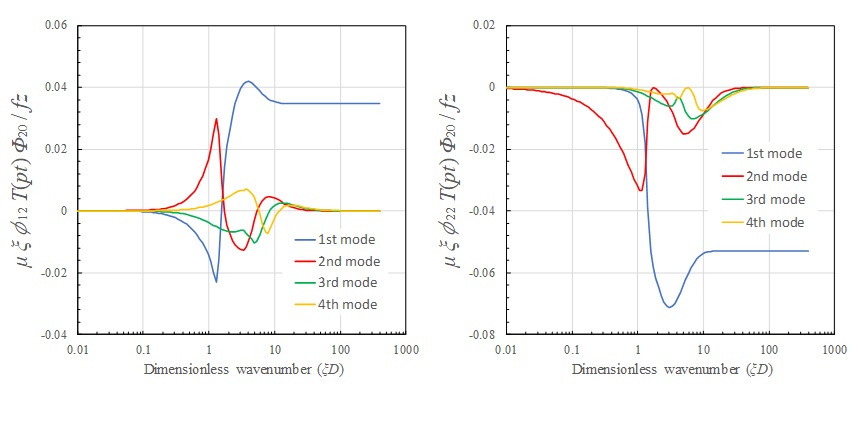
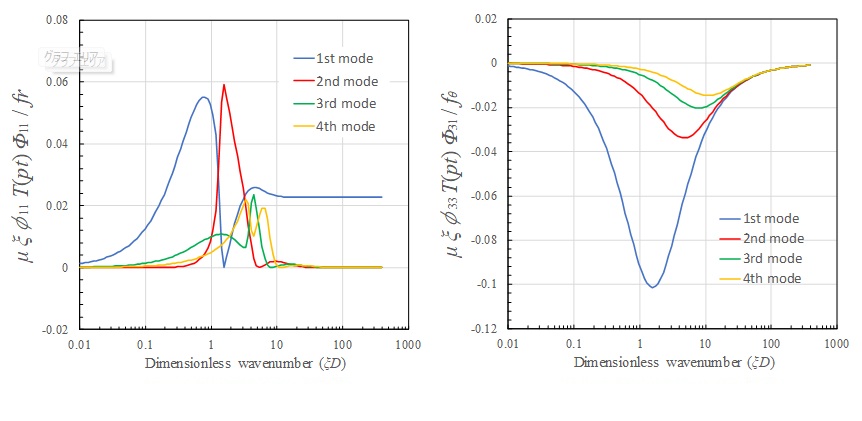
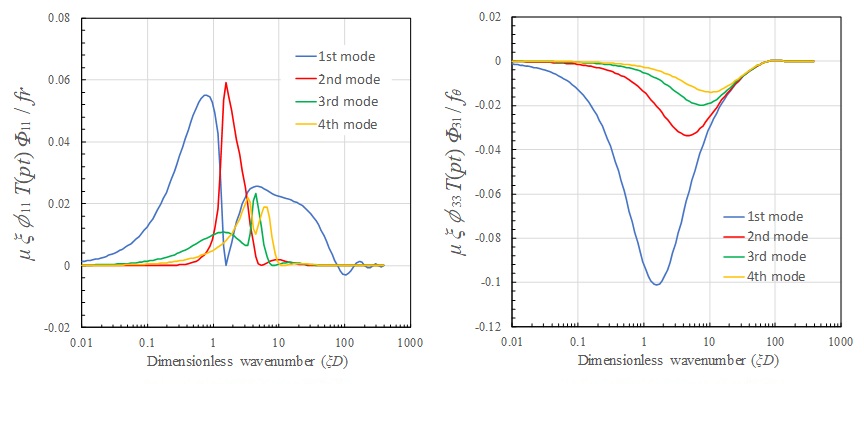
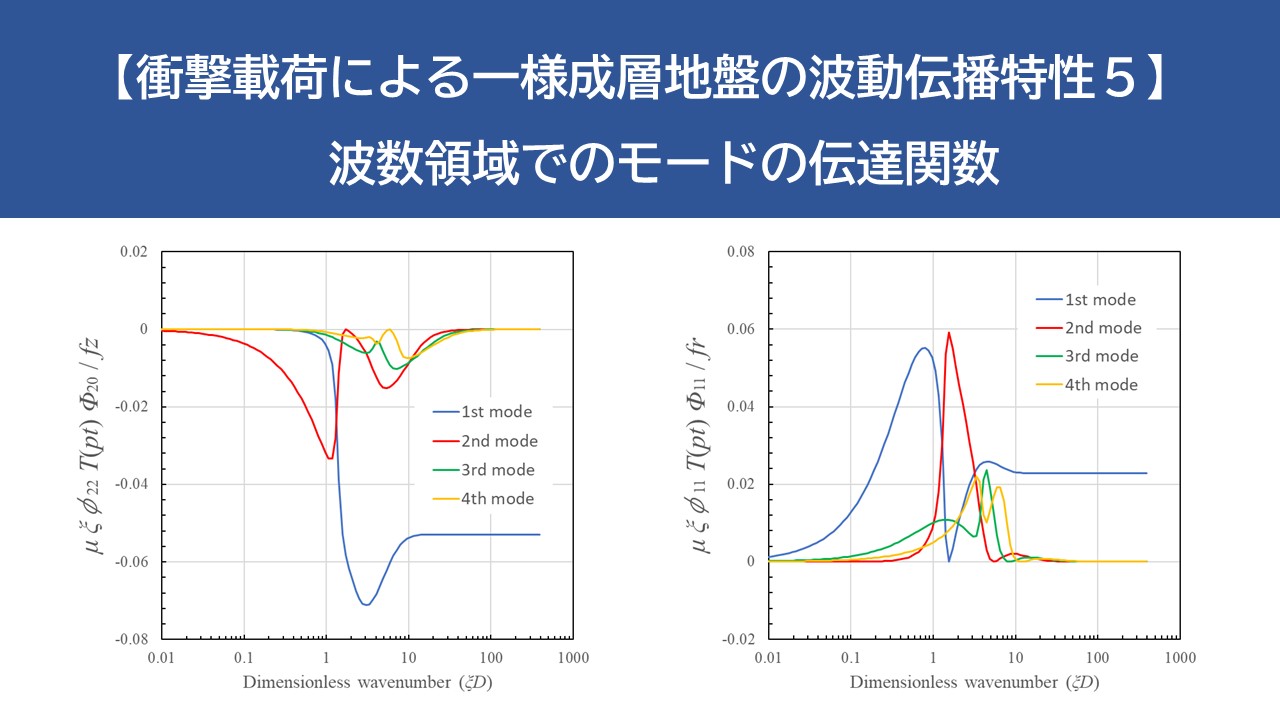
下図は地表面上に点載荷が作用した場合の地表面上の伝達関数である。いずれの成分においても1次モードの寄与が高く、高次になるほど寄与が小さくなっていく傾向にある。その波数域は、低次モードほど小さく、高次になるほど上がり、各モードの卓越波数域は【衝撃載荷による一様成層地盤の波動伝播特性4】で示したAiry相に一致する。
また、Z方向載荷およびr方向載荷では \(ξD>10\) の波数領域では1次モードが支配的となっており、地表面載荷の地表面応答ではRayleigh波成分が卓越することが分かる。
波数積分は、これらの伝達関数とベッセル関数で表わされる観測点までの距離の関数との積に対して遂行される。従って、載荷点から観測点までの距離が長い場合には同波数領域でのモードの寄与が下がり数値積分が可能であるが、点載荷近傍では解の収束性は保証されない。
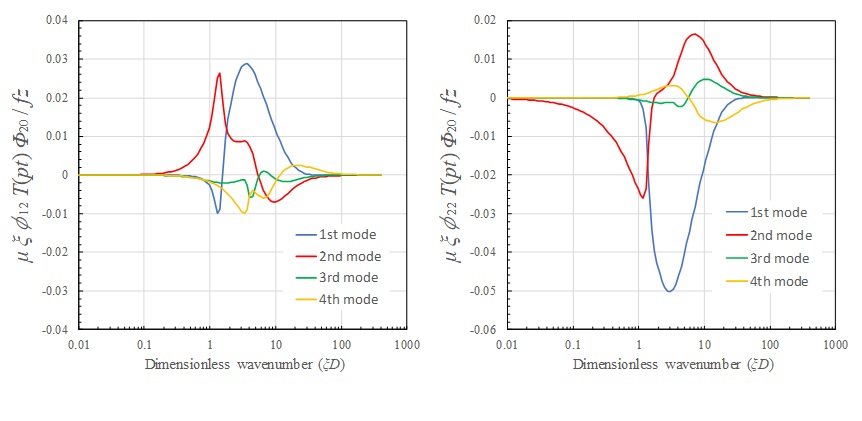
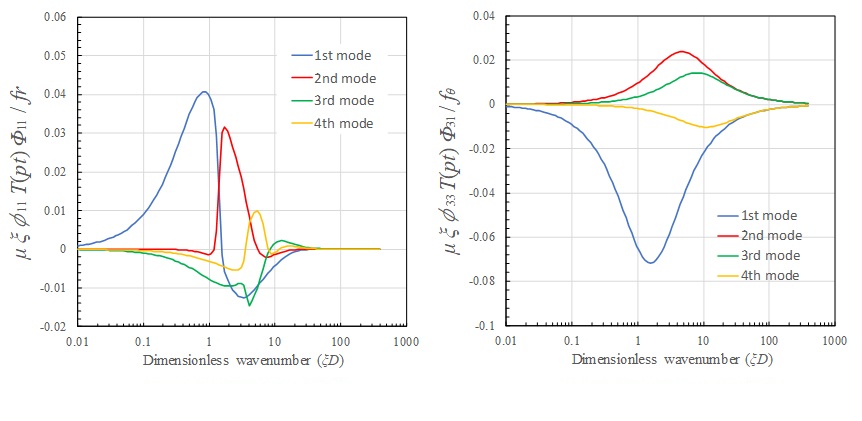
地中点載荷
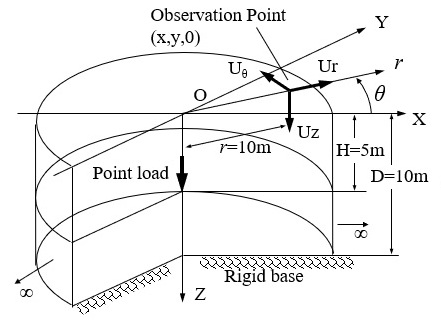
同じ点載荷について、層厚の半分 \(D/2\) の深さに地中載荷した場合の地表面の伝達関数を示す。地中載荷の場合も地表面載荷と同様に1次モードの寄与が高く、高次になるほど寄与が小さくなっていく傾向にあり、その波数域は各モードのAiry相に一致する。しかし、 \(ξD>10\) の波数領域での1次モードの寄与が消え、高次モードになるほど大きな波数域での寄与が高くなっている。従って、地中載荷では、地表面点載荷に比べれば解の収束性が良いと言えるものの、高次モードに対する解の収束性には問題がある。
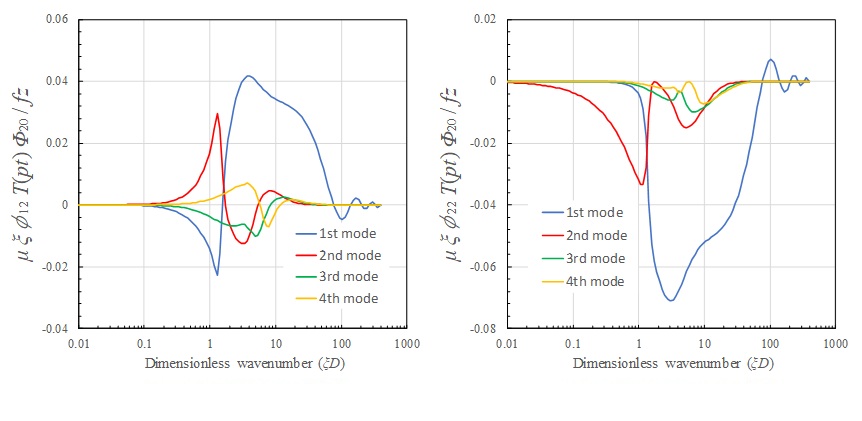
地表面ディスク載荷
地表面上に半径 \(r_{d}=0.5m\) のディスク載荷を行った場合の地表面上での伝達関数を示す。いずれの載荷方向に関しても【衝撃載荷による一様成層地盤の波動伝播特性3】に示した波数領域のディスク載荷の性質から、高い波数領域での伝達関数が制限されていることが分かる。ディスク半径が大きいほどこの性質は強まり、波数積分による解の収束性が保証される。現実問題での載荷状態は、完全な点載荷よりもむしろある程度の載荷面積を持つと考えられることや、ディスク半径のおおよそ7倍以上の距離での変位応答は点載荷と差が無くなると言われていることからも、載荷状態をディスク載荷でモデル化することの適用範囲は広いと言える。
Excel VBAでの計算
今回の計算もExcel VBAを使いましたが、Fortranのように複素数の演算子が無いために、かなり苦労をしました。また、変数は倍精度としていますが、波数が大きくなると発散する傾向が強くなるために、適時 \(ξ^{6}\) や \(exp()\) 等で条件式を割るなどの工夫を行いました。演算時間はある程度時間を要しますが、十分な精度の演算が可能であったと思います。
30年ほど前に大型計算機で数時間の演算時間を要していたことを考えると、一般に市販されているパソコンのExcelで数十分で計算ができたことから、ハードの進歩は凄まじいものであると実感させられました。


コメント