数学的に考えられるすべての関数ではありませんが、物理的現象を表わす関数として級数(各項の集合に分割)で表現できることはよく知られています。一般的な級数として、各項が正弦関数または虚数指数を含む指数関数で表わされるものがあります。関数が周期 \(T\) および周波数 \(ω=2π/T\) で周期的に繰り返される場合、周波数(角振動数) \(ω,2ω,・・・・\) をもつ \(cos\) 項と \(sin\) 項のフーリエ級数として表すことができます。また、外力が周期的でない場合は、正弦波または指数項にわたるフーリエ積分として表すことができます。ここでは、フーリエ級数とフーリエ積分による表現の重要な側面を簡単にまとめます。
フーリエ級数
関数の値が間隔 \(T\) で繰り返される場合、その関数は時間的に周期的であり、周期 \(T\) としたときに \(f(t+T)=f(t)\) と表わされます。ある周期関数を図に示しますが、関数は空間内で周期的な長さ (波長) \(Λ\) 、つまり \(f(x+Λ)=f(x)\) で周期的になることがあります。
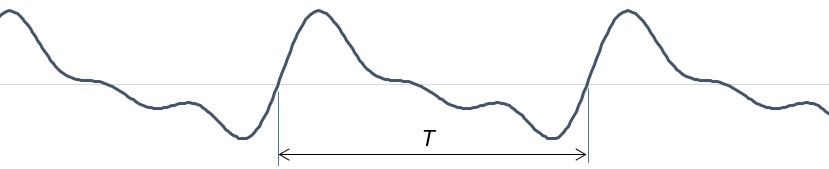
近似的に周期 \(T\) の周期関数はフーリエ級数で表すことができます。
$$f(t)=\frac{1}{2}a_0+\sum_{n=1}^∞\Bigl[a_n\enspace cos\Bigl(\frac{2πnt}{T}\Bigr)+b_n\enspace sin\Bigl(\frac{2πnt}{T}\Bigr)\Bigr]\tag{92}$$
この級数が収束して \(f(t)\) に収束する条件を決定することは、決して簡単な問題ではありません。ただし、 \(f(t)\) とその一次導関数が、各期間内の微小な不連続点を除いて連続である場合、この条件は満たされます。また、関数が滑らかであればあるほど、級数はより早く収束します。
つぎの \(sin\) 関数と \(cos\) 関数の直交性を利用すると、フーリエ級数の各係数が得られます。
$$\int_{-\frac{1}{2}T}^{\frac{1}{2}T}\enspace cos\Bigl(\frac{2πnt}{T}\Bigr)\enspace cos\Bigl(\frac{2πmt}{T}\Bigr)\enspace dt=\frac{1}{2}Tδ_{nm}$$
$$\int_{-\frac{1}{2}T}^{\frac{1}{2}T}\enspace sin\Bigl(\frac{2πnt}{T}\Bigr)\enspace sin\Bigl(\frac{2πmt}{T}\Bigr)\enspace dt=\frac{1}{2}Tδ_{nm}$$
$$\int_{-\frac{1}{2}T}^{\frac{1}{2}T}\enspace cos\Bigl(\frac{2πnt}{T}\Bigr)\enspace sin\Bigl(\frac{2πmt}{T}\Bigr)\enspace dt=0\enspace \enspace \enspace n≧0,m≧0$$
クロネッカーデルタ \(δ_{mn}\) は、 \(n=m\) のとき1、 \(n≠m\) のとき0を表します。この関係から式(92)に \(sin\) 関数あるいは \(cos\) 関数をかけて周期分の積分を行うと、次の関係が得られます。
$$a_n=\frac{2}{T}\int_{-\frac{1}{2}T}^{\frac{1}{2}T}\enspace f(t)\enspace cos\Bigl(\frac{2πnt}{T}\Bigr)\enspace dt\tag{93}$$
$$b_n=\frac{2}{T}\int_{-\frac{1}{2}T}^{\frac{1}{2}T}\enspace f(t)\enspace sin\Bigl(\frac{2πnt}{T}\Bigr)\enspace dt\tag{94}$$
$$a_0=\frac{2}{T}\int_{-\frac{1}{2}T}^{\frac{1}{2}T}\enspace f(t)\enspace dt\tag{95}$$
式(92)の回帰関数は、大きさ \(\frac{1}{2}a_0\) の非周期成分と、振動数 \(1/T\) の整数 \(n\) 倍の振動数をもつ調和関数の無限級数によって表されます。
さて、\(sin\) 関数および \(cos\) 関数は、つぎのように書き換えることができ、
$$cos(nωt)=\frac{1}{2}(e^{inωt}+e^{-inωt})$$
$$sin(nωt)=\frac{1}{2i}(e^{inωt}-e^{-inωt})$$
式(92)に代入すると、
$$f(t)=\sum_{n=-∞}^∞\enspace c_n\enspace exp(-inωt)\tag{96}$$
ここで、 \(ω\) は各振動数 \(ω=2π/T\) であり、
$$c_0=\frac{1}{2}a_0,\enspace c_{-n}=\frac{1}{2}(a_n-ib_n),\enspace c_n=\frac{1}{2}(a_n+ib_n)$$
この指数関数の無限級数に対して直行性を利用して、係数 \(c_n\) は次のように直接計算することができます。
$$c_n=\frac{1}{T}\int_{-\frac{1}{2}T}^{\frac{1}{2}T}\enspace f(t)\enspace exp\Bigl(\frac{2πint}{T}\Bigr)\enspace dt$$
フーリエ級数は、変数の限られた範囲 \((0≦t≦T)\) における非周期関数にも使用でき、最も長い周期が \(T\) である調和波の和として表されます。もちろん、この非周期関数を近似したフーリエ級数においても、周期Tごとに非周期関数が繰り返される周期関数を形成します。ただし、範囲 \(0≦t≦T\) のみを考えているため、このことは問題ではありません。また範囲 \(0≦t≦T\) が長いほど、フーリエ級数の基本振動数は低くなります。
下図はフーリエ級数の係数を角振動数に対してペアーのスペクトルとしてプロットした線スペクトルです。範囲 \(0≦t≦T\) の非周期関数の表現における逐次項の角振動数は、\(ω_1=2π/T,ω_2=2ω_1,・・・・,ω_n=nω_1\) です。
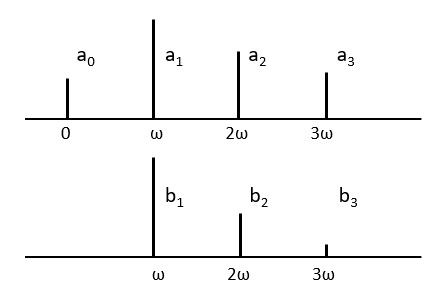
したがって、近似範囲が広がると、線スペクトルの間隔がより密になります。近似精度は、含まれる最高振動数成分によって異なります。これは、持続時間 \(T_1\) の局所的な変動は、\(T_1\) より長い周期( \(2π/T_1\) 未満の振動数)の項では表すことができないためです。したがって、急激な変動などの詳細な再現が必要になるにつれて、必要なフーリエ項の数も増加します。
フーリエ積分
関数が反復的ではなく、変数の全範囲にわたって表現する必要がある場合、たとえば関数が孤立したパルスで構成されている場合などにはフーリエ積分で表現できます。関数 \(f(t)\) の積分表示は、
$$f(t)=\frac{1}{2π}\int_{-∞}^∞\enspace e^{-iωt}\enspace f^*(ω)dω\tag{97}$$
ここに、
$$f^*(ω)=\int_{-∞}^∞\enspace e^{iωt}\enspace f(t)dt\tag{98}$$
関数 \(f(ω)\) は一般に \(f(t)\) のフーリエ変換、式(97)は逆変換を定義しています。式(97) と 式(98) の積分を実施する簡略化した方法は、定義の間隔が無制限に拡大するフーリエ級数の極限ケースを考慮することです。実際、フーリエ級数の周波数スペクトルの構造は、周波数空間内で項を密に詰め込むことによって関数の表現範囲を無限に増やすことが出来ることを示唆しています。範囲が限界を超えて増加する限界では、離散スペクトルは実際には \(f(ω)\) で表される連続スペクトルに変換されるはずです。この論点において、\(f(ω)dω\) は \(ω\) における振幅の微少周波数帯域 \(dω\) における寄与を表わします。
さて、\(-1/2T<t<1/2T\) における関数 \(f(t)\) を考えてみましょう。 \(f(t)\) は複素フーリエ級数によって、つぎのように表わされます。
$$f(t)=\sum_{-∞}^∞\Bigl[\frac{1}{T}\int_{-\frac{1}{2}T}^{\frac{1}{2}T}\enspace f(s)\enspace exp\Bigl(\frac{2πins}{T}\Bigr)ds\Bigr]\enspace exp\Bigl(-\frac{2πint}{T}\Bigr)\tag{99}$$
\(ω_n=2πn/T\) と定義すると \(ω_{n+1}-ω_n=2π/T\) であり、T の値が大きい場合、小さな周波数範囲 \(dω\) は \(ω/(2π/T)\) 項を包含すると言えます。これらの式(99)の合計に対する寄与は次のようになります。
$$\frac{TΔω}{2π}\Bigl[\frac{1}{T}\int_{-\frac{1}{2}T}^{\frac{1}{2}T}\enspace f(s)\enspace e^{iω_ns}ds\Bigr]\enspace e^{-iω_nt}$$
形式的に極限 \(T→∞\) とすると、式(99)の合計は積分になり、次の結果が得られます。
$$f(t)=\frac{1}{2π}\int_{-∞}^{∞}e^{-iωt}dω\int_{-∞}^{∞}f(s)e^{iωs}ds\tag{100}$$
式(100)はフーリエ積分と呼ばれ、式(98)によってフーリエ変換、式(97)によってフーリエ逆変換されることを示しています。
以上、参考になれば幸いです。



コメント