 波動と相互作用問題
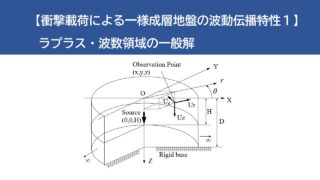
波動と相互作用問題【衝撃載荷による一様成層地盤の波動伝播特性1】ラプラス・波数領域の一般解
今回のシリーズでは、剛基盤上の一様成層地盤の波動伝播特性について、勉強していきます。まずは、ラプラス・波数領域の一般解を導きます。その際、周方向にフーリエ級数展開し、半径方向にはハンケル変換を行います。 フーリエ・ベッセ...
 波動と相互作用問題
波動と相互作用問題 波動と相互作用問題
波動と相互作用問題 波動と相互作用問題
波動と相互作用問題 波動と相互作用問題
波動と相互作用問題 波動と相互作用問題
波動と相互作用問題 波動と相互作用問題
波動と相互作用問題 波動と相互作用問題
波動と相互作用問題 波動と相互作用問題
波動と相互作用問題 波動と相互作用問題
波動と相互作用問題 波動と相互作用問題
波動と相互作用問題