基礎反力の算定(1)で求めた一般解に、円形基礎に関するパラメータを代入して、円形基礎の反力式を導きます。台形分布となる場合は陽に反力が得られますが、三角形分布となる場合には反力が分布する範囲を角度\(α\)とおき、三角関数に関する積分を実施して解を求めます。
円形基礎の反力式の導出
基礎全面に反力が発生している場合
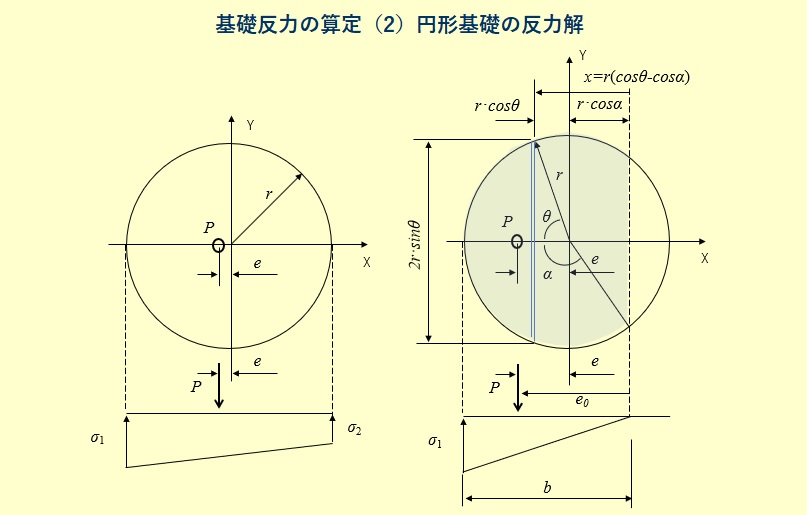
下図のように基礎断面、記号、台形反力分布を定義します。
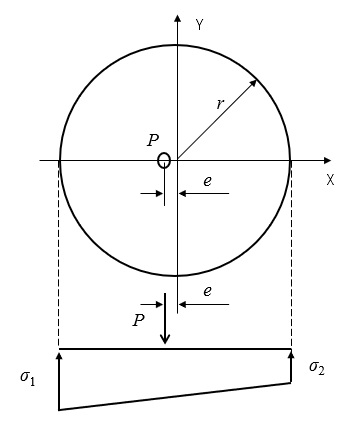
円形基礎の場合、基礎端部から重心までの距離\(g\)、面積\(A\)、断面二次モーメント\(I_G\)、基礎幅\(B\)は、
$$g=r\quad ,\quad A=πr^2\quad ,\quad I_G=\frac{π}{4}r^4\quad ,\quad B=2r$$
これらを基礎反力の算定(1)一般解と矩形断面で求めた一般解に代入すれば、
$$σ_1=\frac{P}{A}+\frac{Pe}{I_G}(B-g)=\frac{P}{A}(1+\frac{4e}{r})\tag{19}$$
$$σ_2=\frac{P}{A}-\frac{Pe}{I_G}g=\frac{P}{A}(1-\frac{4e}{r})\tag{20}$$
台形分布から三角形分布に変わるときの重心から荷重作用点までの距離\(e’\)は、
$$e’=\frac{I_G}{Ag}=\frac{r}{4}\tag{21}$$
\(e=e’\)のときの\(σ_1\)は、
$$σ_1=\frac{2P}{A}\tag{22}$$
基礎の一部に反力が発生している場合
下図のように基礎断面、記号、三角形反力分布を定義します。
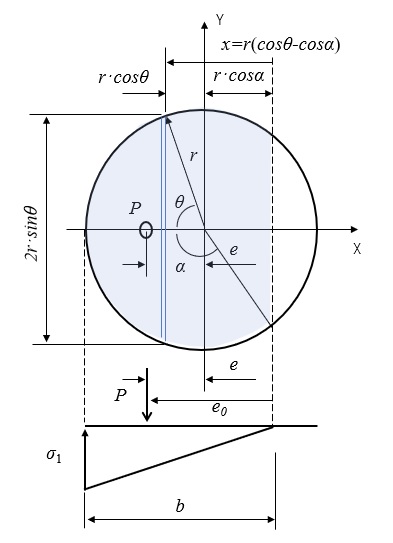
基礎反力が0となるx位置(\(θ=α\))に関する断面一次モーメント\(G_n\)と断面二次モーメント\(I_n\)を求めて、これらを一般解に代入して\(b\)および\(σ_1\)を求めます。まず、上図の定義から、
$$x=r(cosθ-cosα)$$
であるので、
$$\frac{dx}{dθ}=rsinθ$$
基礎反力が0となるx位置に関する断面一次モーメント\(G_n\)は、
$$G_n=\int_0^α x(2rsinθ)dx=\int_0^α r(cosθ-cosα)(2rsinθ)(rsinθ)dθ$$
上式を整理して積分すると、
$$G_n=2r^3\int_0^α (cosθ-(cosθ)^3-(sinθ)^2cosα)dθ$$
$$=2r^3\biggl[sinθ+\frac{1}{3}(sinθ)^3-sinθ-\biggl(\frac{θ}{2}-\frac{sin2θ}{4}\biggr)cosα)\biggr]_0^α$$
$$=r^3\bigl\{\frac{sinα}{3}\big(2+(cosα)^2\big)-αcosα\bigr\}$$
基礎反力が0となるx位置に関する断面二次モーメント\(I_n\)は、
$$I_n=\int_0^α x^2(2rsinθ)dx\int_0^α r^2(cosθ-cosα)^2(2rsinθ)(rsinθ)dθ$$
上式を整理して積分すると、
$$I_n=2r^4\int_0^α (-(cosθ)^4+2(cosθ)^3cosα+(cosθ)^2(1-(cosα)^2)$$
$$-2cosθ・cosα+(coaα)^2)dθ$$
$$=2r^4\biggl[-\frac{3θ}{8}-\frac{sin2θ}{4}-\frac{sin4θ}{32}+2\biggl(-\frac{(sinθ)^3}{3}+sinθ\biggr)cosα$$
$$+\biggl(\frac{θ}{2}+\frac{sin2θ}{4}\biggr)(1-(cosα)^2)-2sinθ・cosα+θ(cosα)^2)\biggr]_0^α$$
$$=r^4\bigl\{α\big(\frac{1}{4}+(cosα)^2\big)-sinα・cosα\big(\frac{13}{12}+\frac{(cosα)^2}{6}\big)\bigr\}$$
つぎに、基礎反力の算定(1)の式(14)において、上図の関係から\(f-b=rcosα\)であるので、
$$e=\frac{I_n}{G_n}+(f-b)\frac{I_n}{G_n}+rcosα$$
上式に\(G_n\)と\(I_n\)を代入して整理すると、
$$e=\frac{\displaystyle r^4\bigl\{α\big(\frac{1}{4}+(cosα)^2\big)-sinα・cosα\big(\frac{13}{12}+\frac{(cosα)^2}{6}\big)\bigr\}}{\displaystyle r^3\bigl\{\frac{sinα}{3}\big(2+(cosα)^2\big)-α・cosα\bigr\}}+rcosα$$
よって、
$$\frac{e}{r}=\frac{\displaystyle \frac{α}{4}-sinα・cosα\big(\frac{5}{12}-\frac{(cosα)^2}{6}\big)}{\displaystyle \frac{sinα}{3}\big(2+(cosα)^2\big)-α・cosα}\tag{23}$$
式(23)より繰り返し計算より\(α\)を求め、基礎反力の算定(1)の式(13)に代入して\(σ_1\)を求める。
$$σ_1=\frac{P・b}{G_n}=\frac{P(1-cosα)}{\displaystyle r^2\bigl\{\frac{1}{3}sinα\big(2+(cosα)^2\big)-α・cosα\bigr\}}\tag{24}$$
ここで、面積\(A=πr^2\)として、
$$σ_1=C\frac{P}{A}\tag{25}$$
とおくと、\(C\)はつぎのように表される。
$$C=\frac{3π(1-cosα)}{sinα\big(2+(cosα)^2\big)-3α・cosα}\tag{26}$$
円形基礎の反力の解のまとめ
導出された数式を式番号を改めて設定してまとめると、以下のようになります。
\(e<e’=\frac{r}{4}\)のとき台形分布となり、次式より反力を計算できる。
$$σ_1=\frac{P}{A}(1+\frac{4e}{r})\tag{27}$$
$$σ_2=\frac{P}{A}(1-\frac{4e}{r})\tag{28}$$
\(e>e’=\frac{r}{4}\)のとき三角形分布となり、下式より反力が分布する範囲の角度\(α\)を求めることで反力および反力分布幅\(b\)を計算できる。
$$\frac{e}{r}=\frac{\displaystyle \frac{α}{4}-sinα・cosα\big(\frac{5}{12}-\frac{(cosα)^2}{6}\big)}{\displaystyle \frac{sinα}{3}\big(2+(cosα)^2\big)-α・cosα}\tag{29}$$
$$σ_1=\frac{P(1-cosα)}{\displaystyle r^2\bigl\{\frac{1}{3}sinα\big(2+(cosα)^2\big)-α・cosα\bigr\}}\tag{30}$$
$$b=r(1-cosα)\tag{31}$$
\(e=e’=\frac{r}{4}\)のときは以下のようになる。
$$σ_1=\frac{2P}{A}\tag{32}$$
$$b=2r\tag{33}$$
なお、上式を用いて円形基礎の反力解を基礎反力の計算(3)円形基礎反力の算定:Newtonの逐次近似法とゴールシークにおいて求めていますので、ご興味のある方はご覧ください。




コメント