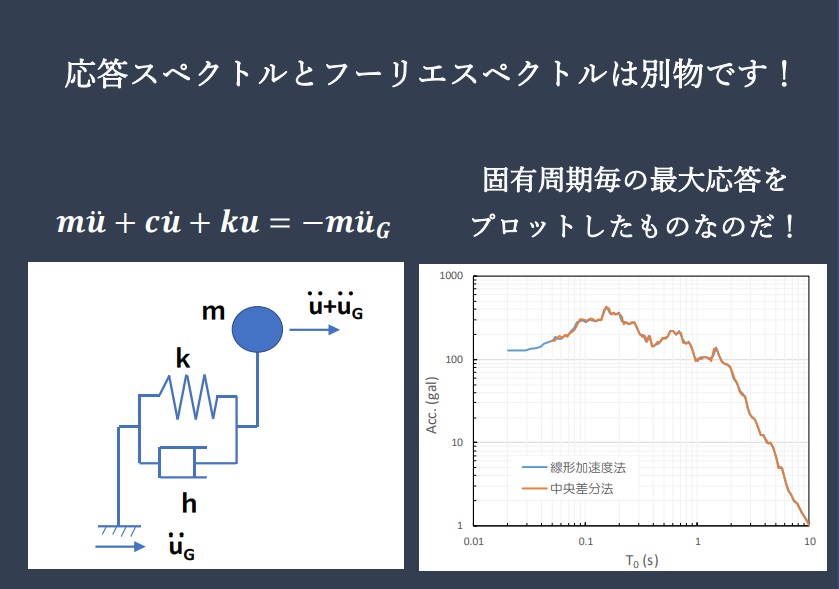
地震応答スペクトルは構造物の設計でよく用いられますが、地震波のフーリエスペクトルと混同されている方が多くいます。地震応答スペクトルは構造物の最大応答を構造物の固有周期ごとに示したものなのに対して、地震波のフーリエスペクトルは地震波の周期(振動数)ごとの振幅を示したものです。ExcelVBAを用いた地震応答スペクトルの計算を行っていきますが、今回はその基礎式(微分方程式)までを紹介します。
1自由度系の運動方程式
いま、1自由度系(1つの質点上に、水平方向の1自由度のみとします)の質量 \(m\) とバネ剛性 \(k\)、減衰定数 \(c\) をもつ構造物を仮定します。この固定端(構造物の基礎に当たります)に地震波加速度 \(\ddot{u}_G\) が入力されて構造物が揺らされると、質点には絶対加速度 \(\ddot{u}+\ddot{u}_G\) が発生し、慣性力が働きます。それに応じて質点には速度と変位が発生していますが、固定端との相対速度 \(\dot{u}\) によってダッシュポットを介した減衰力、相対変位 \(u\) により剛性を介した力が、それぞれ質点に働きます。
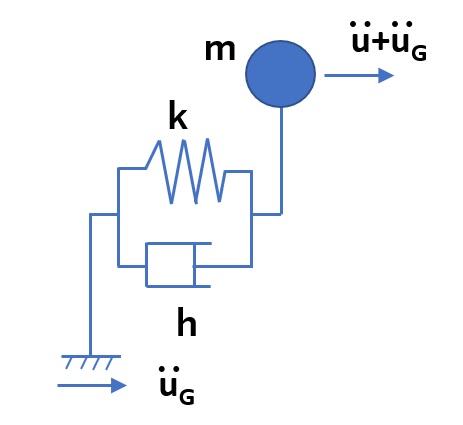
この質点に働く力の釣り合いから、1自由度系の運動方程式はつぎのように表されます。
$$m(\ddot{u}+\ddot{u}_G)+c\dot{u}+ku=0\tag{1}$$
両辺を \(m\) で割ると、
$$\ddot{u}+\frac{c}{m}\dot{u}+\frac{k}{m}u=-\ddot{u}_G\tag{2}$$
ここで、
$$\frac{k}{m}=ω_0^2\tag{3}$$
\(ω_0\) は固有角振動数であり、\(\displaystyleω_0=\frac{2π}{T_0}\)、\(T_0\) は構造物の固有周期です。1自由度系であるため、固有周期は1次周期のみになります。
また、減衰比 \(h\) をつかって \(\displaystyle\frac{c}{m}=2hω_0\) とおきます。 (\(h\) は減衰定数、減衰係数などと呼ばれることも多く、\(c\) と紛らわしい場合が多いように思いますが、入力値としては \(h\) の数値を表していることが多いようです。)
以上より、1自由度系の運動方程式は、
$$\ddot{u}+2hω_0\dot{u}+ω_0^2u=-\ddot{u}_G\tag{3}$$
となり、この微分方程式を解くことで、既知の地震加速度 \(\ddot{u}_G\) が作用した場合の構造物の応答値を得ることができます。
地震応答スペクトルとは
上述した1自由度系の運動方程式は、構造物の固有周期 \(T_0\) に対して定式化した運動方程式です。これを用いれば、様々な固有周期をもつ構造物に対して、ある地震波が入力された場合の構造物の応答を求めることができます。地震応答スペクトルは、様々な固有周期をもつ構造物に対して、ある地震波が入力された場合の最大応答値をプロットしたものです。つまり、構造物の固有周期が分かれば、地震応答スペクトル図を利用して、ある特定の地震波に対して構造物に作用する加速度、速度、変位が求められます。
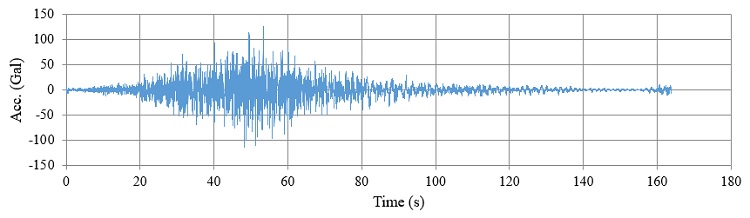
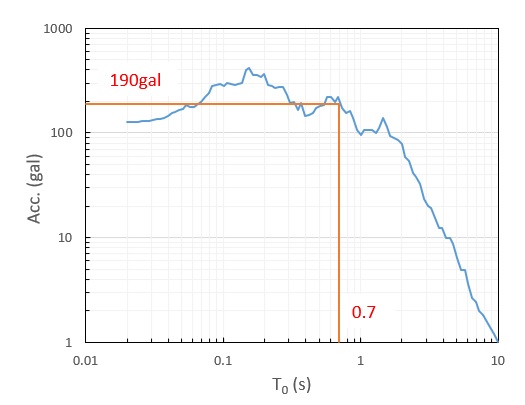
いま、下図のような地震加速度に対して、減衰比 \(h=0.05\) として求めた加速度応答スペクトルを示します。(横軸は構造物の固有周期としましたが、固有振動数としてプロットする場合もあります。)
たとえば、構造物の固有周期が \(T_0 =0.7s\) のとき、この地震波が入力された場合の構造物の加速度は、190galとなることがわかります。
フーリエスペクトルとの違い
フーリエスペクトルは、地震波をフーリエ変換したものをプロットしたものです(フーリエ変換の計算については、ExcelVBAで高速フーリエ変換FFTを作成してみたや高速フーリエ変換アルゴリズムの疑問 ポイントを簡単に解説なども参考になります)。振幅に \(T/2\) (\(T\) はフーリエ変換時の基本周期)を乗じたものをフーリエ振幅スペクトルと呼び、一般にフーリエスペクトルと言うと振幅スペクトルを指します。同様に位相をプロットしたものを位相スペクトル、振幅の2乗をプロットしたものをパワースペクトルあるいはエネルギースペクトルと呼ばれます。
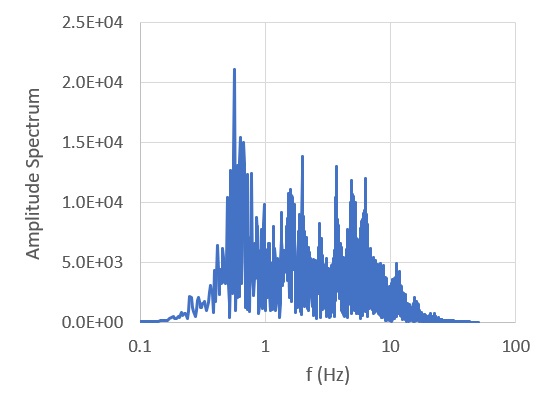
先ほどの地震波のフーリエ振幅スペクトルを振動数に対してプロットしたものを下図に示します。フーリエ振幅スペクトルは、地震波自体の振動数成分の大きさを示したもので、地震波の特性を示したものです。構造物の応答値を示した応答スペクトルとは、全く異なるものであることが分かります。
次回からはVBAで応答スペクトルを計算してみます。






コメント