基礎反力の算定(1)で求めた一般解に、正方形基礎に関するパラメータを代入して、正方形基礎の反力式を導きます。このときの正方形基礎は対角線上に反力が発生する形状(ひし形)とします。台形分布となる場合と基礎幅の半分以下の範囲に三角形分布となる場合はrとeから直接反力が得られますが、基礎幅の半分以上の範囲に三角形分布となる場合には反力が分布する範囲を変数におき、Newtonの逐次近似法を用いて求めます。なお、ここに示した反力解は文献等でのチェックを行っていませんので、反力解のご利用に際しては反力解の定式化のチェックをお願いします。
正方形基礎の反力式の導出
対角線上に反力が発生する(荷重が対角線上を動く)場合には、基礎全面に反力が発生する(台形分布する)場合と基礎の一部に反力が発生する(三角形分布)場合があります。さらに基礎の一部に反力が発生する場合には、分布幅が0~r(反力分布範囲が三角形)の場合とr~2r(反力分布範囲が三角形と台形の和になる)の場合に分けて反力解を計算していきます。
基礎全面に反力が発生している場合
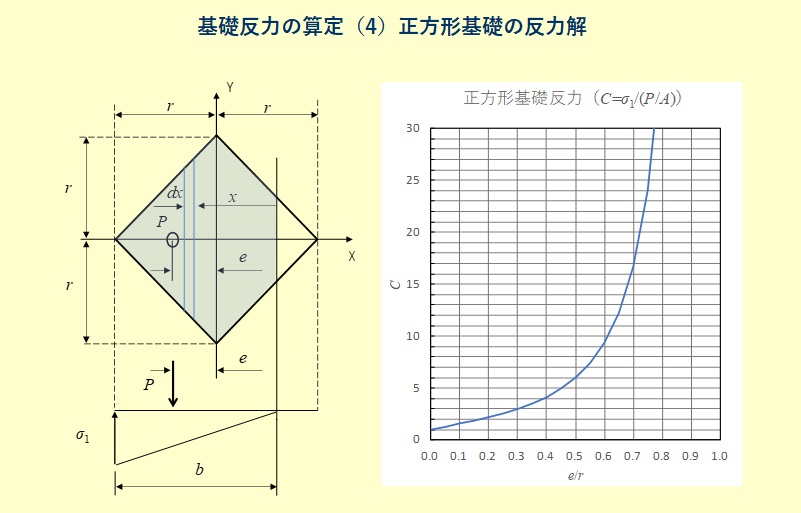
下図のように基礎断面、記号、台形反力分布を定義します。正方形の方向は、対角線を反力の分布方向に合わせます。
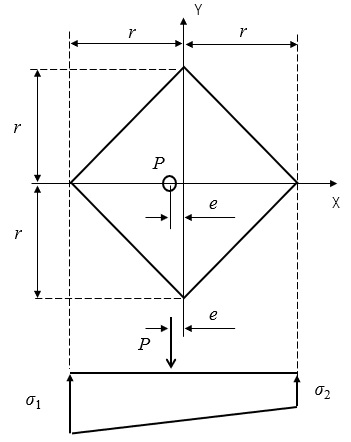
正方形基礎の場合、基礎端部から重心までの距離\(g\)、面積\(A\)、断面二次モーメント\(I_G\)、基礎幅\(B\)は、
$$g=r\quad ,\quad A=2r^2\quad ,\quad I_G=\frac{r^4}{3}\quad ,\quad B=2r$$
これらを基礎反力の算定(1)一般解と矩形断面で求めた一般解に代入すれば、
$$σ_1=\frac{P}{A}+\frac{Pe}{I_G}(B-g)=\frac{P}{A}(1+\frac{6e}{r})\tag{42}$$
$$σ_2=\frac{P}{A}-\frac{Pe}{I_G}g=\frac{P}{A}(1-\frac{6e}{r})\tag{43}$$
台形分布から三角形分布に変わるときの重心から荷重作用点までの距離\(e’\)は、
$$e’=\frac{I_G}{Ag}=\frac{r}{6}\tag{44}$$
\(e=e’\)のときの\(σ_1\)は、
$$σ_1=\frac{2P}{A}\tag{45}$$
基礎反力範囲がr<=d<2rの場合
下図のように基礎断面、記号、三角形反力分布を定義します。
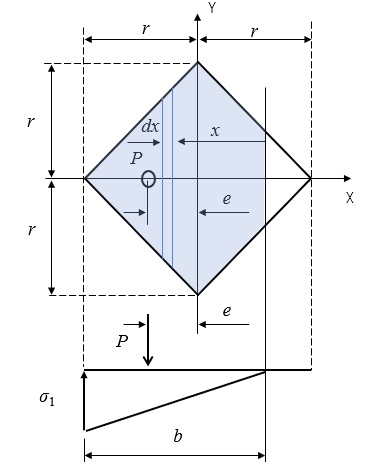
基礎反力が0となるx位置(反力分布幅\(b\)の端部)に関する断面一次モーメント\(G_n\)と断面二次モーメント\(I_n\)を求めて、これらを一般解に代入して\(b\)および\(σ_1\)を求めます。まず、基礎反力が0となるx位置に関する断面一次モーメント\(G_n\)は、
$$G_n=\int_0^{b-r} x\{2r-2(b-r-x)\}dx+\int_{b-r}^b x\{2r-2(x-b+r)\}dx$$
上式を整理して積分すると、
$$G_n=\int_0^{b-r} \{x・(4r-2b)+2x^2\}dx+\int_{b-r}^b (-2x^2+2bx)dx$$
$$=\biggl[-\frac{2x^3}{3}+bx^2\biggr]_0^{b-r}+\biggl[x^2・(2r-b)+\frac{2x^3}{3}\biggr]_{b-r}^b$$
$$=\frac{1}{3}\bigl\{b^3-2(b-r)^3\bigr\}$$
基礎反力が0となるx位置に関する断面二次モーメント\(I_n\)は、
$$I_n=\int_0^{b-r} x^2\{2r-2(b-r-x)\}dx+\int_{b-r}^b x^2\{2r-2(x-b+r)\}dx$$
上式を整理して積分すると、
$$I_n=\int_0^{b-r} \{x^2・(4r-2b)+2x^3\}dx+\int_{b-r}^b (-2x^3+2bx^2)dx$$
$$=\biggl[\frac{2x^3}{3}(2r-b)+\frac{x^4}{2}\biggr]_0^{b-r}+\biggl[-\frac{x^4}{2}+\frac{2bx^3}{3}\biggr]_{b-r}^b$$
$$=\frac{1}{6}\bigl\{b^4-2(b-r)^4\bigr\}$$
つぎに、基礎反力の算定(1)の式(14)において、上図の関係から\(f=r\)であるので、
$$e=\frac{I_n}{G_n}+(r-b)$$
上式に\(G_n\)と\(I_n\)を代入して整理すると、
$$e=\frac{\displaystyle b^4-2(b-r)^4}{\displaystyle 2\bigl\{b^3-2(b-r)^3\bigr\}} +r-b$$
$$=\frac{\displaystyle rb^3-\frac{b^4}{2}+(b-r)^4}{\displaystyle b^3-2(b-r)^3}$$
ここで、\(b=kr\quad ,\quad 1<k\text{≦}2\)とおくと、
$$\frac{e}{r}=\frac{\displaystyle k^3-\frac{k^4}{2}+(k-1)^4}{\displaystyle \bigl\{k^3-2(k-1)^3\bigr\}}\tag{46}$$
式(46)より繰り返し計算より\(k\)を求め、基礎反力の算定(1)の式(13)に代入して\(σ_1\)を求める。
$$σ_1=\frac{P・b}{G_n}=\frac{3Pb}{\displaystyle b^3-2(b-r)^3}\tag{47}$$
ここで、面積\(A=2r^2\)であるので、
$$σ_1=C\frac{P}{A}\tag{48}$$
とおくと、\(C\)はつぎのように表される。
$$C=\frac{6r^2b}{b^3-2(b-r)^3}\tag{49}$$
基礎反力範囲がd<rより狭い場合
基礎反力の分布範囲が\(d<r\)の場合には、基礎反力が0となるx位置(反力分布幅\(b\)の端部)に関する断面一次モーメント\(G_n\)と断面二次モーメント\(I_n\)の積分範囲が三角形範囲のみとなります。
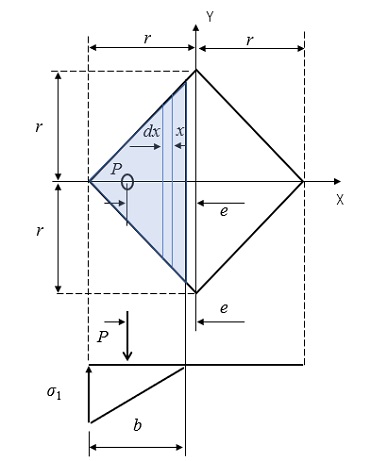
基礎反力が0となるx位置に関する断面一次モーメント\(G_n\)は、
$$G_n=\int_0^{b} x\{2r-2(r-b+x)\}dx=\int_0^{b} 2・(bx-x^2)dx$$
$$=\biggl[bx^2-\frac{2x^3}{3}\biggr]_0^{b}$$
$$=\frac{b^3}{3}$$
基礎反力が0となるx位置に関する断面二次モーメント\(I_n\)は、
$$I_n=\int_0^{b} x^2\{2r-2(r-b+x)\}dx=\int_{0}^b (2bx^2-2x^3)dx$$
$$=\biggl[\frac{2bx^3}{3}-\frac{x^4}{2}\biggr]_{0}^b$$
$$=\frac{b^4}{6}$$
つぎに、基礎反力の算定(1)の式(14)において、上図の関係から\(f=r\)であるので、
$$e=\frac{I_n}{G_n}+(r-b)$$
上式に\(G_n\)と\(I_n\)を代入して整理すると、
$$e=\frac{\displaystyle \bigg(\frac{b^4}{6}\bigg)}{\displaystyle \bigg(\frac{b^3}{3}\bigg)} +r-b=r-\frac{b}{2}$$
よって、
$$b=2・(r-e)\tag{50}$$
基礎反力の算定(1)の式(13)より\(σ_1\)を求める。
$$σ_1=\frac{P・b}{G_n}=\frac{3P}{b^2}$$
ここで、面積\(A=2r^2\)であるので、
$$σ_1=\frac{P}{A}\frac{6r^2}{b^2}\tag{51}$$
$$σ_1=C\frac{P}{A}$$
とおくと、\(C\)はつぎのように表される。
$$C=\frac{6r^2}{b^2}\tag{52}$$
Newtonの逐次近似法の適用
式(46)より、両辺の差をとって、
$$Z(k)=\frac{\displaystyle k^3-\frac{k^4}{2}+(k-1)^4}{\displaystyle \bigl\{k^3-2(k-1)^3\bigr\}}-\frac{e}{r}\tag{53}$$
と定義すれば、基礎反力が分布する幅\(b\)は上式の\(Z(k)\)がゼロになるときの\(k\)の値から\(b=kr\)として求まります。
さて、\(Z(k)\)がゼロとなる\(k\)を求めるために、Newtonの逐次近似法を用います。Newtonの逐次近似法は、\(k_1\)における勾配\(Z'(k_1)\)を求めて、この勾配の直線を\(Z(k_1)\)の点から引いてX軸と交わる点(\(Z(k)=0\))のX座標を\(k_2\)とすると、
$$Z’(k_1)=\frac{Z(k_1)}{k_2- k_1}$$
$$∴k_2=k_1-\frac{Z(k_1)}{Z’(k_1)}$$
よって、上式に\(k_1\)の値を入力して得られた\(k_2\)を\(k_1\)と置き直して計算します。これを繰り返し、次式で定義される誤差をε以下になるまで実施します。
$$|1-\frac{k_1}{k_2}|<ε$$
得られた解\(k_2\)を式(47)に代入することで、反力\(σ_1\)が求まります。なお、\(1<k≦2\)であり、実際の計算では初期値として\(k=1\)としています。
さて、\(Z(k)\)と\(Z’(k)\)の計算は、
$$f(k)=k^3-\frac{k^4}{2}+(k-1)^4=\frac{k^4}{2}-3k^3+6k^2-4k+1$$
$$h(k)=\{k^3-2(k-1)^3\}=-k^3+6k^2-6k+2$$
とおくと、
$$Z(k)=\frac{f(k)}{g(k)}-\frac{e}{r}$$
同式を\(k\)で1回微分すると、
$$Z’ (x)=\frac{f'(x)g(x)-f(x)g'(x)}{g(x)^2}$$
$$f'(k)=2k^3-9k^2+12k-4$$
$$h'(k)=-3k^2+12k-6$$
であり、これらより計算できます。
以上より計算した\(e/r\)と\(C\)の関係をグラフとして示します。
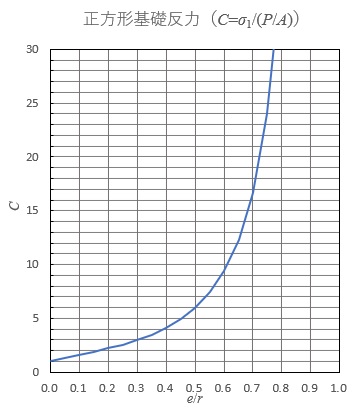
参考:正方形基礎反力算定のプロシージャ
参考に実際の計算に用いたExcelシートとNewtonの逐次近似法のプロシージャを示します。Excelシート上には、青色セル内に入力値を入力して計算実行ボタンを押すと、反力分布の判定と出力される出力されるように作成しました。計算実行ボタン(コマンドボタン)の設定は、VBAでコマンドボタンから鋼管杭の断面諸元計算のプロシージャを実行する!に簡単に説明していますので、必要であればご覧ください。
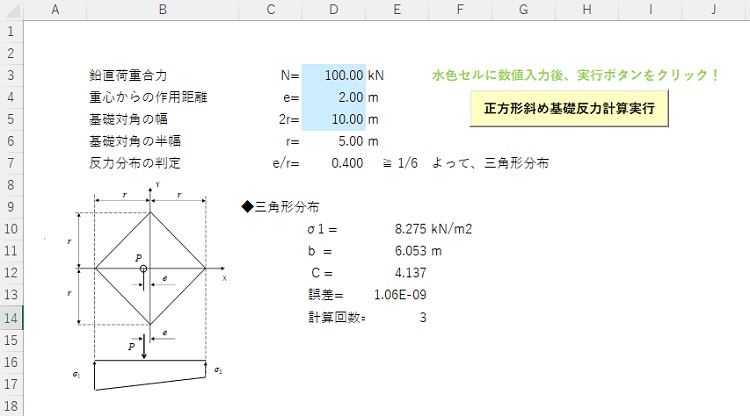
以下に今回の計算に用いたプロシージャのコピーを示します。

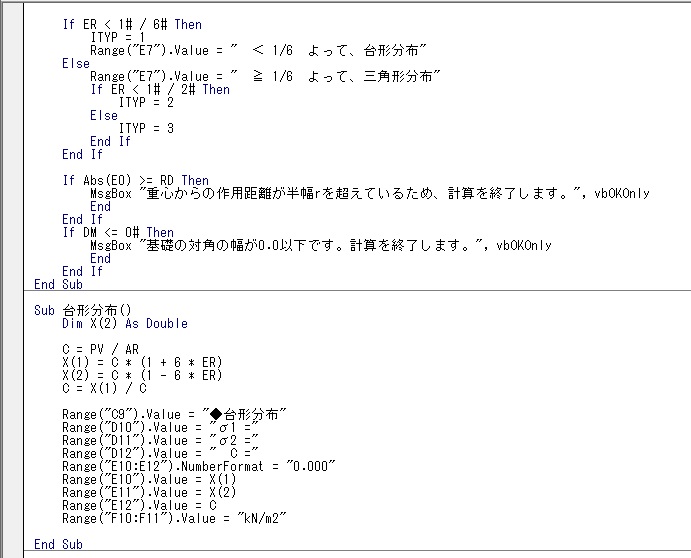
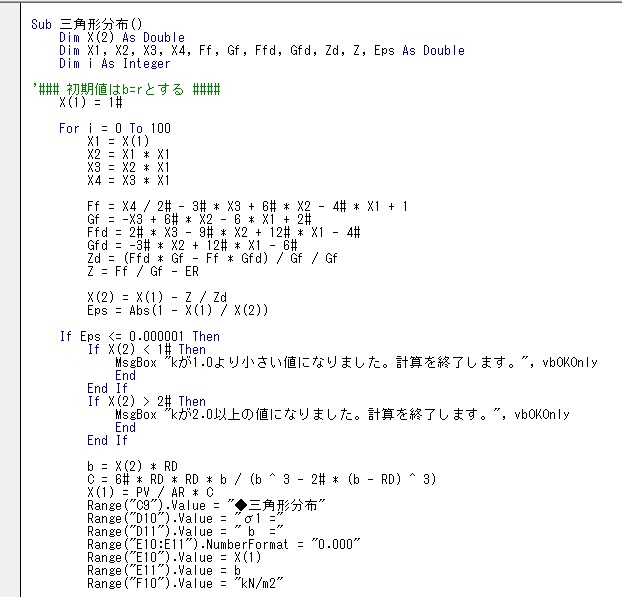
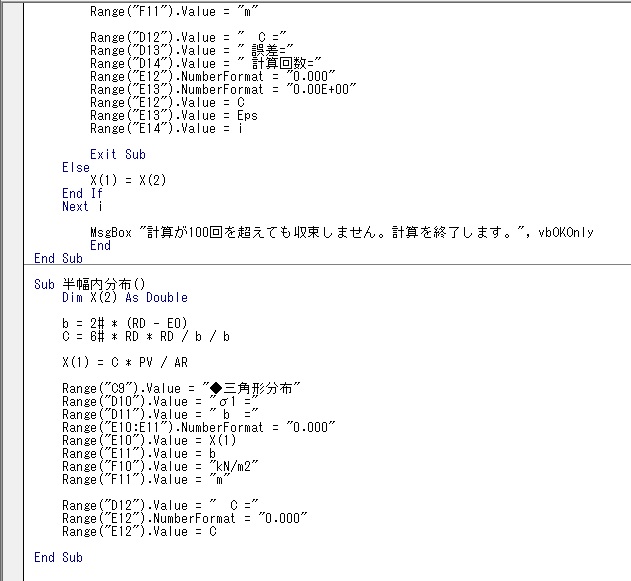
正方形基礎の反力解のまとめ
導出された数式を式番号を改めて設定してまとめると、以下のようになります。
\(e<e’=\frac{r}{6}\)のとき台形分布となり、次式より反力を計算できる。
$$σ_1=\frac{P}{A}(1+\frac{6e}{r})\tag{53}$$
$$σ_2=\frac{P}{A}(1-\frac{6e}{r})\tag{54}$$
\(\frac{r}{6} \leq e\) \(<\frac{r}{4}\)のとき三角形分布となり、下式が成り立つ\(k\)を求めることで反力および反力分布幅\(b\)を計算できる。
$$\frac{e}{r}=\frac{\displaystyle k^3-\frac{k^4}{2}+(k-1)^4}{\displaystyle \bigl\{k^3-2(k-1)^3\bigr\}}\tag{55}$$
$$σ_1=\frac{P}{A}\frac{6r^2b}{b^3-2(b-r)^3}\tag{56}$$
$$b=kr\tag{57}$$
\(\frac{r}{4}\leq e\)のとき三角形分布となり、以下のようになる。
$$σ_1=\frac{P}{A}\frac{6r^2}{b^2}\tag{58}$$
$$b=2・(r-e)\tag{59}$$




コメント