地震応答スペクトル計算(1)に示した1自由度系の運動方程式を線形加速度法で時刻歴解析を行い、地震応答スペクトルを求めてみます。ExcelはOffice2021を用いました。中央差分法についても説明していますのでご興味のある方は、ExcelVBAで地震応答スペクトル計算(2)中央差分法で運動方程式を解くをご覧ください。
線形加速度法の定式化
ExcelVBAで地震応答スペクトル計算(2)に示した1自由度系の運動方程式は、時間\(t=(n+1)Δt\) においてつぎのように表せます。
$$\ddot{u}_{n+1}+2hω_0・\dot{u}_{n+1}+ω_0^2・u_{n+1}=-\ddot{u}_{Gn+1}\tag{1}$$
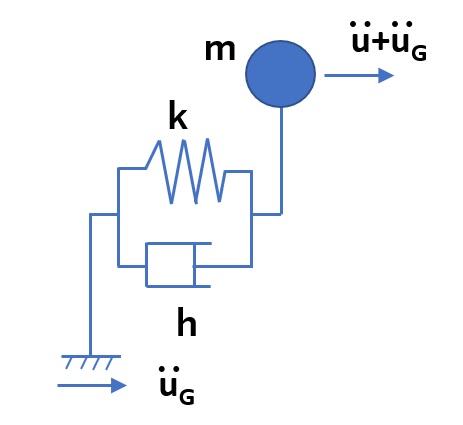
ここで、\(ω_0\) は構造物の固有角振動数、\(h\) は減衰比です。
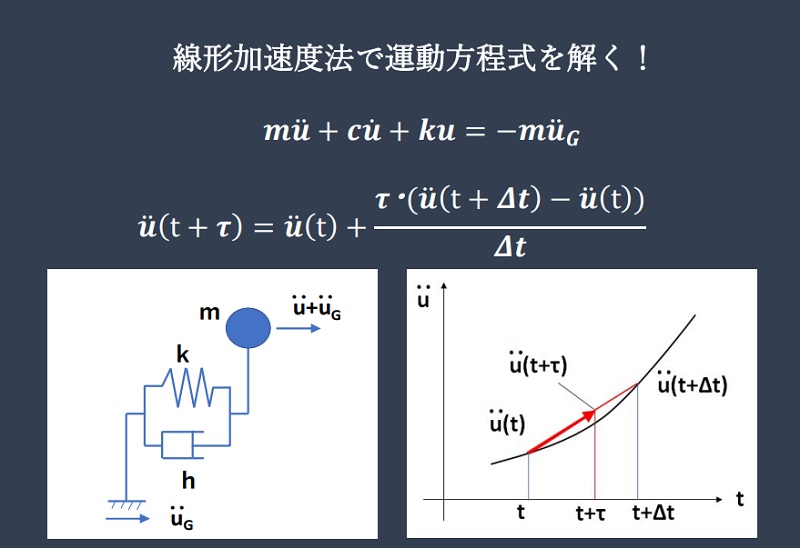
さて、線形加速度法では加速度の変化率を線形と仮定します。下図に示すように、加速度の時間 \(t\) から \(Δt\) までの変化を線形と仮定すると、\(t+τ\) での加速度は、
$$\ddot{u}(t+τ)=\ddot{u}(t)+\frac{τ ・(\ddot{u}(t+Δt)-\ddot{u}(t))}{Δt}\tag{2}$$
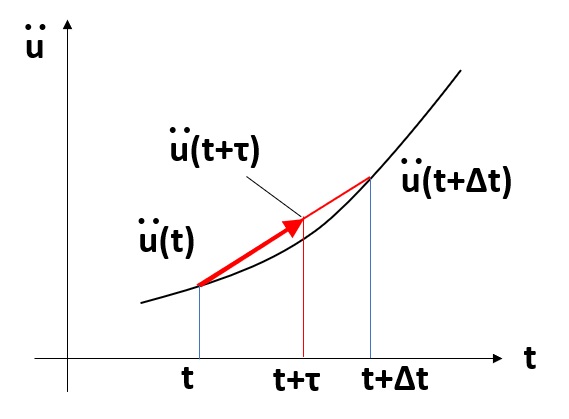
式(2)を \(τ\) に関して積分すると相対速度がつぎのように得られます。
$$\dot{u}(t+τ)=τ ・\ddot{u}(t)+\frac{τ^2 ・(\ddot{u}(t+Δt)-\ddot{u}(t))}{2Δt}+C_1\tag{3}$$
さらに積分して変位を求めると、
$$u(t+τ)=\frac{τ^2 ・\ddot{u}(t)}{2}+\frac{τ^3 ・(\ddot{u}(t+Δt)-\ddot{u}(t))}{6Δt}+τ ・C_1+C_2\tag{4}$$
\(τ=0\) のとき、式(3)より \(C_1=\dot{u}(t)\) 、式(4)より \(C_2=u(t)\) となります。
(実は式(4)は \(τ=Δt\) としたとき、\(t+Δt\) で展開したテイラー展開の3次項までに一致することになります。)
ここで、\(τ=Δt\) とすると、式(3)と式(4)より、
$$\dot{u}(t+Δt)=\dot{u}(t)+\frac{Δt ・(\ddot{u}(t+Δt)+\ddot{u}(t))}{2}\tag{5}$$
$$u(t+Δt)=u(t)+Δt\dot{u}(t)+\frac{(Δt)^2 ・\ddot{u}(t)}{3}+\frac{(Δt)^2 ・\ddot{u}(t+Δt)}{6}\tag{6}$$
\(t=nΔt\) として式(1)と同じ表記に直すと、
$$\dot{u}_{n+1}=\dot{u}_{n}+\frac{Δt ・(\ddot{u}_{n+1}+\ddot{u}_n)}{2}\tag{7}$$
$$u_{n+1}=u_n+Δt\dot{u}_n+\frac{(Δt)^2 ・\ddot{u}_n}{3}+\frac{(Δt)^2 \ddot{u}_{n+1}}{6}\tag{8}$$
式(7)、式(8)を式(1)に代入すると、
$$\ddot{u}_{n+1}=-\frac{A・\ddot{u}_n+B・\dot{u}_n+C・u_n+\ddot{u}_{Gn+1}}{D}\tag{9}$$
ここに、
$$A=hω_0・Δt+\frac{ω_0^2・(Δt)^2}{3}$$
$$B=2hω_0+ω_0^2・Δt$$
$$C=ω_0^2$$
$$D=1+hω_0・Δt+\frac{ω_0^2・(Δt)^2}{6}$$
式(9)より相対加速度を求め、これを式(7)、式(8)に代入して相対速度および相対変位を求めます。なお、加速度は相対加速度と地震加速度の和 \((\ddot{u}_n+\ddot{u}_{Gn})\) として絶対加速度の値を求めます。また、応答スペクトルは、構造物の各固有周期に対して応答値の最大値をプロットしたものであるので、上記の方法で求めた時刻歴応答値より絶対値の最大値をそれぞれ求めていきます。
線形加速度法のプロシージャ
メインとインプットのプロシージャは、中央差分法と同じですので、線形加速度法の計算部分のみを示します。
線形加速度法の定式化に従って時刻歴応答を計算し、絶対値の最大値を求めています。求めた結果は、ワークシート”応答スペクトル”に書き込んでいます。
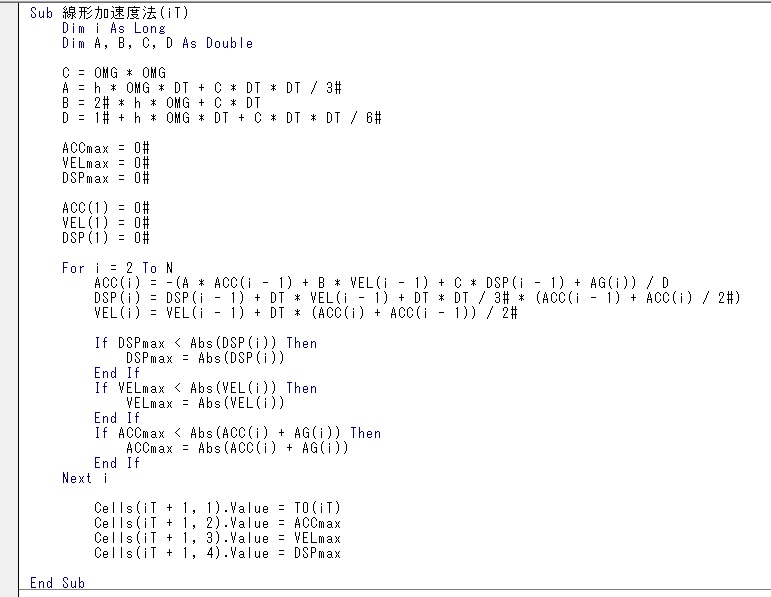
計算結果
下図の地震波に対して、応答スペクトルを算定しました。
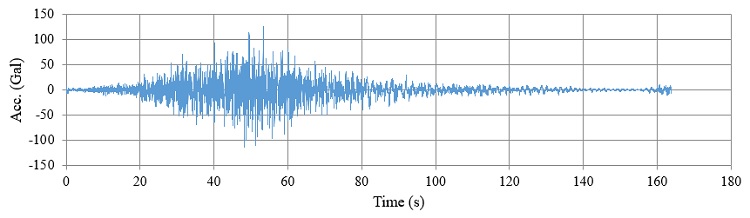
減衰比は0.05、固有周期は0.02~10.00sを100分割しました。
結果はワークシート”応答スペクトル”につぎのように出力され、絶対加速度、相対速度、相対変位をそれぞれグラフ化しています。
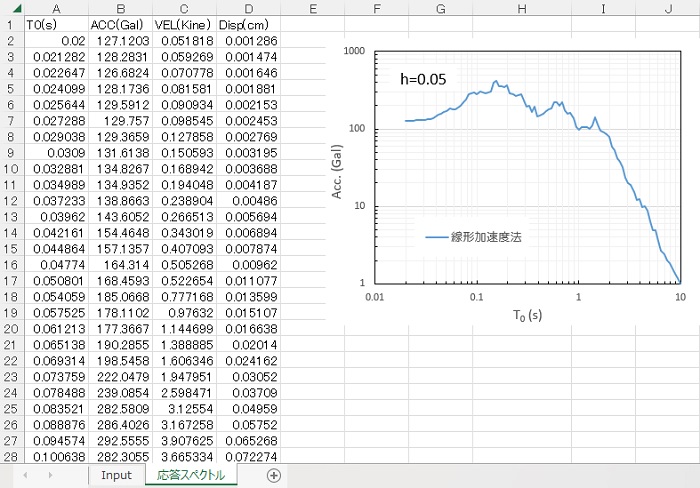
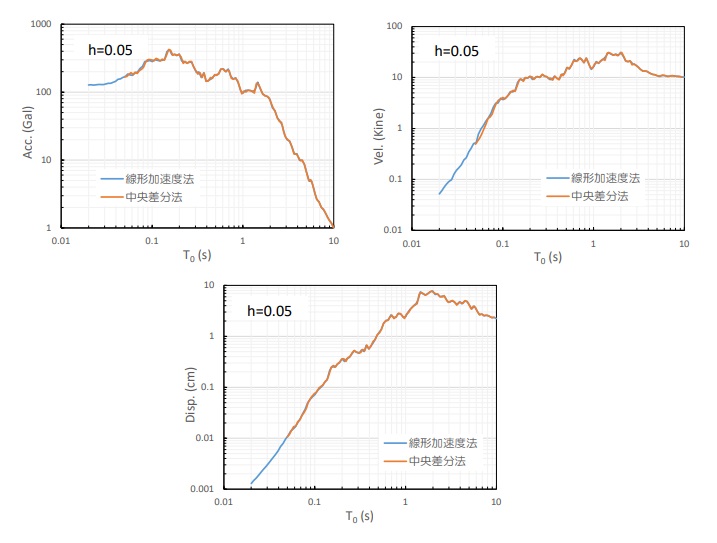
中央差分法と比較した応答スペクトルを示しますが、ほぼ同様な値が得られています。ただし、中央差分法では固有周期が0.05sよりも小さくなるとオーバーフローしてしまっていましたが、線形加速度法では固有周期0.02sまでオーバーフローすること無く計算が可能でした。
以上、参考になれば幸いです。






コメント