ExcelVBAで高速フーリエ変換FFTを作成してみたでFFTのプログラムを紹介しましたが、ここでは高速フーリエ変換のアルゴリズムを考えてみます。
私が学生だった1980年代には、時間領域と振動数領域の変換に当たり前のプログラムとしてFFTが使用されていました。FFT自体のアルゴリズムは1866年のガウスの論文にまでさかのぼるようですが、1965年に発表されたCooley-Tukeyの論文で広く用いられるようになったそうです。
複素フーリエ級数や離散フーリエ変換の性質等については学生時代に勉強しましたが、FFTのアルゴリズムについては深く考えた事がないので、今回学び直しを行いました。
高速フーリエ変換のキモ
つぎの離散フーリエ変換から話を始めます。
$$x[k]=\sum_{n=0}^{N-1}{X[n]e^{-\frac{2πikn}{N}}}\tag{1}$$
ここで、\(W_N=e^{-\frac{2πi}{N}}\)とおけば、
$$x[k]=\sum_{n=0}^{N-1}{X[n]W_N^{kn}}\tag{2}$$
もし、Nが偶数ならN/2は整数なので、
$$W_N^2=e^{-\frac{4πi}{N}}=e^{-\frac{2πi}{(\frac{N}{2})}}=W_{\frac{N}{2}}\tag{3}$$
式(2)を偶数部分と奇数部分に分けて表現すると、
$$x[k]=\sum_{n=0}^{N-1}{X[n]W_N^{kn}}=\sum_{m=0}^{\frac{N}{2}-1}{X[2m]W_N^{2km}}+\sum_{m=0}^{\frac{N}{2}-1}{X[2m+1]W_N^{k(2m+1)}}\tag{4}$$
これに式(3)を代入して整理すると、
$$x[k]=\sum_{m=0}^{\frac{N}{2}-1}{X[2m]W_{\frac{N}{2}}^{km}}+W_{N}^{k}\sum_{m=0}^{\frac{N}{2}-1}{X[2m+1]W_{\frac{N}{2}}^{km}}\tag{5}$$
したがって、もともとの離散フーリエ変換では\(k=N\),\(n=N\)とすると\(N^2\)回の行列計算が必要なのに対して、偶数部と奇数部の2回×\((N/2)^2=\frac{N^2}{2}\)となり、計算回数が\(1/2\)回に減ります。
さらに、\(W_{N}^{k}\)は\(k>N/2の\)とき、\(W_{N}^{\frac{N}{2}+l}=-W_{N}^{l}\)です。\(N\)が2の\(n\)乗であれば、式(5)の操作を\(n\)回実施することで、皆さんがご存じの下図に示すバタフライ演算になります。このときの計算回数は、式(5)の操作を実施するたびに離散フーリエ変換部分の計算が\(1/2\)倍になり、その計算部分が\(n\)段階実施することになるので、\(N^2・n/2^n=N^2・n/N=Nn\)の計算回数となります。\(N=2^n\)なので、\(\log_{2}{N}=n\)となり、計算回数は\(N^2\)回から\(N\log_{2}{N}\)回に減ります。
なお、バタフライ演算における\(x[n]\)の配列は、偶数部と奇数部とに繰り返し配置換えした位置に移動しています。
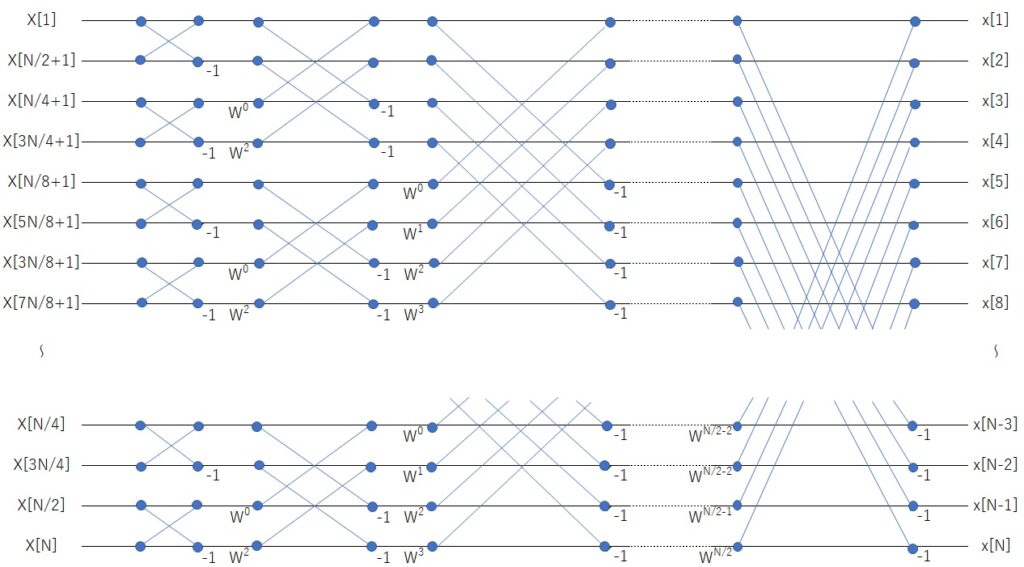
上記のバタフライ演算の一部を取り出したのが下図です。例えば、\(x[1]\)の計算は\(X[1]+W^0・X[3]\)、\(x[3]\)の計算は\(X[1]-W^0・X[3]\)を実施することを意味し、これを上図の左側から順次繰り返していきます。
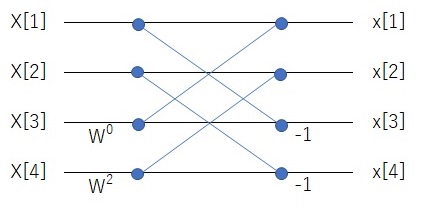
\(x[n]\)の配列はどうなる
バタフライ演算のためには、\(x[n]\)の配列操作が必要となりますが、具体的にどのような配列操作になるのでしょうか?また、最初の配列位置と移動後の配列位置にある数値は、互いに1対1の配置換え(つまり、最初の配列位置にある数値と移動後の配列位置にある数値を入れ替えれば良いのか)になるのでしょうか?
では、具体的に配列を奇数列と偶数列に入れ替えていきます。下表で\(x[n]\)の配列の右側の欄は、その和が最初の配列番号になるようにN/2,N/4~4,2,1の数値の和で表したものです。つまり、2進数の和として示しています。ただし、Fortranのプログラムを用いましたので、配列が1からNまでとなるために、2進数の和に一番右側の欄にて1を加えています。
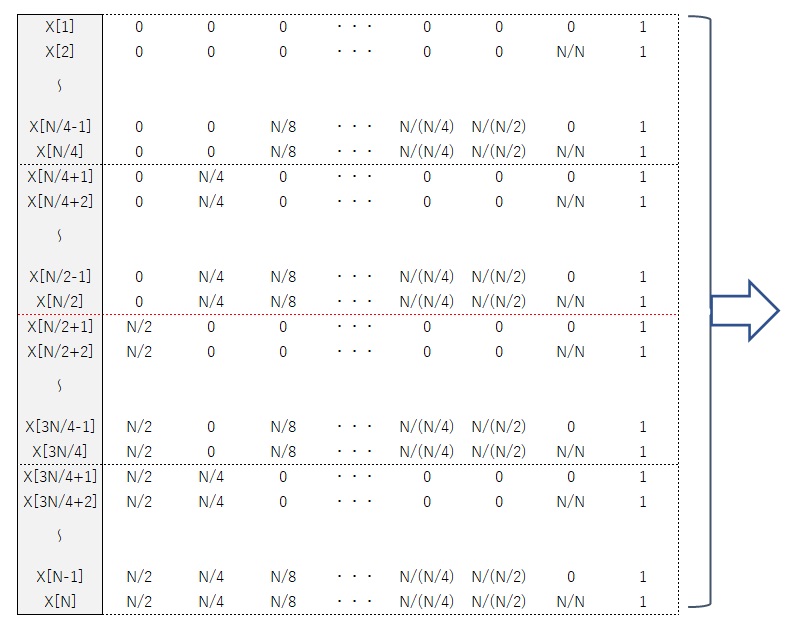
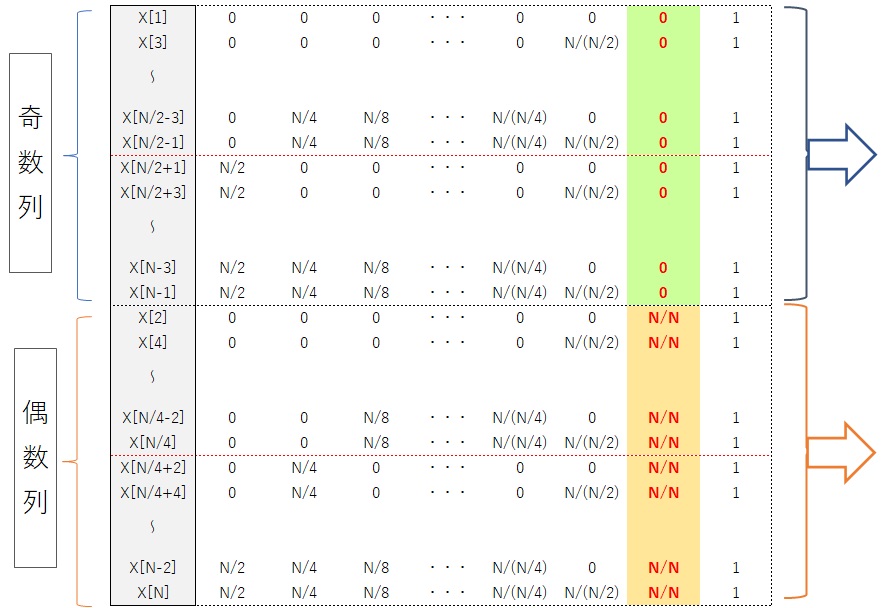
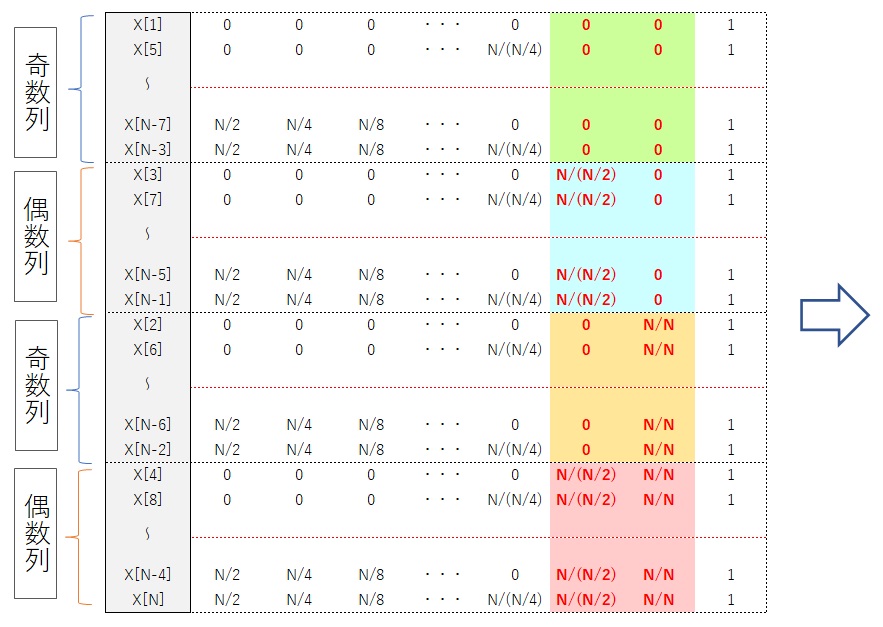
最終的にはつぎのような配列に変換されます。
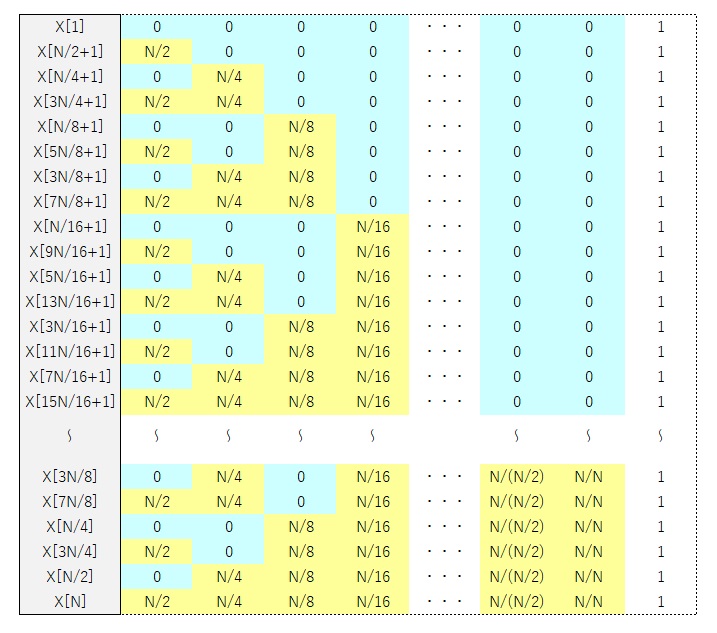
これを2進数の数値として表すとつぎのようになります。
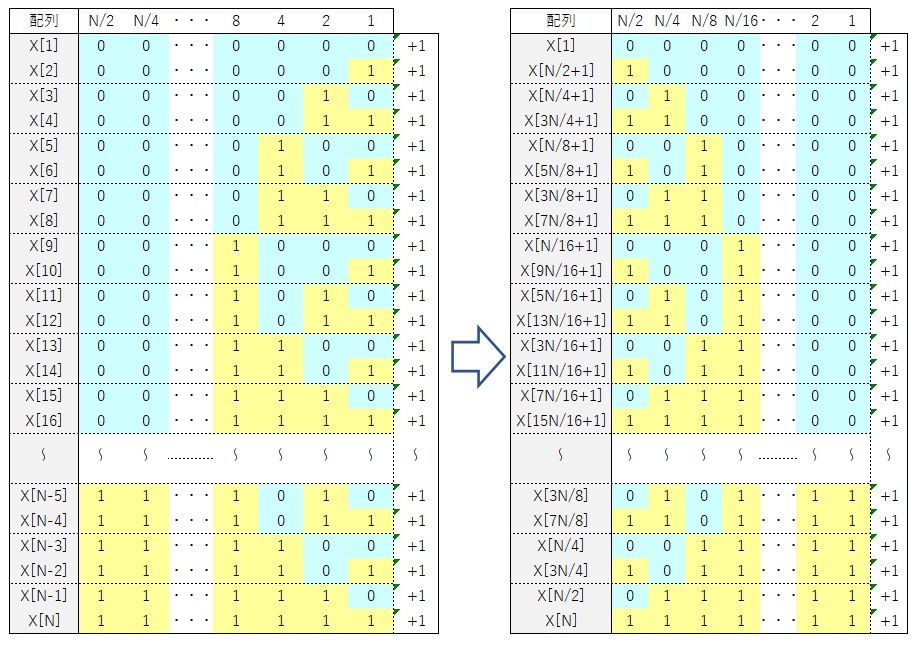
変換前の配列番号を2進数で表すと上位の桁から半分ずつ0と1が並び、つぎの桁では1/4ずつ0と1が、そのつぎの桁は1/8ずつ0と1というように配列されていき、1桁目では0と1が交互に現あわれます。2進数を順番に並べると当然ですね。
つぎに最終的に並び替えた数値を見てみると、1桁目は半分ずつ0と1が並び、つぎの桁では1/4ずつ0と1が、そのつぎの桁は1/8ずつ0と1というように配列されていき、最上位の桁では0と1が交互に現あわれます。これも当然で、奇数部と偶数部に分けていきますので、1桁目から順番に分割された配列毎に0と1が並んでいくわけです。
ここで、変換前の配列と最終的な配列を見ると、2進数の数字がそのまま反転されていることに気づきます。したがって、変換前の配列位置と変換後の配列位置は必ず1つに決まることになり、変換前の配列位置にある数値と変換後の配列位置にある数値を入れ替えれば良いことになります。
まとめ
高速フーリエ変換のアルゴリズムを勉強しました。データ数が\(N=2^n\)個であれば、離散フーリエ変換の行列計算を奇数部と偶数部に分ける変換を\(n\)回繰り返すことができ、計算回数を\(N^2\)回から\(N\log_{2}{N}\)回に減らすことが可能になります。
プログラム計算では、数値データの配列を変換する操作が必要となりますが、0~N-1の配列番号を2進数で表した場合、それを左右反転した数字の配列番号が入れ替わる配列位置となります。
改めて、ExcelVBAで高速フーリエ変換FFTを作成してみたのFFTプログラムを見ていただけると、実際にこの操作を忠実に実行していることが分かります。


コメント