ExcelVBAでモンテカルロシミュレーション(MCS)を実施してみました。壁体の滑動問題を例題に、破壊確率(滑動する確率)をExcelVBAで正規分布乱数を生成してヒストグラムと基本統計量をチェックで作成した正規乱数を元に計算しています。最後に、200万回程度の計算を実行した結果を、FORMから求めた破壊確率と比較しています。
例題:壁体の滑動問題
下図に示す壁体の滑動問題を例題とします。滑動抵抗は重量と摩擦係数の積(X1・X3)、滑動水平力をX2とすると、滑動抵抗>滑動水平力のとき、壁体は滑り出すことになります。
したがって、性能関数 Z=X1・X3 – X2 と定義でき、Z<0のとき破壊(滑動する)すると判定されます。なお、X1,X2,X3は互いに独立な正規確率変数として、下図のように設定します。

MCSのプロシージャ
モンテカルロシミュレーション(MCS)
ここでは、モンテカルロシミュレーションとしてCrude Monte Carloを用います。一様乱数を発生させ、それを確立分布に従う乱数に変換し、性能関数により破壊か安全かを判定してきます。そして、破壊の回数を試行回数で割ったものを破壊確率とします。試行回数は、破壊確率の変動係数が1%程度まで小さくなる回数を実施します。
プロシージャの内容
計算内容は以下のようです。
- 一様乱数の初期200回分を空読み
- Excelシートから、各変数の平均と標準偏差を読み込み
- Excelシートから、各試行回数とそれを何回繰り返すかを読み込み
- 正規確率乱数から性能関数を計算し、ゼロ以下になる回数を求める
- 試行回数(dnum)ごとに破壊確率をExcelシートに出力
- 最終破壊確率(num×dnum回目)をExcelシートに出力

計算の実行
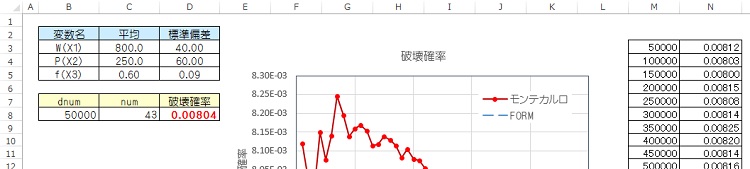
入力データは、ExcelシートのセルC3~D5、B8,C8に試行回数を記入しておきます。
計算を実行すると、M列とN列のセルに試行回数と破壊確率が出力されます。最終の破壊確率値は、D8のセルに出力されます。
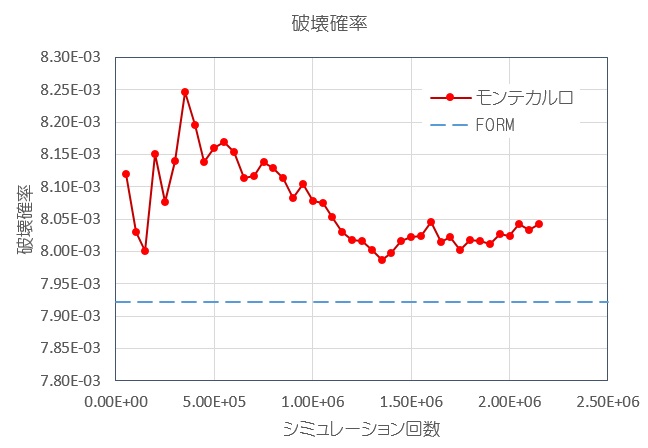
モンテカルロシミュレーションの収束状況
出力結果から、モンテカルロシミュレーション結果を描いたグラフです。1500,000回ぐらいから、破壊確率の約1%程度の範囲を変動していますので、破壊確率は0.00800~0.00805程度と得られました。
このモンテカルロシミュレーションの結果は、乱数の初期値(空読みの個数や実施日)を変えることで、違った動きになることに注意が必要です。
なお、FORMで算定した結果が破壊確率0.00792ですので、若干の差が見られますが、8×10-3程度の破壊確率と見れば正しく解が得られたと考えられます。
まとめ
ExcelVBAでモンテカルロシミュレーションを実施し、壁体の滑動の破壊確率を算定しました。FORMと有効数字2桁目で若干の差が出ており、その要因については明確ではありませんが、ほぼ妥当な解が得られたものと思われます。
なお、Pythonでモンテカルロシミュレーション【滑動に関する信頼性解析】において、Pythonで同様な解析を実施していますが、ほぼ同様な傾向が得られていますので、興味のある方はご参照ください。



コメント