弾性波伝播の特定の問題を解析する場合、直交曲線座標は数学的処理の単純化につながることがよくあります。適切に選択された曲線座標系において、座標の 1 つが物体の境界面上で一定である場合、簡略化が実現します。たとえば、境界のない媒質内の半径 \(a\) の球状キャビティから発せられる波の場合、キャビティの表面上の強制条件は、単純に \(r=a\) で規定される球面座標になります。
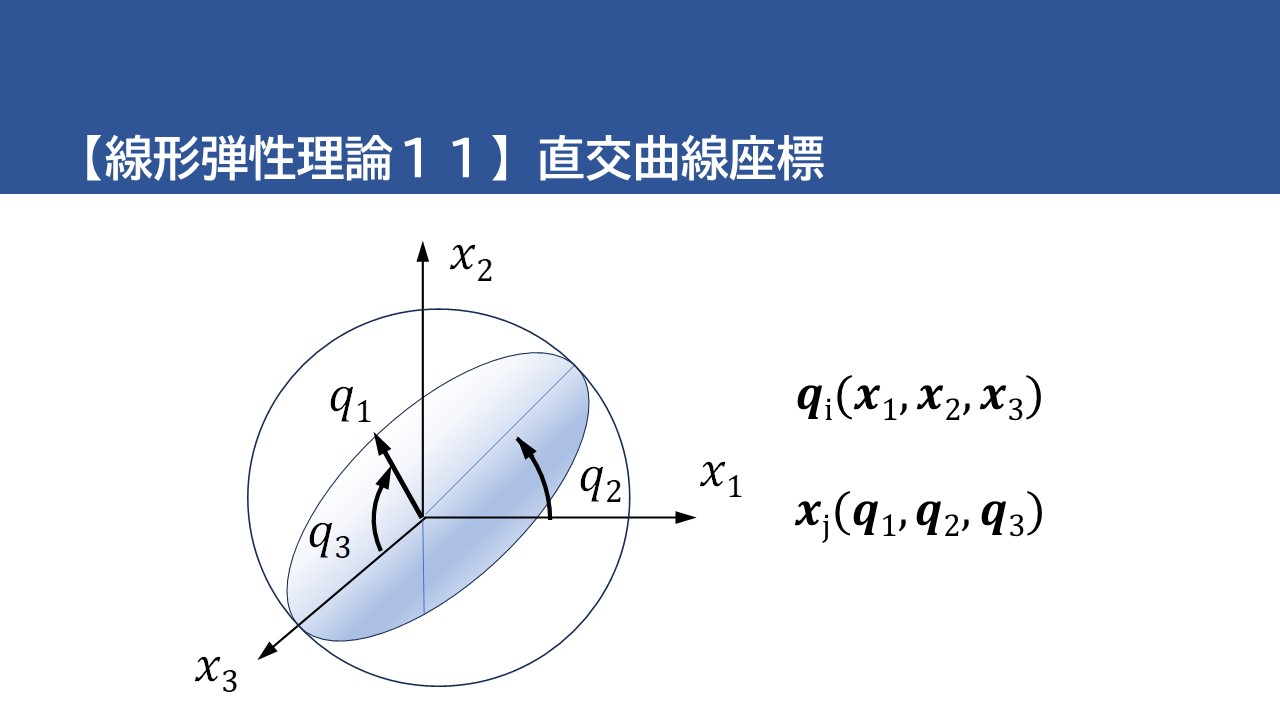
一般的なテンソル計算により、あらゆる次元の非直交曲線座標系を扱うことができます。 ただし、ここでは議論を 3 次元直交曲線座標に限定します。 デカルト変数 \(x_j\) の独立関数 \(q_i\) のセットを考えてみましょう。
$$q_i=q_i (x_1 , x_2 , x_3)\tag{114}$$
そして、これらの方程式が \(q_i\) に関して \(x_j\) について解けると仮定しましょう。または、
$$x_j=x_j (q_1 , q_2 , q_3)\tag{115}$$
3 つの方程式 \(q_i=c_i \) (\(c_i\) は定数) は、3 つの曲面ファミリーを表し、その交線が 3 つの曲線ファミリーを形成します。これらの交線は、曲線座標系の座標線として使用されます。 したがって、空間内の点の位置は、3 つの座標 \(q_1\) , \(q_2\) , \(q_3\) の値によって定義できます。ある点におけるローカル座標方向は、その点で交差する 3 本の座標線に接します。
このセクションで考慮する直交座標系では、3 つの座標方向は相互に直交します。それぞれ座標 \(q_1\) , \(q_2\) , \(q_3\) の増加方向に取った単位ベクトル \(e_1\) , \(e_2\) , \(e_3\) を正規直交右手系で定義します。 次のよく知られた関係が成り立ちます。
$$e_i・e_j =δ_{ij}\tag{116}$$
$$e_i∧e_j =e_k\tag{117}$$
ここで、式(117)において、インデックス \(i\) , \(j\) , \(k\) は巡回順序になっています。曲線座標とデカルト座標の主な違いは、座標 \(q_1\) , \(q_2\) , \(q_3\) が必ずしも長さで測定されるわけではないことです。 たとえば、円筒座標では \(q_1=r\) , \(q_2=θ\) , \(q_3=x_3\) となります。 この違いは、微小変位ベクトル \(d\mathbf{r}\) と微小変化 \(dq_1\) , \(dq_2\) , \(dq_3\) の間の関係におけるスケール係数の出現として現れ、
$$d\mathbf{r}=e_1h_1dq_1+e_2h_2dq_2+e_3h_3dq_3\tag{118}$$
スケール係数 \(h_i\) は一般に座標 \(q_j\) の関数です。
単位ベクトル \(e_i\) は一般に空間内の点から点へと方向が変化するため、単位ベクトル \(e_i\) の偏導関数 \(\partial /\partial q_j\) を注意深く調べる必要があります。 \(d\mathbf{r}\) の式(118) から、次のようになります。
$$\frac{\partial \mathbf{r}}{\partial q_i}=e_i h_i$$
\(\partial^2 \mathbf{r}/\partial q_1\partial q_2\) では微分の順序が変わる可能性があるので、
$$\frac{\partial }{\partial q_1}(e_2h_2)=\frac{\partial }{\partial q_2}(e_1h_1)$$
または
$$e_2\frac{\partial h_2}{\partial q_1}+h_2\frac{\partial e_2}{\partial q_1}=e_1\frac{\partial h_1}{\partial q_2}+h_1\frac{\partial e_1}{\partial q_2}\tag{119}$$
\(e_1\) とスカラー積を取ると、次のようになります。
$$h_2e_1\frac{\partial e_2}{\partial q_1}=\frac{\partial h_1}{\partial q_2}\tag{120}$$
ここで、式(116) を使用し、直交システムでは \(e_1・(\partial e_1/\partial q_2)=0\) であるという事実も使用します。式(119) に \(e_3\) をスカラー的に乗算すると次のようになります。
$$h_2e_3・\frac{\partial e_2}{\partial q_1}=h_1e_3・\frac{\partial e_1}{\partial q_2}\tag{121}$$
指示の順列により、式(121) に類似した 2 つの式が次のように見つかります。
$$h_3e_1・\frac{\partial e_3}{\partial q_2}=h_2e_1・\frac{\partial e_2}{\partial q_3}\tag{122a}$$
$$h_1e_2・\frac{\partial e_1}{\partial q_3}=h_3e_2・\frac{\partial e_3}{\partial q_1}\tag{122b}$$
ここで、\(q_1\) , \(q_2\) , \(q_3\) についてそれぞれ \(e_3・e_2=0\) , \(e_1・e_2=0\) , \(e_1・e_3=0\) を導出し、その結果の方程式と式 (122a,b) を使用すると、次のようになります。 次の操作は直接検証可能です。
$$e_3・\frac{\partial e_2}{\partial q_1}=-e_2・\frac{\partial e_3}{\partial q_1}=-\frac{h_1}{h_3}e_2・\frac{\partial e_1}{\partial q_3}=\frac{h_1}{h_3}e_1・\frac{\partial e_2}{\partial q_3}$$
$$=\frac{h_1}{h_2}e_1・\frac{\partial e_3}{\partial q_2}=-\frac{h_1}{h_2}e_3・\frac{\partial e_1}{\partial q_2}=-e_3・\frac{\partial e_2}{\partial q_1}$$
結果は、 \(e_3\) と \(\partial e_2/\partial q_1\) の内積が消失することを示し、\(e_2\) と \(\partial e_2/\partial q_1\) の内積は消失すると結論付けられ、 \(\partial e_2/\partial q_1\) には \(e_2\) と \(e_3\) の方向の成分がないと結論付けられます。 式(120) から次のことがわかります。
$$\frac{\partial e_2}{\partial q_1}=\frac{e_1}{h_2}\frac{\partial h_1}{\partial q_2}$$
この形式の他の 5 つの関係は、インデックスの順列によって導出でき、6 つの結果は次のように要約できます。
$$i≠j: \frac{\partial e_i}{\partial q_j}=\frac{e_j}{h_i}\frac{\partial h_j}{\partial q_i} (no\enspace summation)\tag{123}$$
式(117) を使用すると、次のように書くこともできます。
$$\frac{\partial e_1}{\partial q_1}=\frac{\partial }{\partial q_1}(e_2∧e_3)=e_2∧\frac{\partial e_3}{\partial q_1}-e_3∧\frac{\partial e_2}{\partial q_1}=-\frac{e_3}{h_3}\frac{\partial h_1}{\partial q_3}-\frac{e_2}{h_2}\frac{\partial h_1}{\partial q_2}$$
\(\partial e_2/\partial q_2\) と \(\partial e_3/\partial q_3\) に対して 2 つの同様の式を導き出すことができます。 指標表記では次のようになります。
$$\frac{\partial e_i}{\partial q_i}=-\frac{e_j}{h_j}\frac{\partial h_i}{\partial q_j}-\frac{e_k}{h_k}\frac{\partial h_i}{\partial q_k} (no\enspace summation)\tag{124}$$
ここで、\(i\) , \(j\) , \(k\) は巡回順序で取得する必要があります。
空間導関数を含まず、ある点の特性に関係するデカルト座標の方程式はすべて、変更されずに曲線座標に引き継がれます。ただし、空間導関数が関与する場合、勾配、発散、カール、ラプラシアンなどの微分演算子が異なる形式をとるため、方程式は直接引き継がれません。
まず勾配演算子 \(\mathbf{∇}\) を考えます。スカラー \(φ\) に適用すると、 \(f_1\) , \(f_2\) , \(f_3\) と呼ばれる成分を持つベクトル \(\mathbf{∇}φ\) が得られます。 したがって、
$$\mathbf{∇}φ=f_1e_1+f_2e_2+f_3e_3$$
位置の変化 \(dr\) による \(φ\) の増分は、
$$dφ=\mathbf{∇}φ・d\mathbf{r}=h_1f_1dq_1+h_2f_2dq_2+h_3f_3dq_3$$
ここで式(118)が使用されています。増分 \(dφ\) は次のように書くこともできます。
$$dφ=\frac{\partial φ}{\partial q_1}dq_1+\frac{\partial φ}{\partial q_2}dq_2+\frac{\partial φ}{\partial q_3}dq_3$$
したがって、つぎのように結論付けることができます。
$$\mathbf{∇}=\frac{e_1}{h_1}\frac{\partial }{\partial q_1}+\frac{e_2}{h_2}\frac{\partial }{\partial q_2}+\frac{e_3}{h_3}\frac{\partial }{\partial q_3}\tag{125}$$
演算式(125)をベクトル \(\mathbf{u}\) に適用すると、次のようになります。
$$\mathbf{∇u}=\frac{e_1}{h_1}\frac{\partial \mathbf{u}}{\partial q_1}+\frac{e_2}{h_2}\frac{\partial \mathbf{u}}{\partial q_2}+\frac{e_3}{h_3}\frac{\partial \mathbf{u}}{\partial q_3}\tag{126}$$
これは、式(123) と 式(124) を使用してさらに詳細に書き出すことができます。ベクトル \(\mathbf{u}\) の発散は次のとおりです。
$$div\mathbf{u}=\mathbf{∇}・mathbf{u}=\mathbf{∇}・(u_1e_1+u_2e_2+u_3e_3)$$
$$=\mathbf{∇}・(u_1e_1)+\mathbf{∇}・(u_2e_2)+\mathbf{∇}・(u_3e_3)\tag{127}$$
\(q_i\) は独立した座標なので、式(125) を使用して求めます。
$$\mathbf{∇}q_i=\frac{e_i}{h_i} (no\enspace summation)\tag{128}$$
\(\mathbf{∇}q_1\) と \(\mathbf{∇}q_2\) のベクトル積を書くと、次のことがわかります。
$$e_i=h_jh_k\mathbf{∇}q_j∧\mathbf{∇}q_k (no\enspace summation)$$
ここで、\(i\) , \(j\) , \(k\) は巡回順序です。この結果を \(i=1\) , \(j=2\) , \(k=3\) として 式(127) の最初の値に代入すると、次のようになります。
$$\begin{multline}\mathbf{∇}・(u_1e_1)=∇(u_1h_2h_3)・(\mathbf{∇}q_2∧\mathbf{∇}q_3)+u_1h_2h_3\mathbf{∇}・(\mathbf{∇}q_2∧\mathbf{∇}q_3)\\
=∇(u_1h_2h_3)・\Bigl(\frac{e_1}{h_2h_3}\Bigr)+0=\frac{1}{h_1h_2h_3}\frac{\partial }{\partial q_1}(u_1h_2h_3)\end{multline}$$
他の 2 つの項も同様の方法で計算できます。
$$\mathbf{∇}・\mathbf{u}=\frac{1}{h_1h_2h_3}\Bigr[\frac{\partial }{\partial q_1}(u_1h_2h_3)+\frac{\partial }{\partial q_2}(u_2h_3h_1)+\frac{\partial }{\partial q_3}(u_3h_1h_2)\Bigl]\tag{129}$$
ベクトル \(\mathbf{u}\) のカール演算子は式(128)を使って次のとおりです。
$$\mathbf{∇}∧\mathbf{u}=\mathbf{∇}∧(u_1h_1\mathbf{∇}q_1)+\mathbf{∇}∧(u_2h_2\mathbf{∇}q_2)+\mathbf{∇}∧(u_3h_3\mathbf{∇}q_3)$$
スカラーとベクトルの積のカールに関する規則を使用することにより、最初の項は次のようになります。
$$\mathbf{∇}∧(u_1h_1\mathbf{∇}q_1)=\frac{e_2}{h_3h_1}\frac{\partial }{\partial q_3}(u_1h_1)-\frac{e_3}{h_2h_1}\frac{\partial }{\partial q_2}(u_1h_1)$$
他の 2 つの項も同様の方法で計算できて、
$$ \mathbf{∇}∧\mathbf{u}= \frac{1}{h_1h_2h_3}\begin{vmatrix} h_1e_1&h_2e_2&h_3e_3\\\frac{\partial }{\partial q_1}&\frac{\partial }{\partial q_2}&\frac{\partial }{\partial q_3}\\ h_1u_1 & h_2u_2 & h_3u_3\end{vmatrix} \tag{130}$$
スカラーのラプラス演算子は、式(129)と式(125)を使用して簡単に導出できます。
$$\mathbf{∇}^2φ=\mathbf{∇}・\mathbf{∇}φ=\frac{1}{h_1h_2h_3}\sum_{i=1}^3 \frac{\partial }{\partial q_n}\Bigr[\frac{h_1h_2h_3}{h_n^2}\frac{\partial φ}{\partial q_n}\Bigl]\tag{131}$$
ベクトルのラプラシアンはさらに複雑なので、式は書きませんが、次のことを使用すると、
$$\mathbf{∇}^2\mathbf{u}=\mathbf{∇}(\mathbf{∇}・\mathbf{u})-\mathbf{∇}∧\mathbf{∇}∧\mathbf{u}$$
ベクトルのラプラシアンはさらに複雑なので、式は書きません。 ただし、次式を使用し、勾配、発散、カールの式を使用することによって、\(\mathbf{∇}^2\mathbf{u}\) を取得できます。


コメント