2次元問題
2 次元問題では、物体の力と応力テンソルの成分は、座標の 1 つ、たとえば \(x_3\) から独立しています。応力の運動方程式は、\(\partial{}/\partial{x_3}≡0\) と設定することで 式(39) から導出できます。その結果 2 つの独立な方程式に分割され、
$$τ_{3β,β}+ρf_3=ρ\ddot{u}_3\tag{52}$$
$$τ_{αβ,β}+ρf_α=ρ\ddot{u}_α\tag{53}$$
式(52)と式(53)、およびこのセクション全体を通じて、ギリシャ文字の添字は1と2のみを取ることができます。
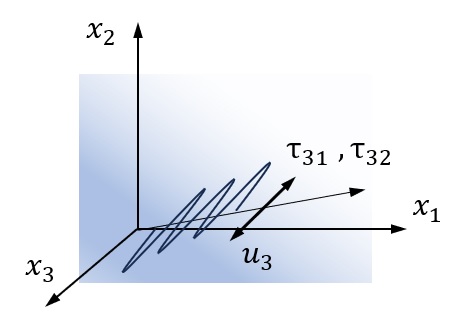
面外せん断
変位分布 \(u_3(x_1,x_2,t)\) で記述される変形は、面外せん断変形と呼ばれます。対応する応力成分はフックの法則から次のようになります。
$$τ_{3β}=μu_{3,β}\tag{54}$$
式(52)および式(54)から \(τ_{3β}\) を消去すると、\(u_3(x_1,x_2,t)\) がつぎのスカラー波動方程式によって表わされることがわかります。
$$μu_{3,ββ}+ρf_3=ρ\ddot{u}_3\tag{55}$$
式(55)で示される単純せん断運動は一般にSH波(horizontally polarized shear motions)と呼ばれます。
面内運動
式(53)は面内変位 \(u_α\) が \(x_1\),\(x_2\) と \(t\) のみに依存する事がわかります。\(u_3\) の空間座標と時間への依存性に関して、式(53)からはつぎの2つのケースが記述されます。
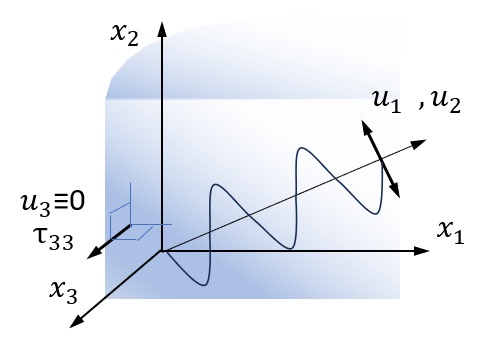
平面ひずみ
平面ひずみの変形では、すべての場の変数は \(x_3\) から独立しており、\(x_3\) 方向の変位は同様に消滅します。フックの法則により、次の関係が得られます。
$$τ_{αβ}=λu_{γ,γ}δ_{αβ}+μ(u_{α,β}+u_{β,α})\tag{56}$$
$$τ_{33}=λu_{γ,γ}\tag{57}$$
ここで、ギリシャ文字の添字は1と2のみを取ることが出来ます。
式(53)と式(56)から \(τ_{αβ}\) を消去すると、
$$μu_{α,ββ}+(λ+μ)u_{β,βα}+ρf_α=ρ\ddot{u}_α\tag{58}$$
式(58)は式(42)から \(u_3≡0\) と \(\partial{}/\partial{x_3}≡0\) とすることでも直接導かれます。
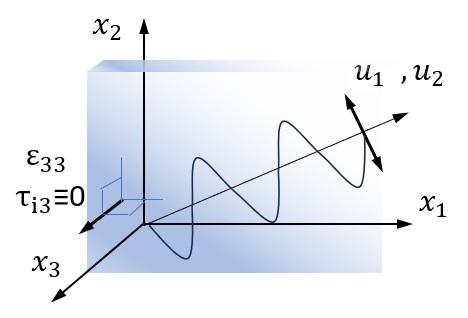
平面応力
\(τ_{33}\),\(τ_{23}\),\(τ_{13}\) をゼロとする2次元応力状態は平面応力と呼ばれます。フックの法則から \(ε_{33}\) と \(ε_{11}+ε_{22}\) の関係が次のように導かれます。
$$ε_{33}=-\frac{λ}{λ+2μ}u_{γ,γ}\tag{59}$$
式(59) を \(τ_{αβ}\) の式に代入すると、
$$τ_{αβ}=\frac{2μλ}{λ+2μ}u_{γ,γ}δ_{αβ}+μ(u_{α,β}+u_{β,α})\tag{60}$$
式(60)を式(53)に代入すると変位の運動方程式が得られます。支配方程式に関する限り、平面ひずみと平面応力の違いは、定数係数の違いにすぎません。 式(59) は、座標 \(x_3\) に対する \(u_3\) の線形依存性を示していることに注意してください。平面応力のケースは、薄いシートの面内運動の近似的な説明によく使用されます。
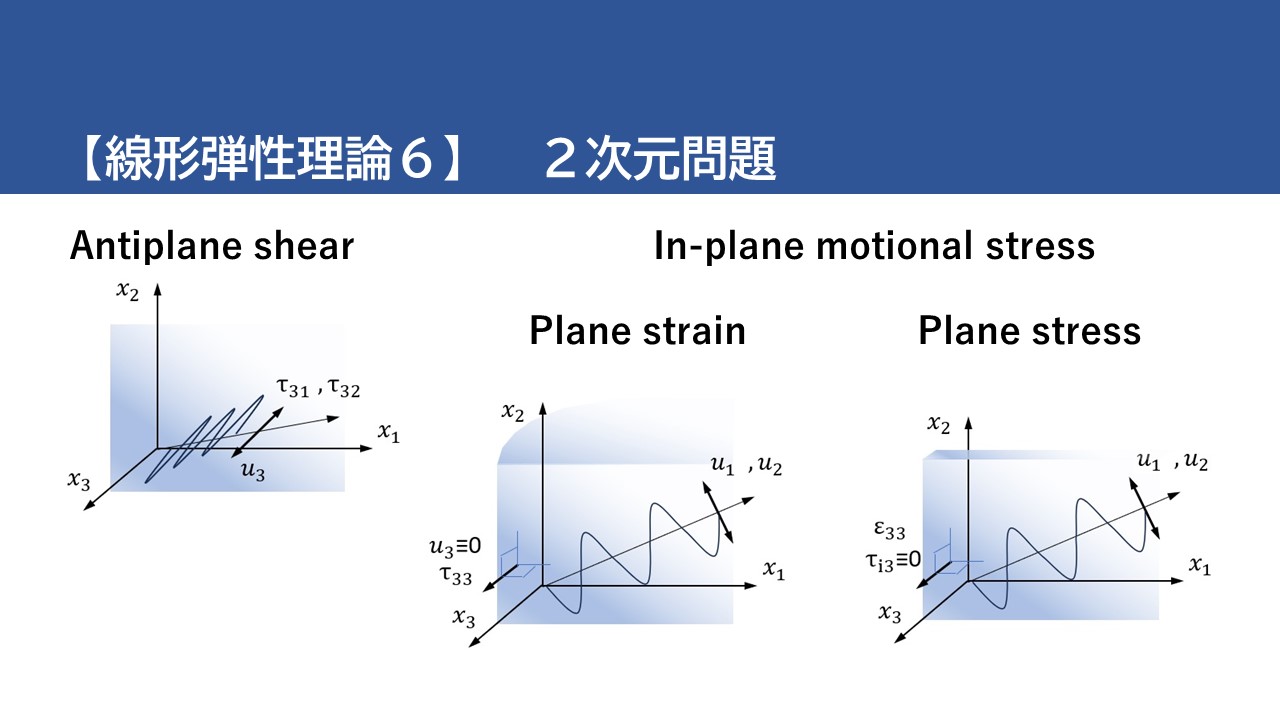
これらの結果は、二次元波動が面外運動と面内運動の重ね合わせであることを示しており、これらの運動は非連成方程式によって支配されます。
今回は以上です。


コメント