モリソン(Morison)式により海中部材に作用する最大波力と最大モーメントを算定するプロシージャを作成していきます。
第1回目は波力算定上の仮定、算定方法と各算定式の説明です。
波力算定上の仮定と算定式
波力算定上の仮定は以下のようです。
- モリソン式を用いる(海中の杭のように波長に比べて断面が小さいものを対象とする)
- 水粒子の速度及び加速度は微小振幅波として求める
- ウェーラのストレッチ理論を用いる(波力を算定する海面までの高さに対応する水粒子速度及び加速度の算定高さを同式で設定)
つぎからそれぞれの算定式を示します。
モリソン式
海中にある杭のように波長に比べてその径が小さいものは、波の進行をほとんど阻止することがなく、次のモリソン式で波力を算定することができる。
$$f_n=\frac{1}{2}C_D ρ_0|u_n|u_nDΔS+C_M ρ_0 a_nAΔS\tag{1}$$
ここに、 \(f_n\) :微小長さ\(ΔS\)に作用する軸直角方向の力(kN)
\(u_n\) :部材軸直角方向の水粒子速度(m/s)
\(|u_n|\) :部材軸直角方向の水粒子速度の絶対値(m/s)
\(a_n\) :部材軸直角方向の水粒子加速度(m/s2)
\(C_D\) :抗力係数
\(C_M\) :慣性力係数
\(D\) :部材軸直角方向の部材幅(m)
\(A\) :部材軸直角方向の部材断面積(m2)
\(ρ_0\) :海水の密度(t/m3)
水位の上昇量と水粒子速度・加速度
微小振幅波理論が適応可能な条件に限定し、次式により水位の上昇量と水粒子速度と加速度を算定する。
$$η=\frac{H}{2}cos(kx-ωt)\tag{2}$$
$$u_n=\frac{H}{2}ω\frac{cosh(kz)}{sinh(kh)}cos(kx-ωt)\tag{3}$$
$$a_n=\frac{H}{2}ω^2\frac{cosh(kz)}{sinh(kh)}sin(kx-ωt)\tag{4}$$
ここに、 \(η\):静水面からの水位の上昇量(m)
\(u_n\):水粒子速度の水平成分(m/s)
\(a_n\):水粒子加速度の水平成分(m/s2)
\(k\):波数(1/m),\(k=\frac{2π}{L}\)
\(L\):水深hにおける波長(m)
\(ω\):各周波数(rad/s),\(ω=\frac{2π}{T_D}\)
\(T_D\):設計波周期(s)
\(t\):時間(s)
\(x\):波の進行方向にとった水平座標値(m)
\(z\):海底面から鉛直上向きを正とした鉛直座標値(m)
ただし、今回は波力の最大値、波力によるモーメントの最大値を算定することを目的としたプロシージャを作成するため、\(kx-ωt\)を位相角として0~360°までの変数として扱い、最大値を探していきます。
ウェーラのストレッチ理論
式(2),(3),(4)の微小振幅波理論では、水面変動の影響を考慮していない座標\(z\)に関して水粒子速度・加速度を算定する。しかし、部材に作用する波力は、水位変動量を考慮した座標まで水粒子の運動が作用する。
ここでは、この効果を考慮するために、ウェーラのストレッチ理論を用いる。
$$z=\frac{z_s}{h+η}・h\tag{5}$$
ここに、 \(z\):微小振幅波理論を適用する鉛直座標(m),\(\small0≤z≤h\)
\(z_s\):水粒子速度、加速度を作用させる鉛直座標(m),\(\small0≤z≤h+η\)
\(h\):水深(m)
\(η\):静水面から測った海面高(m)
なお、今回の計算では、部材に作用する波力を算定する鉛直座標には\(z_s\)を、微小振幅波で水粒子速度・加速度を計算する際の鉛直座標には\(z\)を使用します。
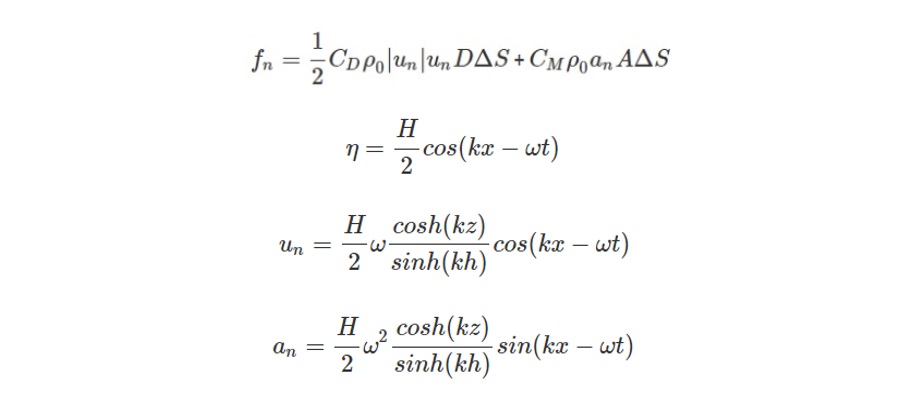


コメント