今回は、まず空間においてはディスク載荷と点載荷を、時間においてはディラックのデルタ関数とへヴィサイド関数を用いた場合の衝撃載荷のモデル化を示します。次いで、ラプラス・波数領域での変位解にこれら衝撃載荷力を採用し、逆ラプラス変換、逆ハンケル変換を実行することによって時間・空間領域での変位解を導いていきます。
衝撃載荷のモデル化
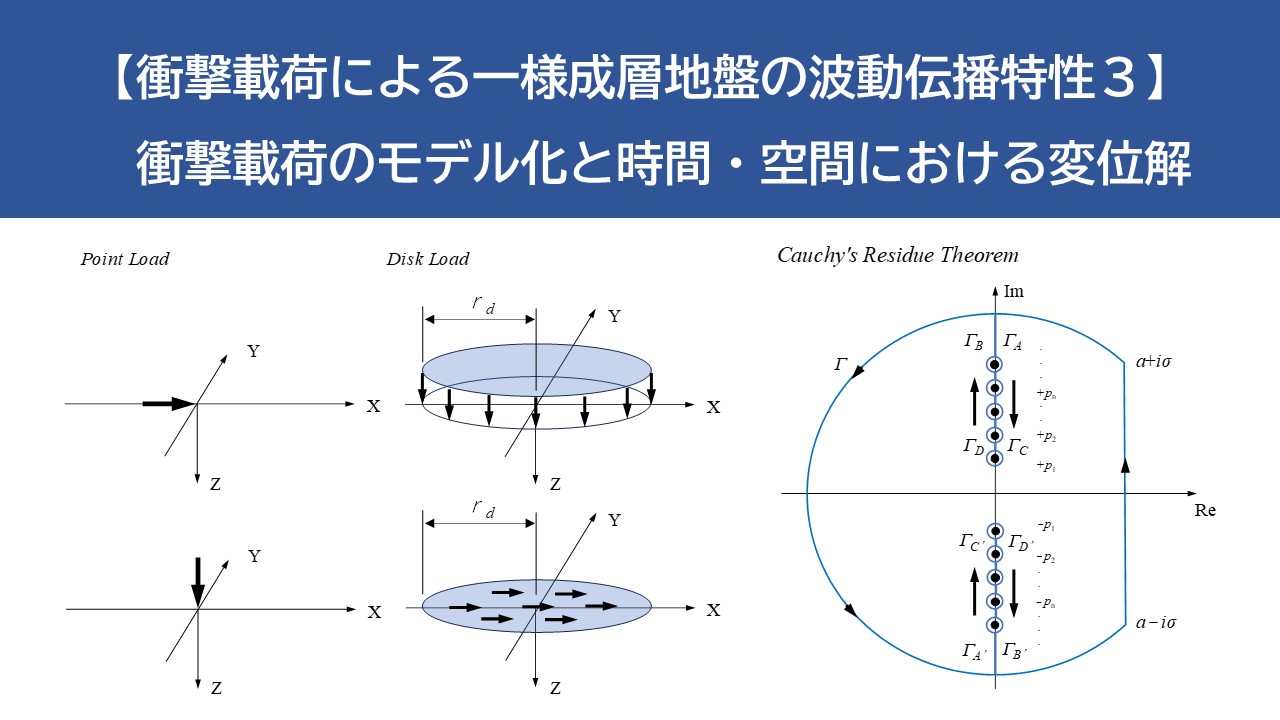
衝撃載荷として点載荷およびディスク載荷のモデル化を行う。これら衝撃載荷の単位力としての表現式は、空間関数 \(Φ_{i}(r,θ)\) と時間関数 \(Γ(t)\) の積として、
$$f_{i}= Φ_{i}(r,θ)・δ(z-H)・Γ(t)\tag{40}$$
ラプラス・波数領域では、
$$\tilde{\bar{f}}_{in}= \tilde{Φ}_{in}(ξ)・δ(z-H)・\bar{Γ}(p)\tag{41}$$
のように表わされる。
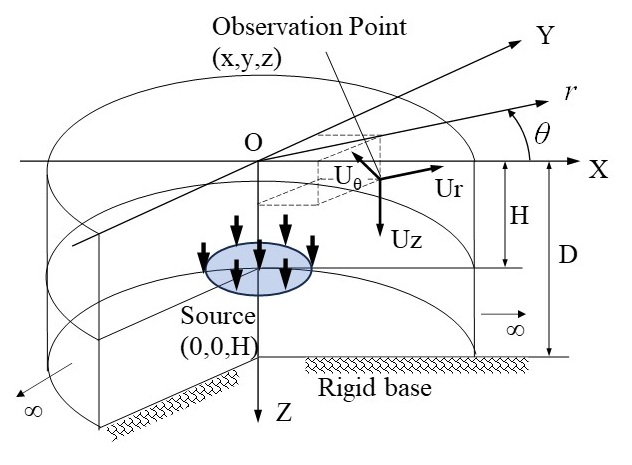
まず空間関数について示す。ディスク載荷は \(XーY\) 平面内の半径 \(r_{d}\) のディスク上に等分布するものとする。フーリエ級数展開による軸対称モデルとして式(8.a)の変換に従えば、ラプラス・波数領域での表現が得られる。点載荷の場合には、ディスク載荷の式において、半径 \(r_{d}\) を0にした場合の極限値を採ればよい。
その結果、点載荷およびディスク載荷ともに、鉛直方向載荷および水平方向載荷(x方向載荷)の2成分が、それぞれ0次、1次のフーリエ級数(軸対称モード)として表現される。下表に、ディスク載荷と点載荷の空間領域での表現および波数領域での表現を示す。
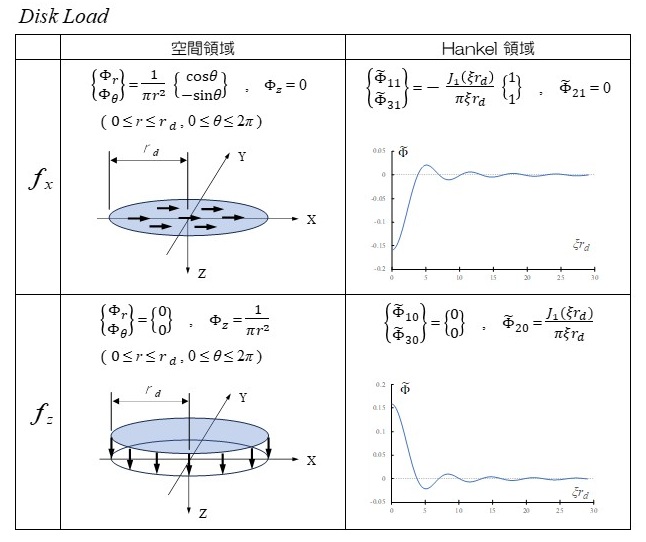
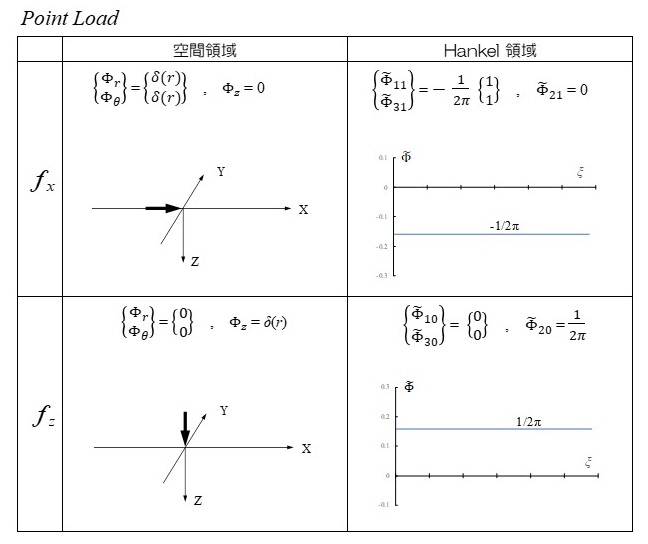
波数領域での空間関数に注目すると、点載荷では波数に関係なく一定値を示すのに対して、ディスク載荷では波数が大きくなると減少する傾向にあり、ディスク半径が大きいほどこの傾向が強まることが分かる。従って、次節に示す波数積分の収束性に関してはディスク載荷モデルが有利である。現実問題での載荷状態では完全な点載荷は起こり難いと考えられることや、ディスク半径のおおよそ7倍以上の距離での変位応答は点載荷と差がなくなることからも、ディスク載荷モデルの応用範囲は広いと言える。なお、y方向載荷に対する変位解はx方向載荷に対するものを座標変換することによって得られるため、ここではx方向載荷のみを示した。
時間関数 \(Γ(t)\) に対しては、ディラックのデルタ関数 \(δ(t)\) として直接定式化する方法と、ヘヴィサイド関数の差 \(\{H(t_{1})-H(t_{2})\}\) によって \(Δt=t_{1}-t_{2}\) 間に作用する荷重として近似的に取り扱う方法がある。それぞれの関数は、ラプラス領域で以下のように表される。
ディラックのデルタ関数 \(δ(t)\) に関して
$$\bar{Γ}(p)=1\tag{42}$$
ヘヴィサイド関数の差 \(H(t)\) に関して
$$\bar{Γ}(p)=\frac{1}{p}\tag{43}$$
時間・空間領域における変位解
ラプラス・波数領域での変位解(式(35)、式(36))に衝撃載荷力式(41)を代入し、逆ラプラス変換(式(3))および逆ハンケル変換(式(7.b))を実行することによって時間・空間領域での変位解が得られる。
まず、逆ラプラス変換はラプラス複素平面状での周回積分法(Bromwitch積分)により解析的に求めることができる。特異点は式(35)、式(36)、式(42)あるいは式(43)より、
$$p=0\tag{44.a}$$
$$p=±p_{i}^{sv-p}=±i|ξ|c_{i} (i=1,2,・・・・)\tag{44.b}$$
$$p=±p_{i}^{sh}=±i|ξ|c_{i} (i=1,2,・・・・)\tag{44.c}$$
が存在する。式(44.b)の根は面内波動場での特性方程式(37)より、式(44.c)の根は面外波動場での特性方程式(38)より得られ、それぞれ上添え字 \(sv-p\) および \(sh\) で示す。これらの根は、任意の波数に対して無限個存在する。特異点のうち、\(p=0\) は初期条件(因果性)を考慮することにより特異性を外すことができ、真の特異性は後者のみである。
また、分岐点は被積分関数の \(k_{α}=0\) , \(k_{β}=0\) より、
$$p=±i|ξ|V_{p}\tag{45.a}$$
$$p=±i|ξ|V_{s}\tag{45.b}$$
Cauchyの留数定理に基づいて、周回積分は次のように実行される。
$$\frac{1}{2πi}\int_{α-i∞}^{α+i}=Res\Bigl[\tilde{\bar{u}}\Bigr]$$
$$-\frac{1}{2πi}\Bigl(\int_{Γ}+\int_{Γ_{A}}+\int_{Γ_{B}}+\int_{Γ_{C}}+\int_{Γ_{D}}+\int_{Γ_{A’}}+\int_{Γ_{B’}}+\int_{Γ_{C’}}+\int_{Γ_{D’}}\Bigr)\tag{46}$$
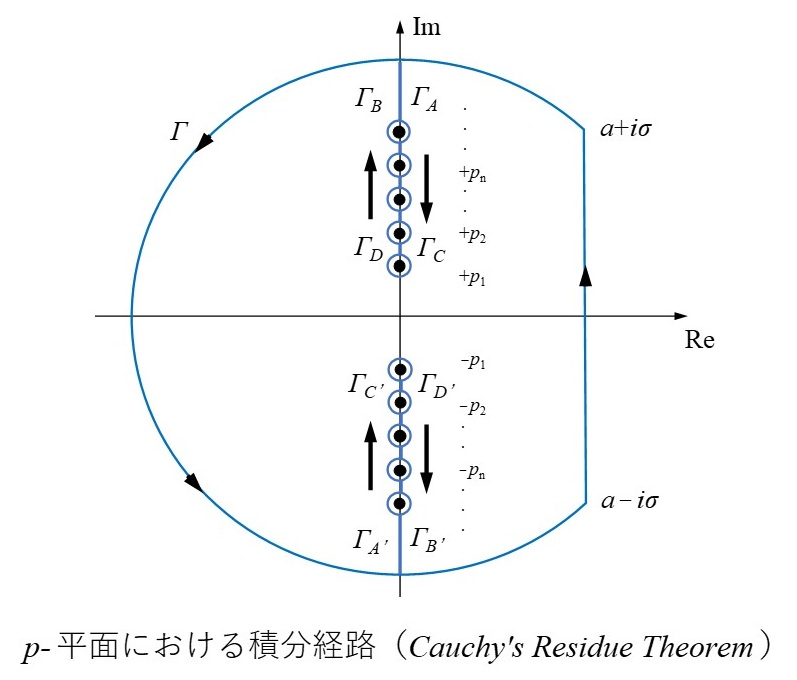
上式の積分を実行すれば、右辺第2項が消え、特異点での留数の和として解が得られる。さらに、留数値を計算する上で特異解の留数もゼロとなり、結局自由振動に関する無限個の留数の和として解が表される。これより、剛基盤を有するために固有モードが基底として働き、時間領域での解が固有モードの重ね合わせとして表現できることが理解できる。つまり、
$$\begin{Bmatrix}\tilde{u}_{1n}(ξ,z,t)\\ \tilde{u}_{2n}(ξ,z,t)\end{Bmatrix}= \sum_{i=1}^{∞}\biggl(\frac{k_{α}k_{β}V_{s}^{2}}{-|ξ|^{3}c_{i}^{3}\cdot K(p_{i})}\mathbf{A}\mathbf{E}_{sv-p}\mathbf{H}_{sv-p}\begin{Bmatrix}\tilde{Φ}_{1n}\\ \tilde{Φ}_{2n}\end{Bmatrix}T(p_{i}t)\biggr)\tag{47}$$
$$\tilde{u}_{3n}(ξ,z,t)= \sum_{i=1}^{∞}\biggl(\frac{k_{β}V_{s}^{2}}{D|ξ|c_{i}\cdot sinh(k_{β}D)}\mathbf{E}_{sh}\mathbf{H}_{sh}\tilde{Φ}_{3n}T(p_{i}t)\biggr)\tag{48}$$
ここに、\(T(p_{i}t)\) は載荷の時間関数によってそれぞれ以下のように定義される。
ディラックのデルタ関数 \(δ(t)\) に対して
$$T(p_{i}t)=2sin(|ξ|c_{i}t)\tag{49}$$
ヘヴィサイド関数の差 \(H(t)\) に対して
$$T(p_{i}t)=-\frac{2cos(|ξ|c_{i}t)}{|ξ|c_{i}}\tag{50}$$
また、\(K(p)\) は \(R_{sv-p}\) のラプラスパラメータによる1階微分より得られる関数であり、
$$K(p)=8ξ^{2}\{bg+2k_{α}^{2}k_{β}^{2}\}$$
$$-\{gq_{2}-4bk_{α}k_{β}c_{2}\}・cosh\{(k_{α}+k_{β})D\}+Dh_{1}c_{2}d_{1}・sinh\{(k_{α}+k_{β})D\}$$
$$-\{gq_{1}+4bk_{α}k_{β}c_{1}\}・cosh\{(k_{α}-k_{β})D\}+Dh_{2}c_{1}d_{2}・sinh\{(k_{α}-k_{β})D\}$$
$$ \tag{A.14}$$
ここに、
$$h_{1}=k_{α}+k_{β}(V_{s}/V_{p})^{2} ,h_{2}=k_{α}-k_{β}(V_{s}/V_{p})^{2} ,g=k_{α}^{2}+k_{β}^{2}(V_{s}/V_{p})^{2}$$
$$q_{1}=b^{2}+8ξ^{2}k_{α}k_{β}+4ξ^{4} ,q_{2}=b^{2}-8ξ^{2}k_{α}k_{β}+4ξ^{4}\tag{A.15}$$
つぎに、逆ハンケル変換を行う。逆ハンケル変換は波数に関して \(0~∞\) までの積分を実施するものであるが、離散化波数法を用いれば有限区間内 \(0≤x≤L\) で定義された波動のフーリエ級数和として解が表現される。有限区間内 \(0≤x≤L\) での離散化波数を
$$ξ_{k}=\frac{2πk}{L} (k=1,2,・・・・,K)\tag{51}$$
と定義すれば、変位解は0次(鉛直方向載荷)、1次(水平方向載荷)のフーリエ級数項に対してそれぞれ以下のように表現される。ただし、波数 \(ξ_{0}=0\) の項は消え、実際には \(k=1,2,・・・・,K\) のフーリエ級数和となる。
鉛直載荷(0次の軸対称項)に対する変位解は、
$$u_{r}(r,θ,z,t)=\frac{2π}{L} \sum_{k=1}^{K}\biggl[ \sum_{i=1}^{M}\biggl\{Φ_{12}・T(p_{i}t)・\tilde{Φ}_{20} \biggr\}・ξ_{k}・J_{1}(ξ_{k}r)\biggr]\tag{52.a}$$
$$u_{θ}(r,θ,z,t)=0\tag{52.b}$$
$$u_{z}(r,θ,z,t)=\frac{2π}{L} \sum_{k=1}^{K}\biggl[ \sum_{i=1}^{M}\biggl\{Φ_{22}・T(p_{i}t)・\tilde{Φ}_{20} \biggr\}・ξ_{k}・J_{0}(ξ_{k}r)\biggr]\tag{52.c}$$
水平載荷(1次の軸対称項,x方向載荷)に対する変位解は、
$$u_{r}(r,θ,z,t)=\frac{2π・cosθ}{L} \sum_{k=1}^{K}\biggl[ \sum_{i=1}^{M}\biggl\{Φ_{11}・T(p_{i}t)・\tilde{Φ}_{11} \biggr\}・\biggl\{\frac{J_{1}(ξ_{k}r)}{r}-ξ_{k}・J_{0}(ξ_{k}r)\biggr\}$$
$$+ \sum_{i=1}^{N}\biggl\{Φ_{33}・T(p_{i}t)・\tilde{Φ}_{31} \biggr\}・\frac{J_{1}(ξ_{k}r)}{r}\biggr]\tag{53.a}$$
$$u_{θ}(r,θ,z,t)=-\frac{2π・sinθ}{L} \sum_{k=1}^{K}\biggl[ \sum_{i=1}^{M}\biggl\{Φ_{11}・T(p_{i}t)・\tilde{Φ}_{11} \biggr\}・\frac{J_{1}(ξ_{k}r)}{r}$$
$$+ \sum_{i=1}^{N}\biggl\{Φ_{33}・T(p_{i}t)・\tilde{Φ}_{31} \biggr\}・\biggl\{\frac{J_{1}(ξ_{k}r)}{r}-ξ_{k}・J_{0}(ξ_{k}r)\biggr\}\biggr]\tag{53.b}$$
$$u_{z}(r,θ,z,t)=\frac{2π・cosθ}{L} \sum_{k=1}^{K}\biggl[ \sum_{i=1}^{M}\biggl\{Φ_{21}・T(p_{i}t)・\tilde{Φ}_{11} \biggr\}・ξ_{k}・J_{1}(ξ_{k}r)\biggr]\tag{53.c}$$
ここに、
$$\begin{bmatrix} φ_{11} & φ_{12}\\ φ_{21} & φ_{22} \end{bmatrix} \frac{k_{α}k_{β}V_{s}^{2}}{-|ξ|^{3}c_{i}^{3}\cdot K(p_{i})}\mathbf{A}\mathbf{E}_{sv-p}\mathbf{H}_{sv-p}\tag{54.a}$$
$$φ_{33}= \frac{k_{β}V_{s}^{2}}{D|ξ|c_{i}\cdot sinh(k_{β})}\tag{54.b}$$
次回は、一様成層地盤の分散特性について考察したいと思います。


コメント