時間調和波のエネルギー流束
単位面積あたりのエネルギー伝達率は、単位面積あたりの仕事率に等しく、式(16)を使用して計算できます。実数部の積は 2 つの複素数の積の実数部と同じではないため、式(16) では \(ℛ(\dot{u})\) を使用する必要があります。一次元縦応力の場合、単位面積あたりの仕事率 \(𝒫(x,t)\) は次のように得られます。
$$𝒫=ρ\enspace c_b^3\enspace k^2A^2sin^2[k(x-c_bt)]$$
$$=\frac{EA^2ω^2}{c_b}\enspace sin^2[k(x-c_bt)]\tag{84}$$
調和波の場合、単位面積あたりの仕事率は位相速度 \(c_b\) で伝わる無限の波形であることに注意してください。
単位面積あたりの時間平均仕事率
波の強度の有用な表現は、任意の位置および任意の時間における \(𝒫\) の時間平均によって表されます。この単位面積当たりの時間平均仕事率は、
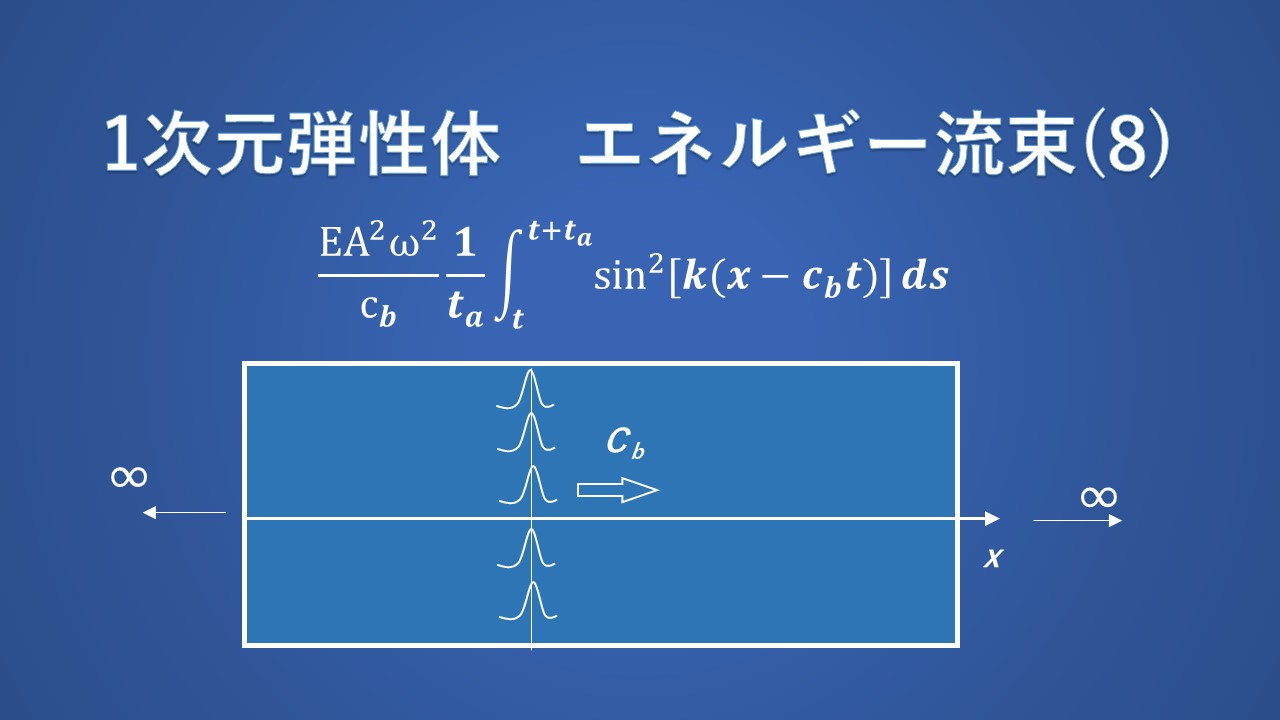
$$\frac{EA^2ω^2}{c_b}\frac{1}{t_a}\enspace \int_t^{t+t_a}sin^2(kx-ωs)ds\tag{85}$$
この積分の範囲として周期 \(t_a=T=2π/ω\) を選択すると積分部分がつぎのように評価できます。
$$\frac{1}{T}\enspace \int_t^{t+T}sin^2(kx-ωs)ds=\frac{1}{2}$$
上式を使用すると、\(<𝒫>\) で示される周期にわたる \(𝒫\) の時間平均が次のように得られます。
$$<𝒫>=\frac{1}{2}\frac{EA^2ω^2}{c_b}\tag{86}$$
CGS単位系では、\(<𝒫>\) は ergs/sec-cm2 で測定され、MKS単位系では、\(<𝒫>\) はワット/sec-m2 で表されます。\(<𝒫>\) は周波数と振幅の 2 乗に比例する特性を持ちます。
多くの場合、エネルギー計算では、2 つの複素関数 \(F\) と \(f\) の実数部の積の時間平均を評価する必要があります。ここで、\(F\) と \(f\) をつぎのように表わすと、
$$F=F_0\enspace e^{i(ωt-γ_1)}\enspace ,\enspace f=f_0\enspace e^{i(ωt-γ_2)}$$
\(F_0\) と \(f_0\) は実数部であり、つぎのような関係となります。
$$<ℛ(F)×ℛ(f)>=\frac{1}{2}ℛ(F\bar{f})\tag{87}$$
ここで、 \(\bar{f}\) は \(f\) の複素共役です。なお、式(87) は式(87) の左辺に\(F\) と \(f\) を代入することによって証明されます。また、式(87)を使用すると、\(<𝒫>\) の式(86)はすぐに得られます。
エネルギー流束の速度
平均仕事率 \(<𝒫>\) は、単位時間あたりおよび単位面積あたりの平均エネルギー伝達を表します。したがって、エネルギーの「流れ」について話すことができ、エネルギー流束の速度 \(c_e\) を導入することができます。エネルギー速度は、時間平均エネルギー伝達を総エネルギー密度の時間平均で割ったものとして定義されます。
$$<𝒫>=<ℋ>c_e\tag{88}$$
単位体積あたりの総エネルギーは、運動エネルギーとひずみエネルギーから構成されます。式(87)を使って、単位体積あたりの運動エネルギーの時間平均は次のように計算されます。
$$<𝒦>=\frac{1}{2}\frac{1}{T}\enspace \int_t^{t+T}ρ(\dot{u})^2dt=\frac{1}{4}ρA^2ω^2\tag{89}$$
同様に、ひずみエネルギー密度の時間平均は、
$$<𝒰>=\frac{1}{2}\frac{1}{T}\enspace \int_t^{t+T}E(\frac{\partial u}{\partial x})^2dt=\frac{1}{4}EA^2k^2\tag{90}$$
ここで、\(k=ω/c_b\) と \(c_b^2=E/ρ\) の関係から \(<𝒦>=<𝒰>\)。したがって、平面時間調和波の場合、時間平均エネルギー密度は、運動エネルギー密度とひずみエネルギー密度の時間平均に均等に分割されます。式(89)と式(90)の合計をとって、
$$<ℋ>=\frac{1}{2}ρA^2ω^2\tag{91}$$
式(86)と式(91)を式(88)に代入すると、速度 \(c_e\) は、
$$c_e=c_b$$
上記のことから、平面時間調和進行波におけるエネルギーの平均流量を計算するには本質的に 2 つの方法があることがわかります。一つは、トラクションと粒子速度のベクトル積の時間平均を取ることで計算されます。もう一つの方法は、単位体積あたりの運動エネルギーまたはひずみエネルギーの時間平均を計算し、いずれかの量にエネルギー伝達の速度を掛けた値を 2 倍すると、時間平均エネルギー伝達が得られます。
以上の例では、エネルギー伝達の速度は位相速度に等しくなります。これは一般に、非分散波の伝播に当てはまりますが、分散波の伝播の場合、\(c_e\) は位相速度とは異なります。
定在波のエネルギー伝達
式(81)で説明されるように、変位が反対方向に伝播する2つの波の重ね合わせからなる場合の単位面積当たりのパワーを考えてみましょう。\(u(x,t)\)の空間に関する導関数と時間に関する導関数は次のとおりです。
$$\frac{\partial u}{\partial x}=A_+kθ_++A_-kθ_-$$
$$\frac{\partial u}{\partial t}=-A_+ωθ_++A_-ωθ_-$$
ここに、
$$θ_+=exp\Bigl[i\Bigl(kx-ωt+γ_++\frac{π}{2}\Bigl)\Bigl]$$
$$θ_-=exp\Bigl[i\Bigl(kx+ωt+γ_-+\frac{π}{2}\Bigl)\Bigl]$$
\(𝒫=-τ_x\dot{u}\) の関係を使用すると、単位面積当たりの仕事率は次のように得られます。
$$𝒫=Ekω[(A_+)^2ℛ(θ_+)ℛ(θ_+)-(A_-)^2ℛ(θ_-)ℛ(θ_-)]$$
反対方向に進む波の場合、\(P\) には交差項がないため、エネルギー伝達の瞬間値でさえ個々の磁束の差にすぎないことに注意してください。式(87)を使用することにより、時間平均は次のように直ちに得られます。
$$<𝒫>=\frac{1}{2}Ekω[(A_+)^2-(A_-)^2]$$
振幅 \(A_+\) と \(A_-\) が等しい場合、エネルギーの正味の流れは存在しません。前回説明したように、このケースは定在波に対応します。実際、定在波ではエネルギーは節を越えて伝達することができず、エネルギーは節間を往復することしかできないため、どの位置でも期間 \(T\) にわたる正味の流れは消滅します。
以上、参考になれば幸いです。


コメント