今回は調和波です。ある位相を持った進行波から複素数表示を示します。その同じ周波数と波数をもつ波が逆方向に重なった場合に、ある振幅が常にゼロである固定点(節)間で振幅が上下する定在波(波の移動が見られず、sin波形の振幅が変化しているようにみえる波)と呼ばれる波。そして、ある長さの両端に境界を持たせた場合の自由振動モードを考えます。
進行波
つぎの縦方向の変位を表す式を考えてみましょう。
$$u(x,t)=Acos[k(x-ct)]\tag{74}$$
ここで、振幅 \(A\) は \(x\) と \(t\) に独立であるとします。式(74)は一般形式 \(f(x-ct)\) であるため、明らかに進行波を表します。引数 \(k(x-ct)\) は波の位相と呼ばれ、一定の位相の点は位相速度 \(c\) で伝播します。任意の \(t\) において、 \(u(x,t)\) は、波長 \(Λ(Λ=2π/k)\) をもつ \(x\) の周期関数です。 \(2π\) にわたる波長の数を表わす量 \(k=2π/Λ\) は波数と呼ばれます。どの位置でも、変位 \(u(x,t)\) は周期 \(T\) (ここで \(T=2π/ω)\) と時間調和します。角振動数 \(ω\) は次のように表されます。
$$ω=kc\tag{75}$$
したがって、\(u(x,t)\) は次のようにも表わされます。
$$u(x,t)=Acos\biggl[ω\biggl(\frac{x}{c}-t\biggr)\biggr]\tag{76}$$
式(74)と式(76)は調和進行波と呼ばれます。表現は正弦波の列を表しており、いつでも媒体の全範囲を振動します。以前に説明した過渡波(パルス)とは対照的に、調和波は定常状態の波です。
式(46)や式(71)の波動方程式に式(74)を代入すると、次のことがわかります。
$$c=c_L , c=c_b\tag{77}$$
式(77)は、一次元縦ひずみおよび一次元縦応力における調和進行波の位相速度が波長 \(Λ\) に依存しないことを示しています。これは、非常に短い波でも長い波と同じ位相速度で伝播することを意味します。位相速度が波長に依存しない場合、システムは非分散性であると言います。材料が純粋に弾性的ではなく散逸的な挙動を示す場合、調和波の位相速度は波長に依存することがわかり、そのシステムは分散性であると言われます。分散は、分散媒体中を伝播する際のパルスの形状の変化を支配するため、重要な現象です。分散は非弾性体だけでなく弾性導波路(土層や円形シリンダーなど)でも発生します。
式(76)をパラメータを変えて図化してみました。波速度による違い、位置および時間軸による進行波の様子がよくわかります。
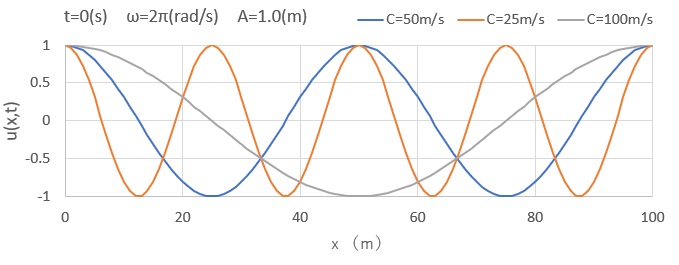
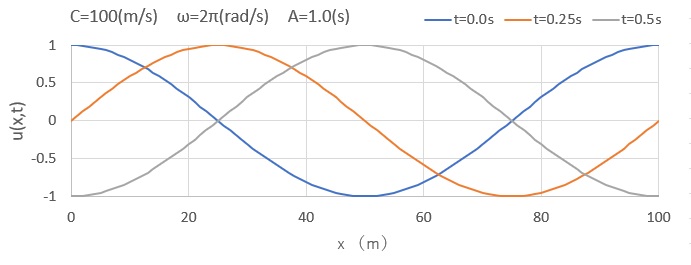

位相速度 \(c\) は、次のように得られる粒子速度 \(\dot u(x,t)\) とは明確に区別されます。
$$\dot u(x,t)=Akc・sin[k(x-ct)]$$
一次元縦ひずみの場合、粒子速度と位相速度の比の最大値は次のように得られます。
$$(\dot u/c_L)_max=Ak=2πA/Λ$$
線形理論の妥当性の範囲内では、比 \(A/Λ\) は 1 よりもはるかに小さいはずです。
複素数表示
数学的便宜のため、通常、式(74)は次のように表記します。
$$u(x,t)=A\enspace exp[ik(x-ct)]\tag{78}$$
ここで \(i=\sqrt{-1}\) 。明示的に述べることはありませんが、これ以降、式(78)の実数部または虚数部が解の物理的解釈に使用されることが理解されます。一次元の縦方向応力の場合、対応する応力は次のように表されます。
$$τ_x(x,t)=iEAk\enspace exp[ik(x-c_bt)]\tag{79}$$
そして粒子速度は次のように表わされます。
$$\dot u(x,t)=-iAkc_b\enspace exp[ik(x-c_bt)]\tag{80}$$
定在波
同じ周波数と波長を持ち、反対方向に進む 2 つの変位波を考えてみましょう。波動方程式は線形なので、結果として生じる変位は次のようになります。
$$u(x,t)=A_+e^{i(kx-ωt+γ_+)}+A_-e^{i(kx+ωt+γ_-)}\tag{81}$$
ここで、 \(A_+\) と \(A_-\) は実数値の振幅、 \(γ_+\) と \(γ_-\) は位相角です。2 つの単調波の振幅が等しい場合、 \(A_+=A_-=A\) であり、つぎのように書き換えられます。
$$u(x,t)=Ae^{i(kx+\frac{1}{2}γ_++\frac{1}{2}γ_+)}\bigl[e^{-i(ωt-\frac{1}{2}γ_++\frac{1}{2}γ_-)}+e^{i(ωt-\frac{1}{2}γ_++\frac{1}{2}γ_-)}\bigr]$$
$$ =2A\enspace exp\bigl[i(kx+\frac{1}{2}γ_++\frac{1}{2}γ_-)\bigr]cos(ωt-\frac{1}{2}γ_++\frac{1}{2}γ_-)$$
この式の実数部は次のように表せます。
$$u(x,t)=2A\enspace cos(kx+\frac{1}{2}γ_++\frac{1}{2}γ_-)\enspace cos(ωt-\frac{1}{2}γ_++\frac{1}{2}γ_-)\tag{82}$$
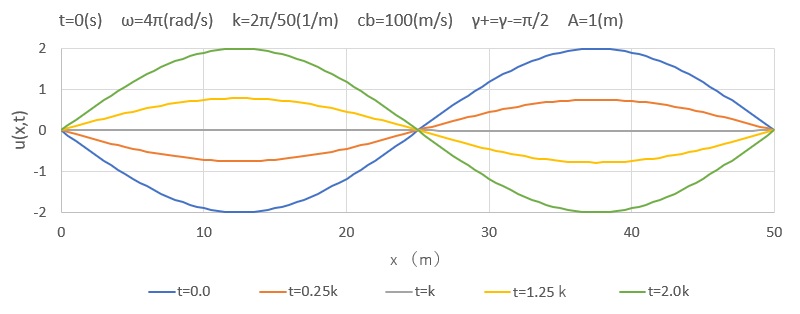
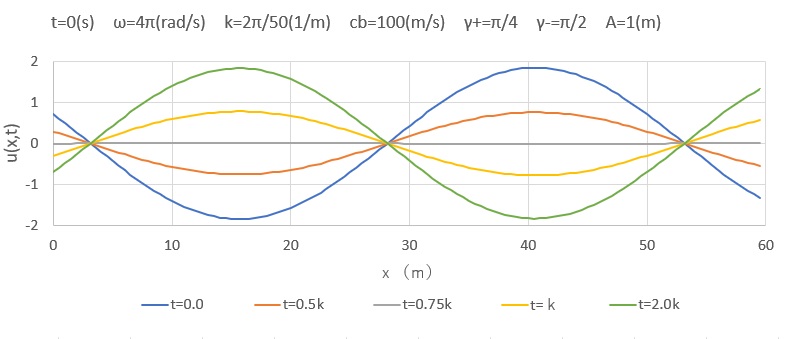
式(82)は波の形が移動しないので定在波(定常波ともいう)を表わします。\(cos(kx+\frac{1}{2}γ_++\frac{1}{2}γ_-)=0\) の点では、2 つの進行波は常に互いに打ち消し合い、媒質は静止します。これらの点は節と呼ばれます。節の各ペアの間の中間が腹であり、そこでは動きが最大の振幅になります。
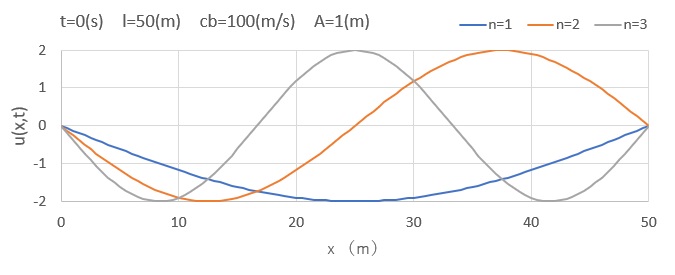
式(82)を図化してみました。左右からの進行波によって、ある位置に節が形成され、振幅のみが変化しているように見えます。
自由振動のモード
定在波は、弾性体の自由振動の特定のモードを形成します。例として棒の振動を考えます。半無限のロッドを考えて変位が \(x=0\) でゼロとなる場合、考えられる調和運動は制限を受けることになります。式(78) は使用できなくなり、節が境界 \(x=0\) と一致するように選択された角度 \(γ+\) および \(γ_-\) を持つ定在波形 式(82) を使用する必要があります。
$$γ_++γ_-=π$$
そして、
$$u(x,t)=2A\enspace sin(kx)\enspace sin(ωt-γ_+)\tag{83}$$
2 番目の境界条件として、\(x=l\) に \(u=0\) を追加すると、調和運動はさらに制限されます。今のところ、式(83) で表されるすべての調和運動のうち、\(x=l\) に節を持つものだけに制限されます。したがって、次のような条件が加えられます。
$$sin(kl)=0$$
つまり次のことを意味します。
$$kl=\frac{2πl}{Λ}=nπ n=1,\enspace 2,\enspace 3,\enspace ・・・・・$$
節と節の間の距離は波長の半分であるため、この距離は \(l,\enspace l/2,\enspace l/3\) などになる必要があります。 対応する各振動数は次のとおりです。
$$ω=kc_b=\frac{nπc_b}{l}$$
基本周波数と呼ばれる最低モードまたは基本モードの角振動数は、\(ω_0=πc_b/l\) (ラジアン/秒)であり、1秒当たりのサイクル数である基本周波数は \(f_0=c_b/2l\) です。それより高い周波数は、順次\(f_2=2c_b/2l,f_3=3c_b/2l\)のようになり、overtonesと呼ばれます。端がしっかりと支持されたロッドの例では、overtonesは基本周波数の整数倍です。基本周波数とこの単純な関係を持つovertonesは調和と呼ばれます。このセクションで説明するような単純な振動モードは、波動方程式によって支配される最も単純な振動システムに限られます。
以上、調和波について示しました。時間調和波のエネルギー流束について勉強します。



コメント