議論されている波の伝播問題の線形性の結果として、多数の別々の励起に対する全体の応答を個々の応答の重ね合わせとして表現することが許容されます。線形重ね合わせは、強制関数の積分表現と組み合わせることで、弾性波伝播の問題の解決手段を私たちに提供します。
\(x=0\) での表面力によって半空間に生成される応力波を決定するため、つぎのように応力波を定義します。
$$τ_x=-p_0\enspace e^{-ηt}\enspace H(t)\tag{101}$$
ここに、\(H(t)\) はヘビサイドの段階関数(\(H(t)=0\) (\(x<0\) のとき)、\(H(t)=1\) (\(x>0\) のとき) )です。式(97)と式(98)により、表面力はフーリエ積分にてつぎのように表わすことが出来ます。
$$τ_x(0,t)=\frac{p_0}{2πi}\int_{-∞}^{∞}\frac{e^{-ωt}}{ω+iη}dω\tag{102}$$
さて、つぎのような時間調和応力波を考えます。
$$τ_x(x,t)=\frac{1}{ω+iη}\enspace e^{-iω(t-x/c_L)}\tag{103}$$
明らかにこの波は半無限の表面力 \((ω+iη)^-1exp(-iωt)\) によって発生したものです。線形重ね合わせが許容され、積分表現式(102)の個々の成分に対する応答が式(103)で与えられるため、式(101)の形の表面力による応力は次のように表すことができます。
$$τ_x=\frac{p_0}{2πi}\int_{-∞}^{∞}e^{-iω(t-x/c_L)}\frac{dω}{ω+iη}dω\tag{104}$$
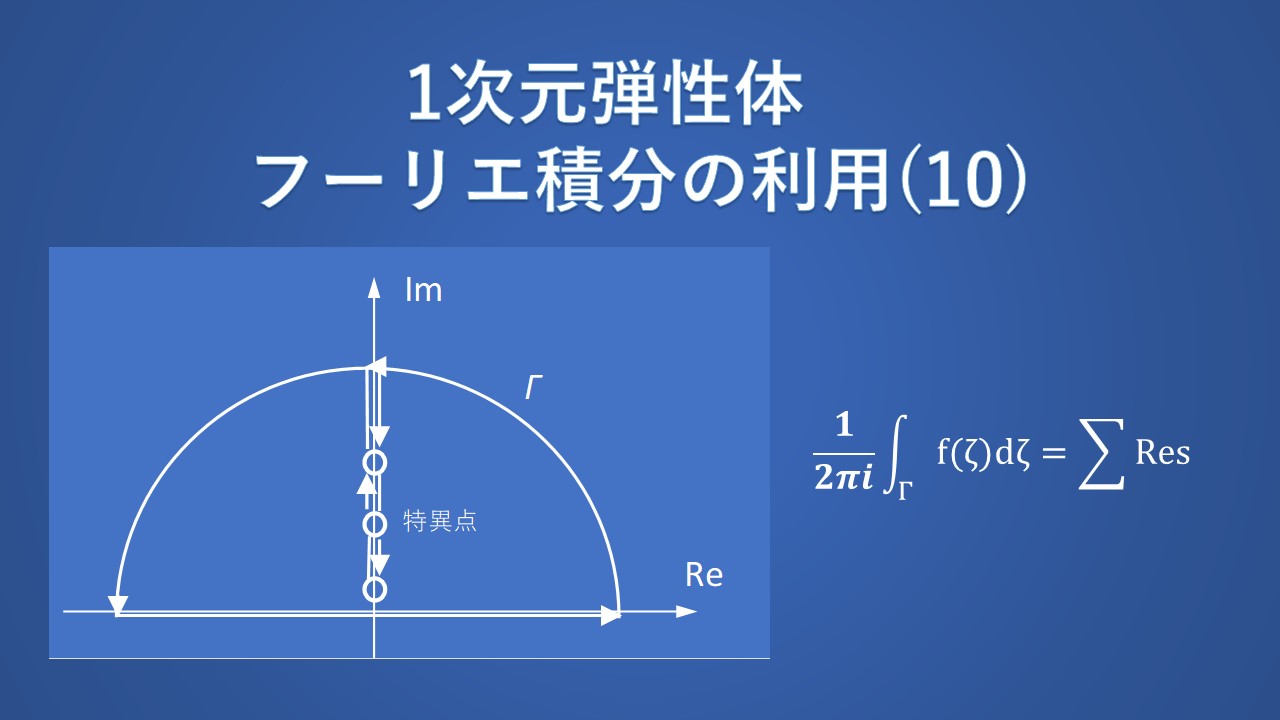
式(104)は、式(101)の形状の表面力による応力の正式な表現を提供します。式(104)の積分は、複素平面での周回積分の手法を使用して評価できます。式(104)の積分をつぎのようにおきます。
$$I=\int_{-∞}^{∞}e^{iaζ}f(ζ)dζ\tag{105}$$
ここに、\(f(ζ)\) は単一の値であり、\(a\) は実数です。これらの積分は留数定理(閉曲線に沿った周回線積分の値が閉曲線内部の孤立特異点における留数の和に \(2πi\) を掛けたものになる)によって評価され、反時計回りの積分では次のようになります。
$$\frac{1}{2πi}\int_{-∞}^{∞}e^{iaζ}f(ζ)dζ=\enspace{ } Γ内の留数の和\tag{106}$$
式(105)の積分を評価するには、実数軸と半径 \(R\) の半円からなる積分路Γを選択します。\(a>0\) のとき、半円は上平面にとられます。\(R→∞\) のとき \(F(R)→0\) (ただし、\(|f(Reiθ)|≦F(R)\) )の条件が適用される場合、\(R→∞\) とすると半円に沿った積分は消滅します。この結果はジョルダンの補題と呼ばれます。
式(104)の特定のケースでは、半円上の積分が消えるように、\(t-x/cL<0\) の場合は上半空間で積分路を閉じ、\(t-x/cL>0\) の場合は下半空間で積分路を閉じます。なお、上半平面には極がないので、次のようになります。
$$τ_x(x,t)≡0\enspace \enspace \enspace for\enspace c_L<x\tag{107}$$
下半空間には \(ω=-iη\) において極をもつため、
$$τ_x=-p_0\enspace exp\Bigl[-η\Bigl(t-\frac{x}{c_L}\Bigr)\Bigr]\enspace \enspace \enspace for\enspace c_L≧x\tag{108}$$
以上、かなり単純な例でしたが、フーリエ積分解析の機能を示しています。

コメント