今回は2つの媒体の境界における反射と透過の性質について、一次元応力波の方程式を使って考察します。やっと身近な現象が出てきてほっとしています。それでは、いきましょう。
完全反射
伝播する波動が材料特性の異なる2つの媒体間の境界面に当たると、波動の一部は反射され、一部は境界面を通過して伝達されます。第2の媒体が力学的な波を運ぶことができない特別な場合、つまり、第2の媒体が真空の場合、入射波は完全に反射されます。まず後者の場合を考えます。
さて、入射応力波が次のように表されると仮定します。
$$(τ_x)_i=f\biggl(t-\frac{x}{c_L}\biggr)\tag{66}$$
ここで、\(s<0\) の場合は \(f(s)≡0\) です。反射応力波は負の \(x\) 方向に伝播するため、次のように表すことができます。
$$(τ_x)_r=g\biggl(t+\frac{x}{c_L}\biggr)\tag{67}$$
自由境界 \(x=a\) では、応力 \(τ_x\) がゼロであるので、
$$τ_x=(τ_x)_i+(τ_x)_r=0 at x=a$$
\(t<a/c_L\) の場合、この式は \(g(t+x/c_L)≡0\) を意味し、\(t>a/c_L\) の場合、次のようになります。
$$g\biggl(t+\frac{x}{c_L}\biggr)=-f\biggl(t-\frac{x}{c_L}\biggr)$$
いま \(s=t+a/c_L\) とおくと、結局、
$$g(s)=-f\biggl(s-2\frac{a}{c_L}\biggr)$$
であり、反射応力波はつぎのように表わされます。
$$(τ_x)_r=-f\biggl(t-\frac{a}{c_L}+\frac{x-a}{c_L}\biggr)\tag{68}$$
式(68)は、反射された応力波は入射応力波と同じ形状を持つが、応力の符号は反射時に変化することを示しています。したがって、自由表面では引張応力は圧縮応力として反射され、またその逆も同様です。ただし、この場合、反射しても変位の方向は変わりません。
圧力波の引張波への変換は、引張強度が比較的低い材料に対して興味深い影響を与える可能性があります。十分に短い長さの圧縮衝撃波が自由表面で反射されると、結果として生じる引張応力が破壊を引き起こす可能性があります。急速な圧縮荷重下でのこのタイプの引張破壊は、剥離として知られる典型的な波の伝播効果です。この効果は、金属板に接触した爆薬を爆発させた B. ホプキンソンによって初めて実験的に実証されました。自由表面からの衝撃波の反射により引張破壊が生じ、これによりほぼ球形のキャップの形状をした金属のディスクが爆発薬の真反対側の表面から剥離したそうです。
インピーダンス比と反射・透過
つぎに、材料特性の異なる 2 つの媒体間の境界面での反射と透過について考えてみましょう。入射波を式(66)で表わすと、反射波と透過波はそれぞれ次のように表すことができます。
反射波:$$(τ_x)_r=g\biggl(t-\frac{a}{c_L}+\frac{x-a}{c_L}\biggr)$$
透過波:$$(τ_x)_t=h\biggl(t-\frac{a}{c_L}-\frac{x-a}{c_L^A}\biggr)$$
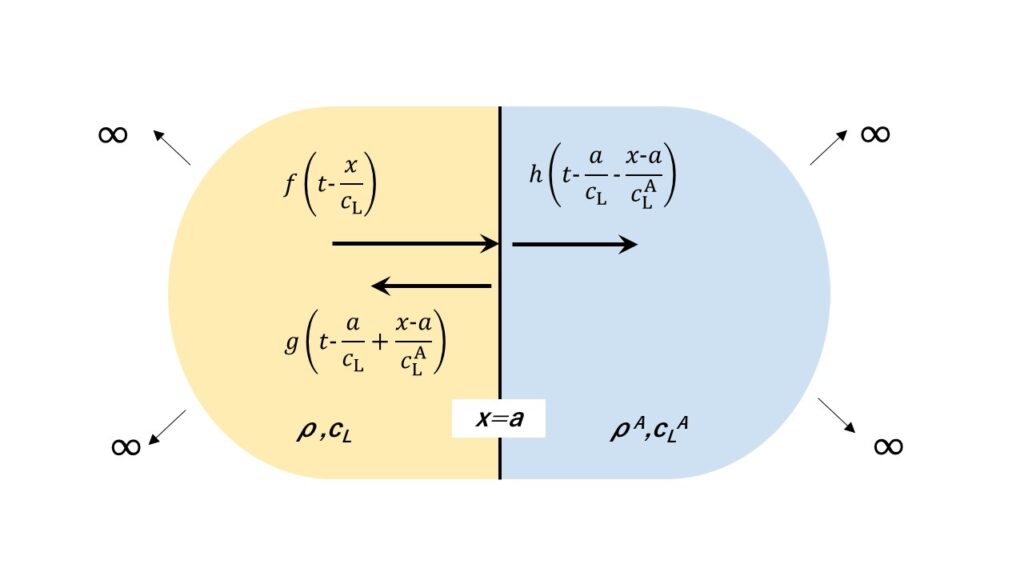
境界面 \(x=a\) における応力と粒子速度の連続性を考慮することにより、次のことがわかります。(※ \(x=a\) において、\(τ_i+τ_r=τ_t\)、\(τ=-ρc_L\dot{u}\) であり、それぞれ \(ρc_L\) で割ったものが粒子速度であるので\(τ_i/(ρc_L)-τ_r/(ρc_L)=τ_t/(ρ^Ac_L^A)\) 、これらを解くことで得られます)
$$(τ_x)_r=C_r f\biggl(t-\frac{a}{c_L}+\frac{x-a}{c_L}\biggr)$$
$$(τ_x)_t=C_t f\biggl(t-\frac{a}{c_L}-\frac{x-a}{c_L^A}\biggr)$$
反射係数 \(C_r\) と透過係数 \(C_t\) は
$$C_r=\frac{ρ^Ac_L^A/ρc_L-1}{ρ^Ac_L^A/ρc_L+1}$$
$$C_t=\frac{2ρ^Ac_L^A/ρc_L}{ρ^Ac_L^A/ρc_L+1}$$
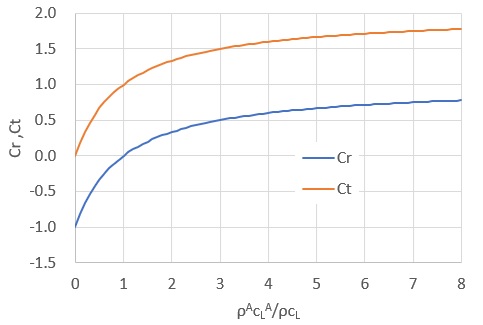
これらの式は、材料のインピーダンス比が境界面での反射と透過の性質を決定することを示しています。図では、反射係数と透過係数が力学的インピーダンス比に対してプロットされています。 \(ρ^Ac_L^A/ρc_L=0\) は自由境界であり、式(68)の結果 \(C_r=-1\) 、\(C_t=0\) となります。\(ρ^Ac_L^A/ρc_L=1\) のときは完全に透過する。\(r>1\) の場合は、反射波は入射波と同じ符号となり、透過波は常に入射波と同じタイプです。
多数の層が続いている場合でも、その過渡波のパターンを 1 次元幾何学で解くことができます。反射と透過の連続により、圧縮荷重下での高い引張応力など、予期せぬ影響が生じる場合もあります。それはAchenbachらによって解析と実験によって示され、セグメント化されたロッドの端に隣接する最初の境界面で、短時間の圧縮荷重がかかると引張破壊が発生する可能性があります。力学的インピーダンスが大きく異なるセグメントがあると、特に最初のセグメントの力学的インピーダンスが比較的小さい場合、障害が発生します。
次回は、一次元縦応力波です。進行方向の直角方向にひずみが発生する条件と応力が発生する条件の違いによって、対象物が異なることを考察します。


コメント