今回は、前回までに示した一様成層地盤の波動の特性方程式の根をExcel VBA(2021)を使って求め、波の伝播速度として位相速度および群速度を定義し、振動数との関係曲線(分散曲線)を描いています。これから、一様成層地盤の波動の分散特性について考察を行いました。
分散曲線とは
半無限地盤内の波動は、実体波のP波およびS波と表面波のRayleigh波よりなり、これらの波の伝播速度は地盤物性から一意的に決定されます。Rayleigh波は自由表面での境界条件によって発生するのであり、振幅が自由表面からの深さとともに急激に小さくなる波、すなわちエネルギーが自由表面付近に集中してくる波で、表面に沿って伝播します。そして、その伝播特性はポアソン比と強い相関を持ちます。
これに対して、成層地盤内の波の伝播速度は振動数(波数)によって変化します。それ故、異なる速度を持つ波が伝播するために波動はより複雑となり、いわゆる波動の分散現象が現れます。当該対象モデルでの振動数(波数)と波の伝播速度の関係は、面内波動場および面外波動場に対する波動の特性方程式(式(37)、式(38))の根より求められます。波の伝播速度として位相速度あるいは群速度を定式化し、振動数(波数)との関係を描いた曲線は分散曲線と呼ばれ、これにより波動の伝播特性を大まかに知ることができます。位相速度は各波の伝播速度を表わし、振動数 \(f\) と波数 \(ξ\) によって \(V=2πf/ξ\) と定義されます。一方、群速度は \(V_{g}=2π(df/dξ)\) で定義され、見かけの伝播速度を表わします。分散曲線での勾配が急なところは波動の分散が著しく振幅が小さくなり、穏やかなところでは大きな振幅となります。特に、群速度が極小となる波は他の周波成分よりも顕著に表れ、この相はAiry相と呼ばれます。
以下では、分散曲線から一様成層地盤の分散特性について考察します。
特性方程式の根の計算
Excel VBAでは波数 \(ξ\) を変数として設定し、ある \(ξ\) に対して振動数 \(f\) を変数として特性方程式がゼロとなる値を探しています。面内波動の特性方程式の根を求める際には、Excel VBAでは複素数の扱いが充実していないため、 \(V_{s}/(2π)<f<V_{p}/(2π)\) のときは特性方程式が虚数、その他の範囲では実数という条件の下で計算を行いました。
一方、面外方程式は、\(cosh(k_{β}D)\) がゼロとなる波数 \(ξ\) と振動数 \(f\) の組み合わせを見つければよいので、ある \(ξ\) に対して \(f=V_{s}/(2π)(ξ^{2}+(π/(2D))^{2}・(2n+1)^{2})^{1/2},n=0,1,2,・・・\) として求められます。
また、Excel VBAでは波数 \(ξ\) が大きくなると発散するため、計算には限界があり、\(ξD<400\) の範囲で特性方程式の根を計算しています。
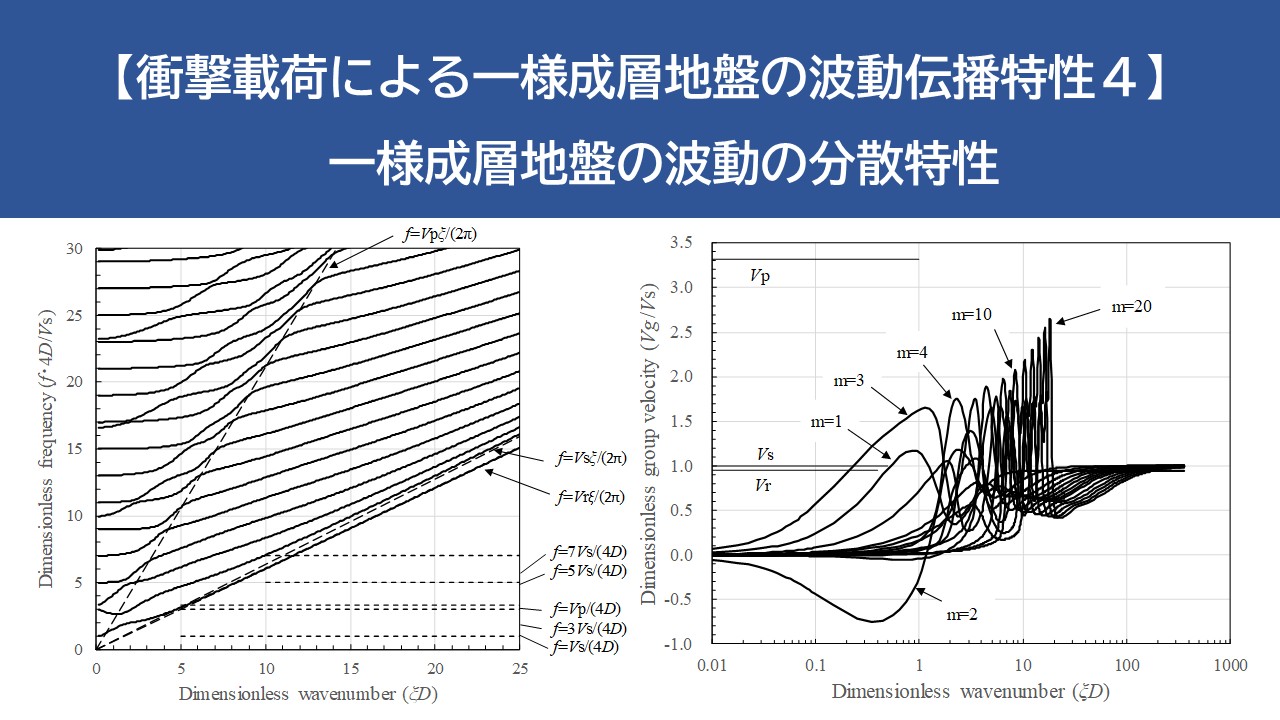
面内波動場の分散特性
面内波動場における分散曲線として、計算上の層厚を10m、 \(V_{s}=200m/s\) とし、地盤のポアソン比を \(ν=0.30\) と \(ν=0.45\) とした場合の結果を示します。各モード次数は振動数の小さいものから順に1次、2次と定義し、図中には m=1,2,・・・ と表示します。
まず、位相速度の分散曲線では、波数が大きくなる(層厚に比して波長が短くなる)と、1次モードはポアソン比に対応した半無限地盤でのRayleigh波速度 \(V_{r}\) に漸近し、2次モード以降は \(V_{s}\) に漸近しています。そして、波数が小さくなる(層厚に比して波長が長くなる)に従って位相速度は増加し、一旦 \(V_{p}\) に漸近したのち急激に増加しています。\(V_{p}\) への漸近の様子はポアソン比によって異なり、\(ν=0.30\) の場合には低次モードから同現象が明確に現れているのに対し、 \(ν=0.45\) の場合には20次程度の高次モードにおいて同現象が現れます。また、波数が小さくなる(層厚に比して波長が長くなる)領域では、位相速度が急激に増加しており実現象では見られない \(V_{p}\) 以上の速度を持ちます。これは同領域が地盤振動を形成する領域であることを意味します。
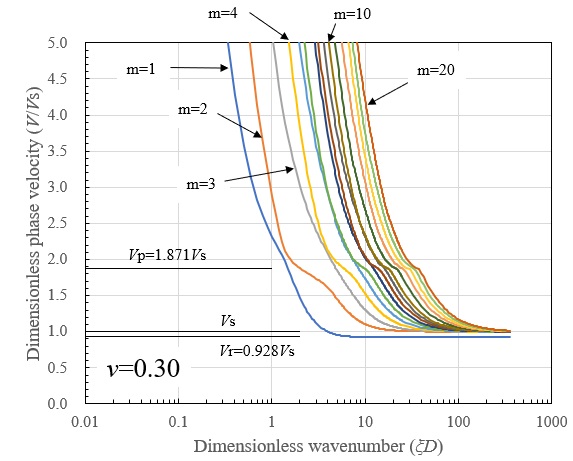
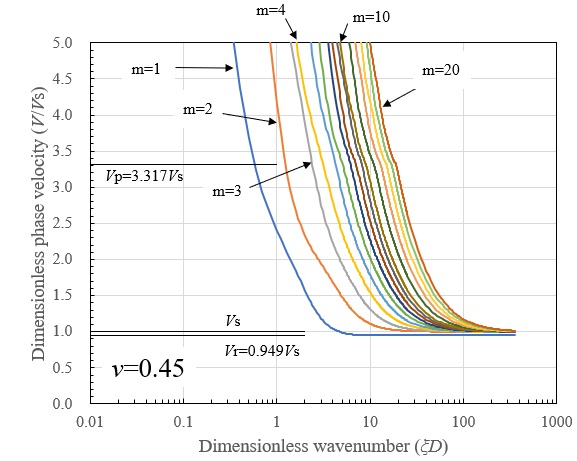
つぎに、群速度の分散曲線を示します。波数が大きくなる(層厚に比して波長が短くなる)と、位相速度と同様に1次モードはそれぞれのポアソン比に対応した半無限地盤でのRayleigh波速度 \(V_{r}\) に漸近し、2次モード以降は \(V_{s}\) に漸近しています。従って、この領域では半無限地盤での条件に近づき、S波およびRayleigh波の直達波を形成するものと考えられます。また、各モードの位相速度が \(V_{p}\) に漸近する波数において、対応するモードの群速度が \(V_{p}\) 近傍の値を示しています。P波による直達波はこの領域で形成されるものと考えられますが、高いポアソン比を持つ地盤ではP波の直達波が顕著に現れにくいことが予想されます。さらに、同波数領域よりも波数が小さくなると、各モードのAiry相を含んだ複雑な分散性が現れますが、 \(V_{p}\) 以上の群速度は現れず、実現象と一致します。位相速度が \(V_{p}\) 以上の速度となっている波数(層厚に比して波長が長い)領域での群速度は0に漸近しており、波数が層厚に比べて非常に長くなると波の伝播が起こらないことが分ります。
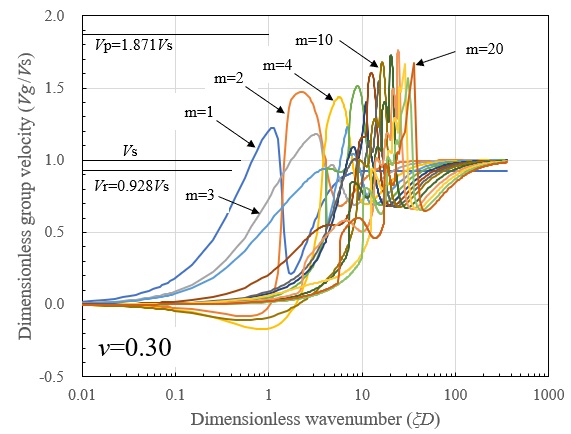
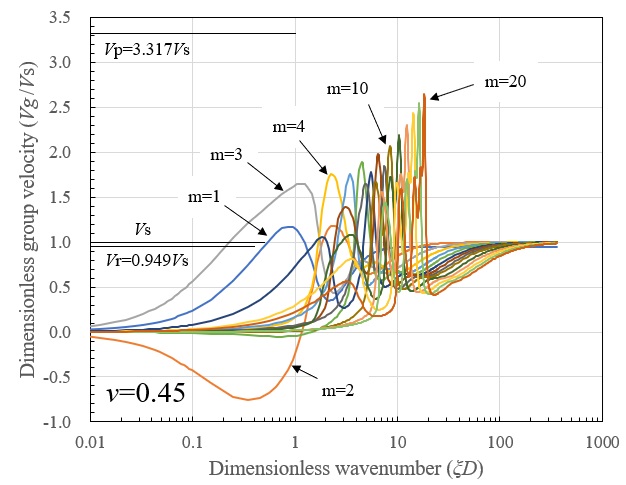
以下に示す振動数の分散曲線には位相速度が \(V_{r}\) , \(V_{s}\) , \(V_{p}\) に一致する位置を、それぞれ点線で \(f=V_{r}ξ/2π\) , \(f=V_{s}ξ/2π\) , \(f=V_{p}ξ/2π\) として示していますが、同図からも上述の波数の分散特性が確認されます。さらに波数が小さくなると、振動数が地盤の固有振動数 \(f=nV_{s}/4D\) , \(f=nV_{p}/4D(n=1,2,3,・・・)\) に漸近しており、同領域が地盤振動を形成する領域であることが確認されます。そして、1次モード以下の振動数領域では波数および振動の存在しない領域があり、剛基盤上の層状地盤では遮断振動数が存在することが分ります。
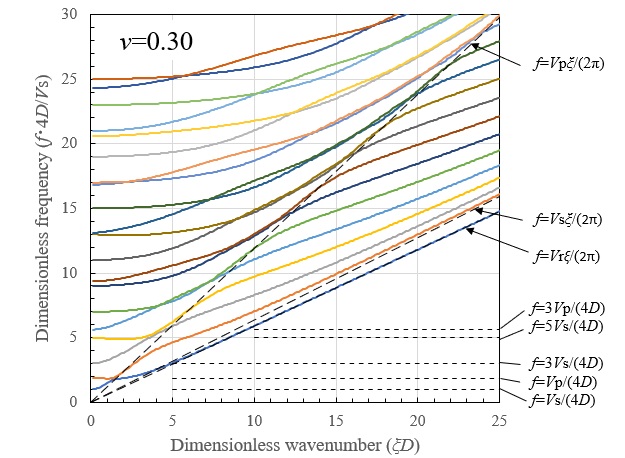
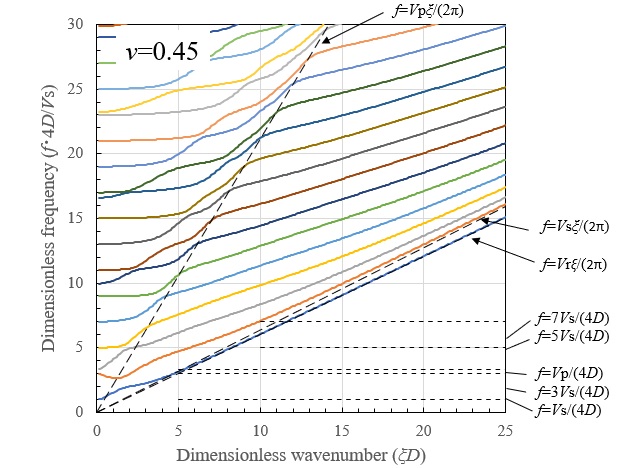
以上より、波数の小さな領域では定常振動を、波数の大きな領域では直達波を、それらの中間の波数領域では各モードのAiry相を含む遷移波動を形成し、成層地盤の遷移応答はこれらが複合されたものと言えます。ただし、これらの波数領域は層厚によって変化することに注意しなければなりません。つまり、同じ波数成分よりなる波動でも、層厚が薄くなれば \(ξD\) が小さくなり地盤振動が卓越するのに対して、層厚が厚くなれば \(ξD\) が大きくなり半無限地盤と同じように直達波が卓越します。
面外波動場の分散特性
面外波動場における分散曲線を以下に示します。
位相速度の分散曲線では、波数が大きくなる(層厚に比して波長が短くなる)と、各モードは \(V_{s}\) に漸近しています。そして、波数が小さくなる(層厚に比して波長が長くなる)に従って位相速度は増加しています。
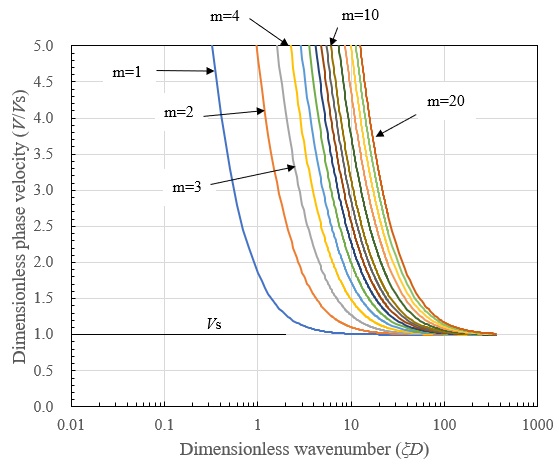
群速度の分散曲線では、波数が大きくなる(層厚に比して波長が短くなる)と位相速度と同様に各モードは \(V_{s}\) に漸近しており、S波の直達波を形成するものと考えられます。また、 \(V_{s}\) 以上の群速度は現れず、位相速度が \(V_{s}\) 以上の速度となっている波数(層厚に比して波長が長くなる)領域での群速度は0に漸近しており、波長が層厚に比して非常に長くなると波の伝播が起こらないことが分ります。
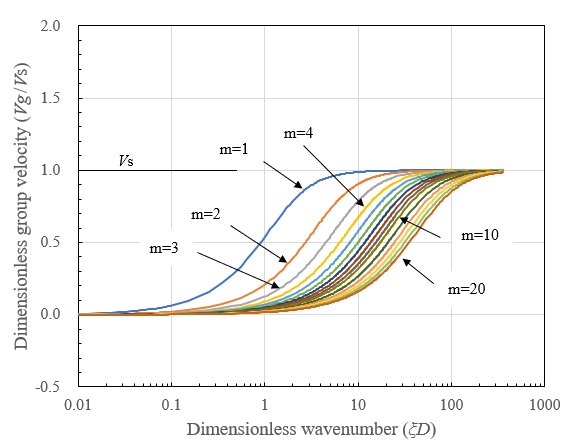
振動数の分散曲線には位相速度が \(V_{s}\) に一致する位置を、それぞれ点線で \(f=V_{s}ξ/2π\) として示しています。同図からも上述の波数の分散特性が確認され、波数が小さくなると振動数が地盤の固有振動数 \(f=nV_{s}/4D(n=1,2,3,・・・)\) に漸近しており、同領域が地盤振動を形成する領域であることが確認されます。そして、1次モード以下の振動数領域では波数および振動の存在しない領域があり、剛基盤上の層状地盤では遮断振動数が存在することが分ります。
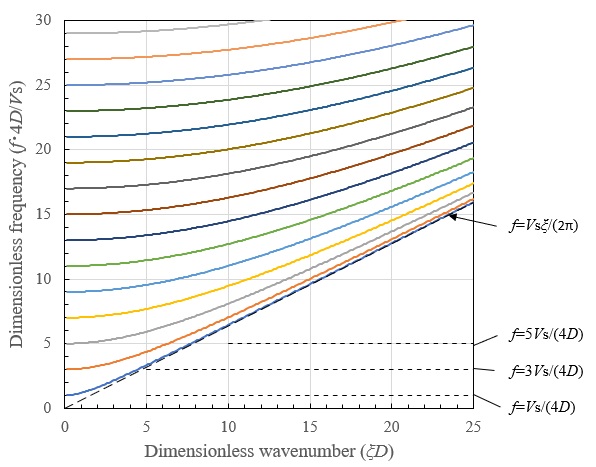
以上のように、一様成層地盤での面外波動場では、2層半無限地盤に現れるLave波モードのようなAiry相を持たず、SH波しか存在しないために、面内波動場でのような複雑な分散曲線とはなりません。しかし、波動の分散性は各振動領域で面内波動と同様な傾向を示しています。
さて、次回は各モードの伝達関数や応答値を示したいと思いますが、まずはVBAで何処まで出来るかやってみたいと思います。


コメント