地震応答スペクトル計算(1)に示した1自由度系の運動方程式を振動数領域で計算し、地震応答スペクトルを求めてみます。ExcelはOffice2021を用いました。時刻歴解析についても説明していますのでご興味のある方は、ExcelVBAで地震応答スペクトル計算(2)中央差分法で運動方程式を解くまたはExcelVBAで地震応答スペクトル計算(3)線形加速度法で運動方程式を解くをご覧ください。
振動数領域解の定式化
時間\(t\) における1自由度系の運動方程式は、つぎのように表せます。
$$\ddot{u}(t)+2hω_0・\dot{u}(t)+ω_0^2・u(t)=-\ddot{u}_G(t)\tag{1}$$
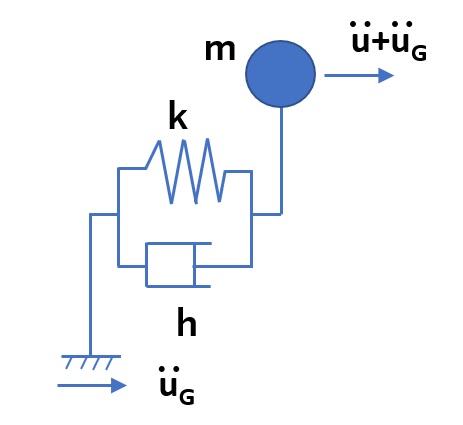
ここで、\(ω_0\) は構造物の固有角振動数、\(h\) は減衰比です。
さて、式(1)を振動数領域に変換します。変位、地震入力加速度に、つぎのフーリエ逆変換の関係を代入すると、運動方程式は式(4)のように表されます。
$$u(t)=\frac{1}{2π}\int_{-∞}^∞U(ω)e^{-iωt}dω\tag{2}$$
$$\ddot{u}_G(t)=\frac{1}{2π}\int_{-∞}^∞A_g(ω)e^{-iωt}dω\tag{3}$$
$$(-ω^2+2ihω・ω_0+ω_0^2)\frac{1}{2π}\int_{-∞}^∞U(ω)e^{-iωt}dω=-\frac{1}{2π}\int_{-∞}^∞A_g(ω)e^{-iωt}dω\tag{4}$$
したがって、変位の振動数領域解を次式で求めて、これをフーリエ逆変換すれば、時間領域の変位が求まります。速度、加速度は、それぞれ変位の振動数成分に \(iω\) 、\(-ω^2\) を乗じてフーリエ逆変換を実行すれば得られます。
$$U(ω)=\frac{A_g(ω)}{ω^2-2ihω・ω_0-ω_0^2}\tag{5}$$
$$\dot{u}(t)=\frac{1}{2π}\int_{-∞}^∞iωU(ω)e^{-iωt}dω\tag{6}$$
$$\ddot{u}(t)=\frac{1}{2π}\int_{-∞}^∞-ω^2U(ω)e^{-iωt}dω\tag{7}$$
ここに、式(5)の \(1/(ω^2-2ihω・ω_0-ω_0^2)\) は伝達関数とよばれ、各振動数の応答倍率を表します。下図は、構造物の固有振動数0.5sと1.0s、減衰定数0.5の場合の伝達関数の絶対値を示したものですが、各固有周期が卓越するような関数となります。
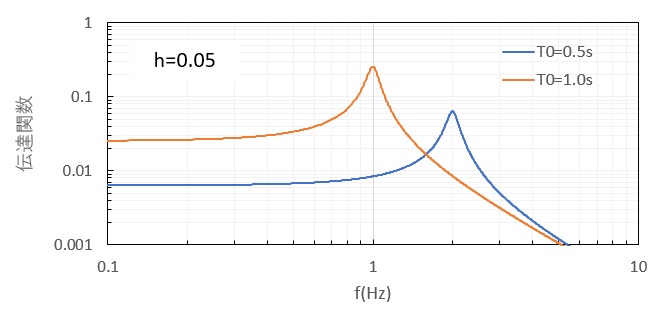
時刻歴解析の場合は、時間ステップ毎に直接時刻歴応答を求めていきましたが、振動数領域での解法では伝達関数と地震波の振動数成分との合積をとることで、各固有周期毎の時刻歴応答を求めていきます。両解法ともに、得られた時刻歴応答に対して、それぞれの応答の最大値を抽出して応答スペクトルを求めていきます。
メインプログラム
メインプログラムでは、
- 入力データの読み取り
- 地震波のフーリエ変換(FFT)
- 固有周期毎に応答最大を計算 → 応答スペクトル作成
の指示を行っています。なお、今回は複素フーリエを用いていますので、複素数の計算をFUNCTIONで定義しています。この複素数計算のFUNCTIONや高速フーリエ変換FFTについてはExcelVBAで高速フーリエ変換FFTを作成してみたに、それぞれ示していますので参考にしてください。
Option Explicit
'********************************************************
' ND :地震波のデータ数 , DT :地震波のΔt
' N :フーリエデータ数
' AG() :地震波入力加速度 , OMG :固有角振動数
' T0() :固有周期(s) , NT0 :固有周期の分割数
' h :減衰比 , Fk() :振動数→角振動数
' ACC() :加速度応答 , VEL() :速度応答
' DSP() :変位応答
' ACCmax:加速度の最大値 , VELmax:速度の最大値
' DSPmax:変位の最大値
' UX() :変位の複素数(FFT) , VX() :速度の複素数(FFT)
' AX() :加速度の複素数(FFT) , FAG() :AGの複素数(FFT)
'********************************************************
Dim ND, N, NT0 As Long
Dim AG(16384), DT, OMG, T0(101), h, Fk(8193) As Double
Dim ACC(16384), VEL(16384), DSP(16384) As Double
Dim ACCmax, VELmax, DSPmax As Double
Dim i, iT, J, K, M, Kmax, Istep, IND As Long
Dim pi As Double
Dim UX(16384) As complex
Dim VX(16384) As complex
Dim AX(16384) As complex
Dim FAG(16384) As complex
'=== 複素数と複素行列の型 ===
Type complex
re As Double '実部
im As Double '虚部
End Type
Sub メインプログラム()
pi = 3.14159265359
Worksheets("Input").Activate
Call 入力データ(FAG)
Worksheets("AmpSpec").Activate
Call フーリエ変換(FAG)
Worksheets("応答スペクトル").Activate
For iT = 1 To NT0 + 1
OMG = 2# * pi / T0(iT)
Call 応答スペクトル(iT)
Next iT
End Sub
入力データ
入力データは、sheet”Input”に記入してある各パラメータと地震波時刻歴を読み取り、つぎのFFTのために地震波を複素数に入れ替えています。
'=== 計算条件、地震加速度の読み込み ====================
Sub 入力データ(x() As complex)
Dim DT0 As Double
ND = Range("E2").Value
DT = Range("E3").Value
T0(1) = Range("E4")
NT0 = Range("E6")
T0(NT0 + 1) = Range("E5")
h = Range("E7")
DT0 = (Log10(T0(NT0 + 1)) - Log10(T0(1))) / NT0
For i = 2 To NT0
T0(i) = 10 ^ (Log10(T0(i - 1)) + DT0)
Next i
For i = 1 To 14
Kmax = 2 ^ i
If ND <= Kmax Then
N = Kmax
Exit For
End If
Next i
If ND > Kmax Then
MsgBox "データ数>16384 計算を終了します。", vbOKOnly
End
End If
For i = 1 To ND
AG(i) = Cells(i + 1, 8)
x(i) = cn(Cells(i + 1, 8), 0#)
Next i
If N > ND Then
For i = ND + 1 To N
AG(i) = 0#
x(i) = cn(0#, 0#)
Next i
End If
End Sub
今回の計算データは、sheet”Input”内に以下のように収容しています。
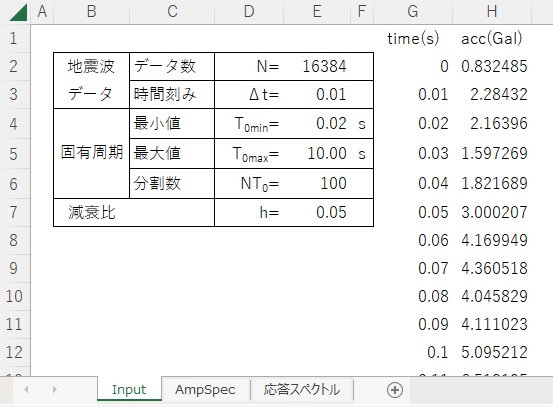
地震加速度のフーリエ変換
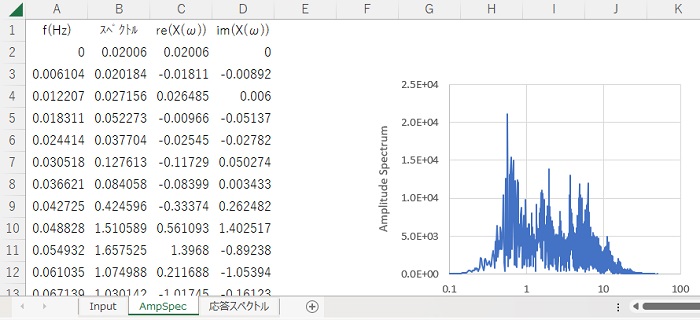
地震加速度のフーリエ変換後、sheet”AmpSpec”に振動数成分を出力しています。
'=== 地震加速度のフーリエ変換 ==========================
Sub フーリエ変換(x() As complex)
Call fast(x, -1)
For i = 1 To N / 2 + 1
Fk(i) = (i - 1) / N / DT
Cells(i + 1, 1) = Fk(i)
Cells(i + 1, 2) = cabs(x(i))
Cells(i + 1, 3) = x(i).re
Cells(i + 1, 4) = x(i).im
Fk(i) = 2# * pi * Fk(i)
Next i
End Sub
応答スペクトルの計算
”応答スペクトル()”にて1つの固有周期に対する時刻歴変位、時刻歴速度、時刻歴加速度の最大応答値を求め、sheet”応答スペクトル”に出力していきます。まず、
- 構造物の固有周期から伝達関数を求め、
- 地震波の振動数成分から変位、速度、加速度の振動数領域解を求めます。
- その結果を高速フーリエ逆変換して時刻歴解を求め、
- 各応答値の絶対値の最大を求めて、
- sheet”応答スペクトル”に出力します。
'=== 応答スペクトルの計算 ==============================
Sub 応答スペクトル(iT)
Dim O2, hO As Double
Dim C As complex
O2 = OMG * OMG
hO = 2# * h * OMG
'------- fk=0.0Hzの計算 ------------------------------
C = cn(-O2, 0#)
UX(1) = cbar(FAG(1), C)
VX(1) = cn(0#, 0#)
AX(1) = cn(0#, 0#)
'------- fk=1/(NΔt)~(N-2)/(2NΔt)Hzの計算 ---------
For i = 2 To N / 2
C = cn(Fk(i) ^ 2 - O2, -hO * Fk(i))
UX(i) = cbar(FAG(i), C)
C = cn(0#, Fk(i))
VX(i) = cpro(UX(i), C)
C = cn(-Fk(i) ^ 2, 0#)
AX(i) = cpro(UX(i), C)
'----- N/2+2~Nへの共役複素数の折り返し ----------
UX(N - i + 2) = cjg(UX(i))
VX(N - i + 2) = cjg(VX(i))
AX(N - i + 2) = cjg(AX(i))
Next i
'------- fk=1/(2Δt)Hzの計算 -------------------------
i = N / 2 + 1
C = cn(Fk(i) ^ 2 - O2, -hO * Fk(i))
UX(i) = cbar(FAG(i), C)
C = cn(0#, Fk(i))
VX(i) = cpro(UX(i), C)
C = cn(-Fk(i) ^ 2, 0#)
AX(i) = cpro(UX(i), C)
'------- 逆フーリエ変換 -------------------------------
Call fast(UX, 1)
Call fast(VX, 1)
Call fast(AX, 1)
'------- 最大応答値の抽出 -----------------------------
ACCmax = 0#
VELmax = 0#
DSPmax = 0#
For i = 1 To N
DSP(i) = UX(i).re / N
VEL(i) = VX(i).re / N
ACC(i) = AX(i).re / N + AG(i)
If DSPmax < Abs(DSP(i)) Then
DSPmax = Abs(DSP(i))
End If
If VELmax < Abs(VEL(i)) Then
VELmax = Abs(VEL(i))
End If
If ACCmax < Abs(ACC(i)) Then
ACCmax = Abs(ACC(i))
End If
Next i
'------- sheetへの出力 ---------------------------------
Cells(iT + 1, 1).Value = T0(iT)
Cells(iT + 1, 2).Value = ACCmax
Cells(iT + 1, 3).Value = VELmax
Cells(iT + 1, 4).Value = DSPmax
End Sub
下図は計算結果が出力されたsheetの状況です。
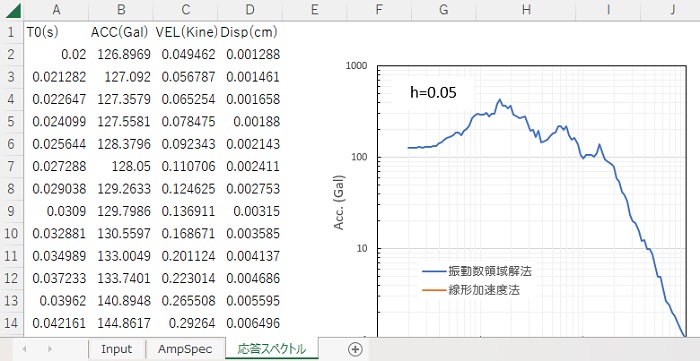
振動数領域計算の精度
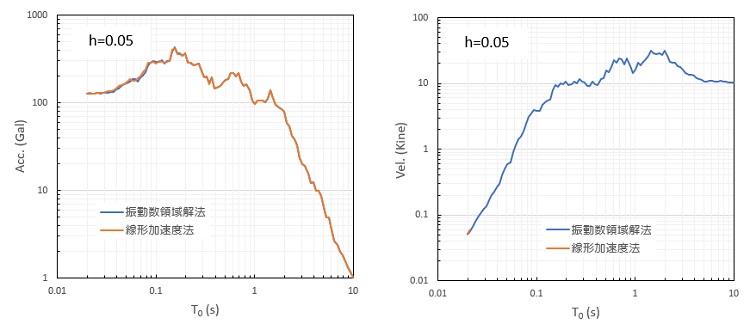
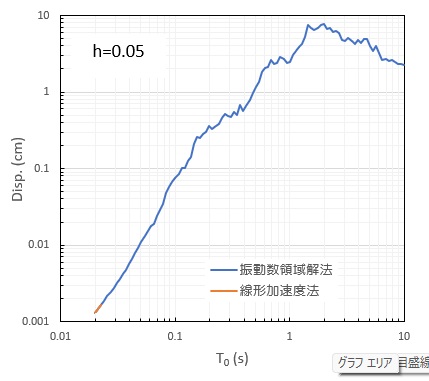
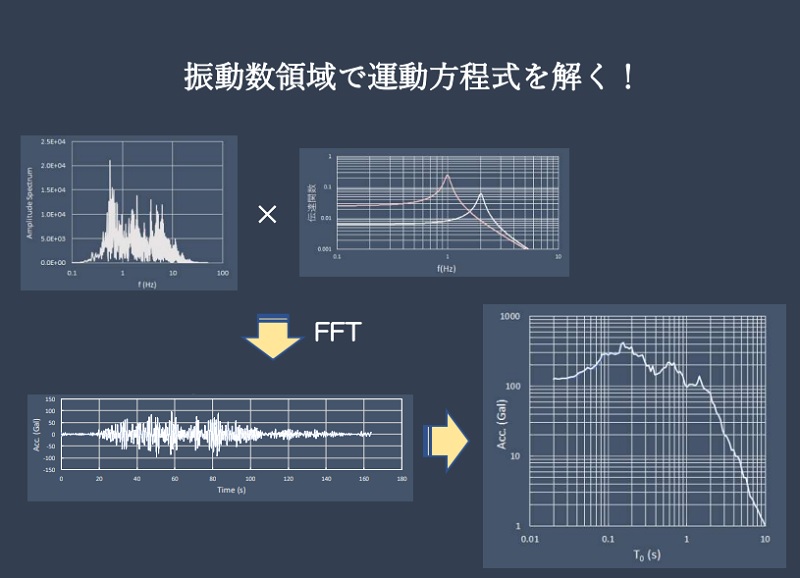
固有周期1.0s、減衰定数0.05の応答時刻歴を、線形加速度法と比較して示しますが、ほとんど変わりない結果となっているのが分かります。
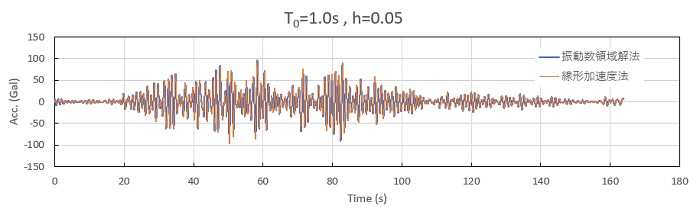
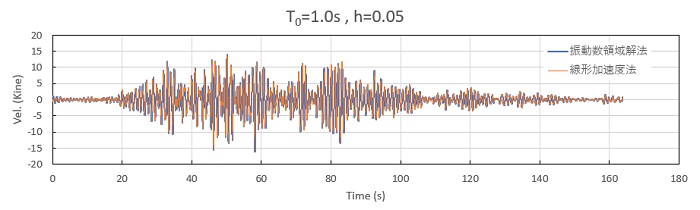
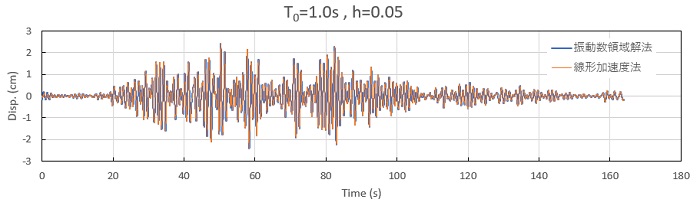
つぎに応答スペクトルを線形加速度法と比較したものですが、加速度、速度、変位は両結果がほぼ完全に重なっています。したがって、振動数領域解も時刻歴領域解も、ExcelVBAで十分な精度の解が計算できることが分かります。






コメント