今回のシリーズでは、剛基盤上の一様成層地盤の波動伝播特性について、勉強していきます。まずは、ラプラス・波数領域の一般解を導きます。その際、周方向にフーリエ級数展開し、半径方向にはハンケル変換を行います。
フーリエ・ベッセル変換対
3次元一様弾性体の波動方程式(Naviorの式)は一般的につぎのように表わされます。
$$μ\mathbf{∇}^2\mathbf{u}+(λ+μ)\mathbf{∇∇}・\mathbf{u}+\mathbf{f}=ρ\ddot{\mathbf{u}}\tag{1}$$
ここに、\(\mathbf{u}\) は変位ベクトル、\(\mathbf{f}\) は物体力ベクトル、\(ρ\) は単位体積重量、\(λ\) および \(μ\) はラーメ定数、\(\ddot{\mathbf{u}}\) は変位の時間に関する2階微分をそれぞれ表わします。
上式に時間に関するラプラス変換を行い、ラプラス領域での支配方程式を導いていきます。ラプラス変換対は、
$$\bar{u}(p)=\int_{0}^{∞}u(t)・e^{-pt}dt\tag{2}$$
$$u(t)=\frac{1}{2πi}\int_{α-i∞}^{α+i∞}\bar{u}(p)・e^{pt}dp\tag{3}$$
と定義され、\(t\) は時間、\(p\) はラプラスパラメータを表わし、\(\bar{u}\) はラプラス領域量であることを示します。式(1)に式(2)の変換を実施して、さらに下図の左手系円筒座標系での支配方程式として表わせば、
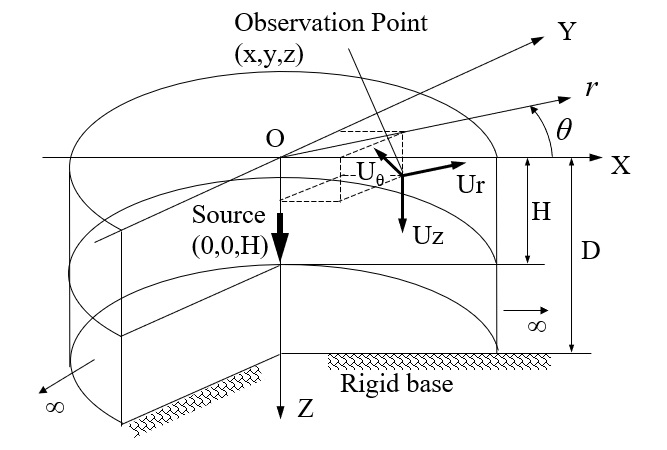
$$(λ+2μ)\frac{\partial \bar{\mathbf{\Delta}}}{\partial r}-\frac{2μ}{r}\frac{\partial \bar{\mathbf{Ω}}_z}{\partial θ}+2μ\frac{\partial \bar{\mathbf{Ω}}_θ}{\partial z}-ρp^2\bar{u}_r+\bar{f}_r=0\tag{4.a}$$
$$(λ+2μ)\frac{1}{r}\frac{\partial \bar{\mathbf{\Delta}}}{\partial θ}-2μ\frac{\partial \bar{\mathbf{Ω}}_r}{\partial z}+2μ\frac{\partial \bar{\mathbf{Ω}}_z}{\partial r}-ρp^2\bar{u}_θ+\bar{f}_θ=0\tag{4.b}$$
$$(λ+2μ)\frac{\partial \bar{\mathbf{\Delta}}}{\partial z}-\frac{2μ}{r}\frac{\partial }{\partial r}(r\bar{\mathbf{Ω}}_θ)+\frac{2μ}{r}\frac{\partial \bar{\mathbf{Ω}}_r}{\partial θ}-ρp^2\bar{u}_z+\bar{f}_z=0\tag{4.c}$$
ここで、\(u\) は変位、\(f\) は物体力を表わします。添字\(r\)、\(θ\)、\(z\)は円筒座標における半径方向、周方向、深さ方向を示します。また、\(\bar{\Delta}\)は体積膨張率、\(\bar{\mathbf{Ω}}\)は以下のようです。
$$\bar{\mathbf{\Delta}}=\frac{1}{r}\frac{\partial }{\partial r}(r\bar{u}_r)+\frac{1}{r}\frac{\partial \bar{u}_θ}{\partial θ}+\frac{\partial \bar{u}_z}{\partial z}\tag{5}$$
$$\bar{\mathbf{Ω}}_r=\frac{1}{2}\Bigl(\frac{1}{r}\frac{\partial \bar{u}_z}{\partial θ}-\frac{\partial \bar{u}_θ}{\partial z}\Bigr)\tag{6.a}$$
$$\bar{\mathbf{Ω}}_θ=\frac{1}{2}\Bigl(\frac{\partial \bar{u}_r}{\partial z}-\frac{\partial \bar{u}_z}{\partial r}\Bigr)\tag{6.b}$$
$$\bar{\mathbf{Ω}}_z=\frac{1}{2r}\Bigl(\frac{\partial }{\partial r}(r\bar{u}_θ)-\frac{\partial \bar{u}_r}{\partial θ}\Bigr)\tag{6.c}$$
波動方程式(4)の一般解を導くために、変位と物体力を周方向にフーリエ級数展開し、半径方向にはハンケル変換を行います。式(4)中の変位ベクトル \(\bar{\mathbf{U}}=\{\bar{u}_r,\bar{u}_θ,\bar{u}_z\}^T\) のフーリエ・ベッセル変換対は、
$$\tilde{\bar{\mathbf{U}}}(ξ,z)=α_n\int_{0}^{∞}r\mathbf{C}_n(ξr)\int_{0}^{2π}\mathbf{T}_n(θ)\bar{\mathbf{U}}(r,θ,z)dθdr\tag{7.a}$$
$$\bar{\mathbf{U}}(r,θ,z)=\sum_{n=0}^{∞}\mathbf{T}_n(θ)\int_{0}^{∞}ξ\mathbf{C}_n(ξr)\tilde{\bar{\mathbf{U}}}(ξ,z)dξ\tag{7.b}$$
であり、同様にして応力ベクトル \(\bar{\mathbf{f}}=\{\bar{f}_r,\bar{f}_θ,\bar{f}_z\}^T\) のフーリエ・ベッセル変換対は、
$$\tilde{\bar{\mathbf{f}}}(ξ,z)=α_n\int_{0}^{∞}r\mathbf{C}_n(ξr)\int_{0}^{2π}\mathbf{T}_n(θ)\bar{\mathbf{f}}(r,θ,z)dθdr\tag{8.a}$$
$$\bar{\mathbf{f}}(r,θ,z)=\sum_{n=0}^{∞}\mathbf{T}_n(θ)\int_{0}^{∞}ξ\mathbf{C}_n(ξr)\tilde{\bar{\mathbf{f}}}(ξ,z)dξ\tag{8.b}$$
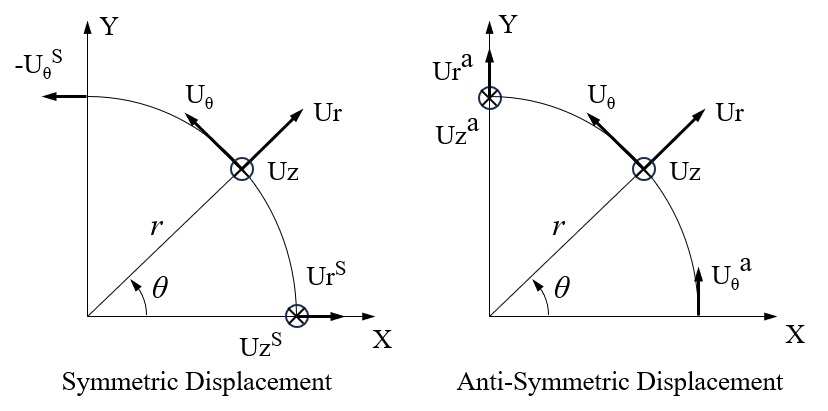
で与えられます。ただし、\(\tilde{\bar{\mathbf{U}}}(ξ,z)\) , \(\tilde{\bar{\mathbf{f}}}(ξ,z)\) は、それぞれラプラス・波数領域での変位と応力のフーリエ振幅であり、\(ξ\) は半径方向の波数を表わします。また、マトリックス \(\mathbf{T}_n(θ)\) は周方向へのフーリエ級数を定義し、x軸(\(θ=0°\))に対して対象な場合を肩添字 \(s\) 、逆対称(\(θ=90°\))の場合を肩添字 \(a\) として以下のように定義します。
$$\mathbf{T}_n^s(θ)=diag(\cos{\bar{nθ}} -\sin{\bar{nθ}} \cos{\bar{nθ}})\tag{9.a}$$
$$\mathbf{T}_n^a(θ)=diag(\sin{\bar{nθ}} \cos{\bar{nθ}} \sin{\bar{nθ}})\tag{9.b}$$
これば、下図のようにX軸上とY軸上に定義される振幅で周方向の応答を定義するもので、3次元問題を円筒座標系での疑似3次元として定義するものと考えられます。
また、変換マトリックス \(\mathbf{C}_n(ξr)\) は第1種n次のベッセル関数 \(J_n(ξr)\) によって、
$$ \mathbf{C}_n(ξr) = \begin{bmatrix} -\frac{1}{ξ}J_n(ξr)_{,r} & -\frac{n}{ξr}J_n(ξr) & 0 \\-\frac{n}{ξr}J_n(ξr) & -\frac{1}{ξ}J_n(ξr)_{,r}& 0\\0 & 0 & J_n(ξr) \end{bmatrix} \tag{10}$$
係数 \(α_n\) はつぎのように表されます。
$$ α_n=\begin{cases}\displaystyle\frac{1}{2π} &n=0\\ \displaystyle\frac{1}{π} &n≠0 \end{cases} \tag{11}$$
ラプラス・波数領域の支配方程式
支配方程式(3)にフーリエ・ベッセル変換(式(6)、式(7))を適用すると、各フーリエ次数 \(n\) に関するラプラス・波数領域での支配方程式がつぎのように導かれます。
$$μ\frac{d^2 \tilde{\bar{u}}_{1n}}{dz^2}-(λ+2μ)k_α^2・\tilde{\bar{u}}_{1n}-(λ+μ)ξ\frac{d^2 \tilde{\bar{u}}_{2n}}{dz^2}+\tilde{\bar{f}}_{1n}=0\tag{11.a}$$
$$(λ+μ)ξ\frac{d \tilde{\bar{u}}_{1n}}{dz}+(λ+2μ)\frac{d^2 \tilde{\bar{u}}_{2n}}{dz^2}-μk_β^2\tilde{\bar{u}}_{2n}+\tilde{\bar{f}}_{2n}=0\tag{11.b}$$
$$μ\frac{d^2 \tilde{\bar{u}}_{3n}}{dz^2}-μk_β^2\tilde{\bar{u}}_{3n}+\tilde{\bar{f}}_{3n}=0\tag{11.c}$$
ここに、
$$k_α=\sqrt{ξ^2+(p/V_p)^2} , k_β=\sqrt{ξ^2+(p/V_s)^2}\tag{12}$$
ただし、は圧縮波速度、はせん断波速度であり、
$$V_p=\sqrt{\frac{λ+2μ}{ρ}} , V_s=\sqrt{\frac{μ}{ρ}}\tag{13}$$
そして、第1添字 \((\enspace 1,\enspace 2,\enspace 3\enspace)\) は空間領域での \((\enspace r,\enspace z,\enspace θ\enspace)\) に対応しています。上式(11)は3次元波動場を \(r-z\) 面内で生じるP波とSV波の波動場とそれに直交方向 \(θ\) のSH波の波動場に分離できることを示しています。
変位の一般解
式(11)の変位の一般解はつぎのように表されます。
面内波に対して、
$$\begin{Bmatrix}\tilde{\bar{u}}_{1n}(ξ,z)\\ \tilde{\bar{u}}_{2n}(ξ,z)\end{Bmatrix}=\mathbf{A}\mathbf{E}_{sv-p}\{A_{P} A_{SV} B_{P} B_{SV}\}^T+\begin{Bmatrix}\hat{u}_{1n}(ξ,z)\\ \hat{u}_{2n}(ξ,z)\end{Bmatrix}\tag{14}$$
面外波に対して、
$$\tilde{\bar{u}}_{3n}(ξ,z)=\mathbf{E}_{sh}\{A_{SH} B_{SH}\}^T+\hat{u}_{3n}(ξ,z)\tag{15}$$
ここに、\(\mathbf{A}\) , \(\mathbf{E}_{sv-p}\) , \(\mathbf{E}_{sh}\) はそれぞれ、
$$ \mathbf{A} = \begin{bmatrix} -ξ & k_β & -ξ & k_β\\ -k_α & ξ & k_α & -ξ \end{bmatrix} \tag{16}$$
$$ \mathbf{E}_{sv-p} = diag(e^{-k_αz} e^{-k_βz} e^{k_αz} e^{k_βz}) \tag{17}$$
$$ \mathbf{E}_{sh} = \{e^{-k_βz} e^{k_βz}\} \tag{18}$$
です。係数 \(A\) , \(B\) は未知数であり、\(A_P\) , \(A_{SV}\) , \(A_{SH}\) はそれぞれP波、SV波、SH波の下降波、\(B_P\) , \(B_{SV}\) , \(B_{SH}\) はそれぞれP波、SV波、SH波の上昇波に関するものです。また、上式(14),(15)の右辺第1項は自由振動解を、第2項 \(\{\hat{u}_{1n},\enspace \hat{u}_{2n},\enspace \hat{u}_{3n}\}\) は加振源による強制振動解を表わしています。
応力の一般解についても変位と同様にして、自由振動解と強制振動解の和としてつぎのように表わされます。
面内波に対して、
$$\begin{Bmatrix}\tilde{\bar{σ}}_{12n}(ξ,z)\\ \tilde{\bar{σ}}_{22n}(ξ,z)\end{Bmatrix}=\mathbf{B}\mathbf{E}_{sv-p}\{A_{P} A_{SV} B_{P} B_{SV}\}^T+\begin{Bmatrix}\hat{σ}_{12n}(ξ,z)\\ \hat{σ}_{22n}(ξ,z)\end{Bmatrix}\tag{19}$$
面外波に対して、
$$\tilde{\bar{σ}}_{32n}(ξ,z)=\mathbf{C}\mathbf{E}_{sh}\{A_{SH} B_{SH}\}^T+\hat{σ}_{32n}(ξ,z)\tag{20}$$
ここに、
$$ \mathbf{B} = μ\begin{bmatrix} 2ξk_α & -(ξ^2+k_β^2) & -2ξk_α & ξ^2+k_β^2\\ξ^2+k_β^2 & -2ξk_β & ξ^2+k_β^2 & -2ξk_β \end{bmatrix} \tag{21}$$
$$ \mathbf{C} = μ\begin{bmatrix} -k_β & 0\\0 & k_β \end{bmatrix} \tag{22}$$
次回は剛基盤上の一様成層地盤における基本解を誘導します。


コメント