物体力と応力テンソルの成分が 1 つの空間変数、たとえば \(x_1\) のみに依存する場合、応力の運動方程式は次のように縮合されます。
$$τ_{i1,1}+ρf_i=ρ\ddot{u}_i\tag{46}$$
1次元問題では以下の3 つのケースが考えられます。
軸方向ひずみ状態
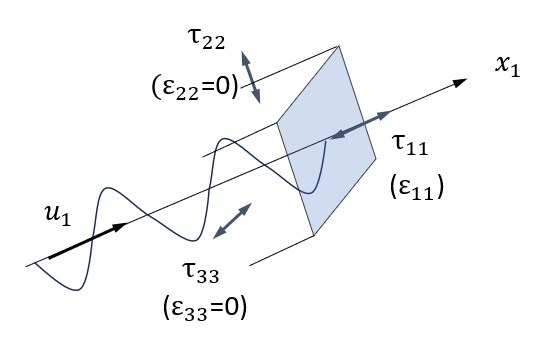
すべての変位成分のうち、軸方向の変位 \(u_1(x_1,t)\) だけが残り、ひずみ成分は \(ε_{11}=\partial{u}_1/\partial{x}_1\) のみとなります。式(28)から応力テンソルの成分は次のように得られます。
$$τ_{11}=(λ+2μ)u_{1,1} , τ_{22}=τ_{33}=λu_{1,1}\tag{47}$$
そして運動方程式は、
$$(λ+2μ)u_{1,11}+ρf_1=ρ\ddot{u}_1\tag{48}$$
軸方向応力状態
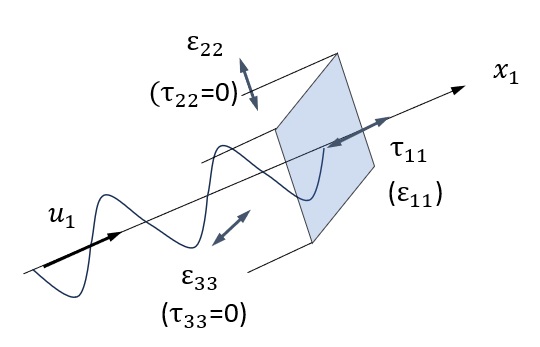
\(u_1\) と \(t\) の関数である軸方向直応力 \(τ_{11}\) は、消失しない応力成分です。軸直角方向直応力 \(τ_{22}\) と \(τ_{33}\) をゼロにすると、次の関係が得られます。
$$ε_{22}=ε_{33}=-\frac{λ}{2(λ+μ)}ε_{11}=-νε_{11}\tag{49}$$
ここで、\(ν\) はポアソン比です。続いてこれらの結果を \(τ_{11}\) の式に置き換えると、次のようになります。
$$τ_{11}=Eε_{1,1}\tag{50}$$
ここで、
$$E=\frac{μ(3λ+2μ)}{λ+μ}\tag{51}$$
定数 \(E\) はヤング係数です。式(50) を 式(46) に代入すると、運動方程式が得られます。
せん断状態
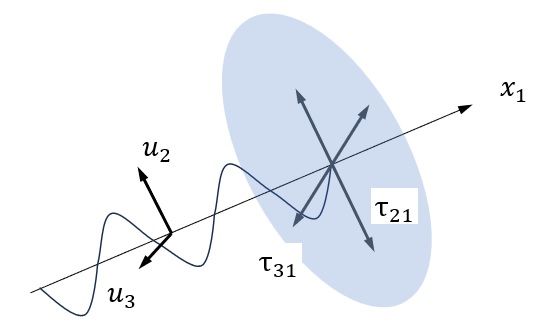
\(x_1\) 軸に垂直な平面内の変位が存在する場合、
$$\mathbf{u}=u_2(x_1,t)\mathbf{i}_2+,u_3(x_1,t)\mathbf{i}_3$$
それらによる応力は、
$$τ_{21}=μu_{2,1} , τ_{31}=μu_{3,1}$$
明らかに、運動方程式はそれぞれ \(u_2\) と \(u_3\) の独立な波動方程式に帰着します。
今回は以上です。


コメント