表面力と物体力は、運動エネルギーを物体に伝達します。外力が及ぼした仕事の率(単位時間当たりのエネルギー伝達)のことは仕事率と呼ばれます。境界 \(S\) のある規則的な領域 \(V\) を占める物体 \(B\) の場合、仕事率は表面力と物体力の和として次のように表すことができます。
$$P=\int_{S}t_i\dot{u}_i\enspace dA+\int_{V}ρf_i\dot{u}_i\enspace dV\tag{61}$$
ここで、コーシーの応力公式 \(t_{i}=τ_{ij}n_{j}\) を使用してガウスの発散定理を利用すると、次のように書き換えることができます。
$$P=\int_{V}[(τ_{ij}\dot{u}_i)_{,j}+ρf_i\dot{u}_i]\enspace dV\tag{62}$$
さらに式(62)を評価するために、\(u_{i,j}\) を次のように分解します。
$$\dot{u}_{i,j}=\dot{ε}_{ij}+\dot{ω}_{ij}\tag{63}$$
ここで、\(εij\) と \(ωij\) は式(19)と式(20)にそれぞれ定義されています。反対称テンソルの \(ωij\) の項が消えるので、\(τ_{ij}u_{i,j}\) は対称テンソル \(εij\) の項のみとなり次のように書くことができます。
$$τ_{ij}\dot{u}_{i,j}=τ_{ij}\dot{ε}_{ij}\tag{64}$$
※式(19)と式(20)はこちら ⇓
式(64) と運動方程式 (39) により、仕事率の式は次のようになります。
$$P=\int_{V}ρ\ddot{u}_i\dot{u}_i\enspace dV+\int_{V}τ_{ij}\dot{ε}_{ij}\enspace dV\tag{65}$$
※式(39)はこちら ⇓
物体の運動エネルギーは次のように定義されます。
$$K=\frac{1}{2}\int_{V}ρ\dot{u}_i\dot{u}_i\enspace dV\tag{66}$$
これから仕事率はつぎのように表わされます。
$$P=\frac{dK}{dt}+\int_{V}τ_{ij}\dot{ε}_{ij}\enspace dV$$
線形弾性である場合、物体の全ひずみエネルギーは、
$$U=\frac{1}{2}\int_{V}τ_{ij}ε_{ij}\enspace dV\tag{67}$$
Uの時間微分はフックの法則からつぎのようになります。
$$\frac{dU}{dt}=\frac{1}{2}\int_{V}(\dot{τ}_{ij}ε_{ij}+τ_{ij}\dot{ε}_{ij})\enspace dV=\int_{V}τ_{ij}\dot{ε}_{ij}\enspace dV$$
以上から線形弾性体では、
$$P=\frac{dK}{dt}+\frac{dU}{dt}\tag{68}$$
式(68)は、弾性体の場合、表面力と物体力の作用により物体に流入するエネルギーが運動エネルギーとひずみエネルギーに変換されることを示しています。
静止状態にあった物体の場合、式(68) は \(0\) から \(t\) の間で時間の経過とともに積分され、エネルギーの同一性が得られます。
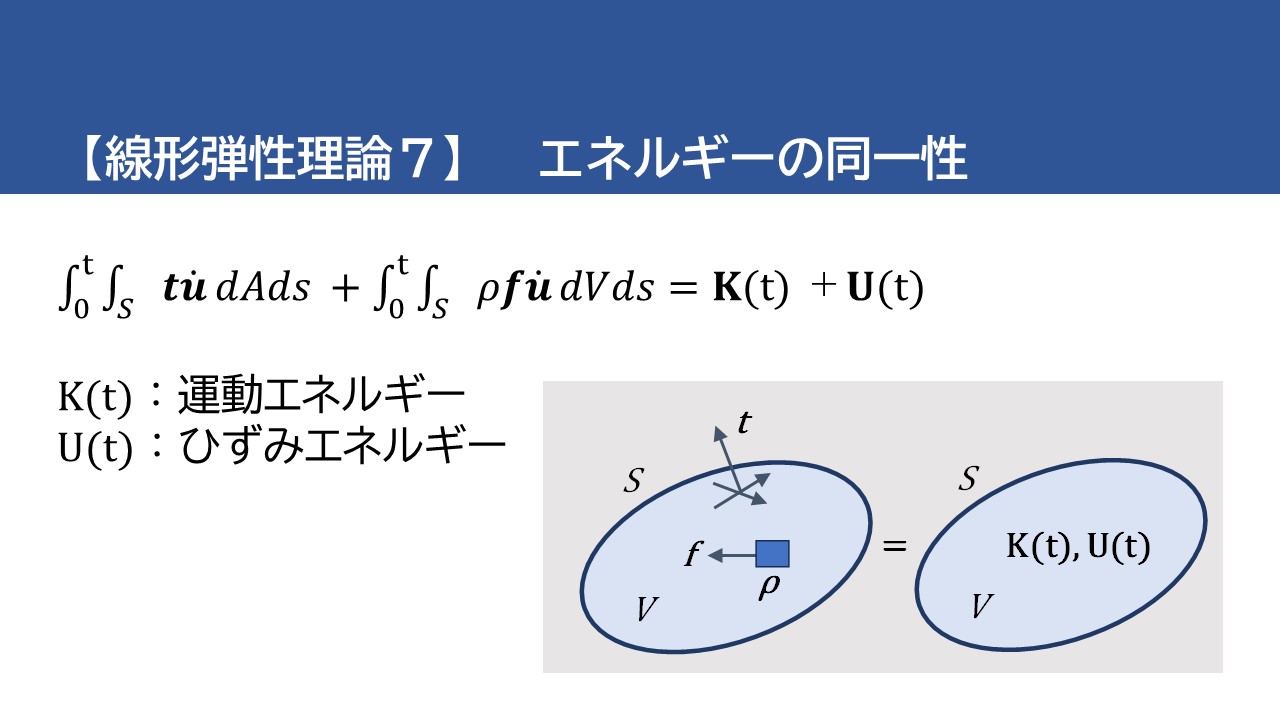
$$\int_{0}^{t}\int_{S}\mathbf{t}(\mathbf{x},s)・\dot{\mathbf{u}}(\mathbf{x},s)\enspace dAds+\int_{0}^{t}\int_{V}ρ\mathbf{f}(\mathbf{x},s)・\dot{\mathbf{u}}(\mathbf{x},s)\enspace dVds=K(t)+U(t)\tag{69}$$
ここで、\(K(t)\) は運動エネルギー、\(U(t)\) はひずみエネルギーをそれぞれ表わします。
今回は以上です。



コメント