一般に波動方程式を導く場合には、Navior式から始めることが多いのではないでしょうか?しかし、わたしが学生の時に勉強した1973年初版の”Wave propagartion in elastic solids”では、連続体力学から解説が始まっていますので、少し我慢して一次元非線形連続力学から勉強したいと思います。
今回は、主に連続体のオイラー表現(空間表示)、ラグランジュ表現(物質表示)について示します。
運動の表示
連続体力学では、物体を微少な粒子(物質点)の連続的な集合体と考えます。一次元の縦(軸)方向の運動は、すべての物質粒子が平行に移動します。連続体の 1 次元の縦方向の運動を記述するには、軸(長さ)方向の座標と時間があれば十分です。ある時刻、たとえば \(t=0\) における物質点 \(P\) の位置が座標 \(X\) にあるとします。その後の時間 \(t\) での物質粒子の位置を、座標\(X\)の関数として次のように表します。
$$x=P(X,t)\tag{1}$$
同式は運動の物質表示と呼ばれます。 \(X\) と \(t\) が独立変数であるこの表示は、しばしばラグランジュ表示(各粒子とともに移動する観察者から見た運動表示)とも呼ばれます。上式の独立変数 \(X\) の値は、その物質粒子の基準位置として常に物質粒子を識別するものとなります。従属変数 \(x\) の値は、基準位置を \(X\) とした物質粒子の現在位置を表します。
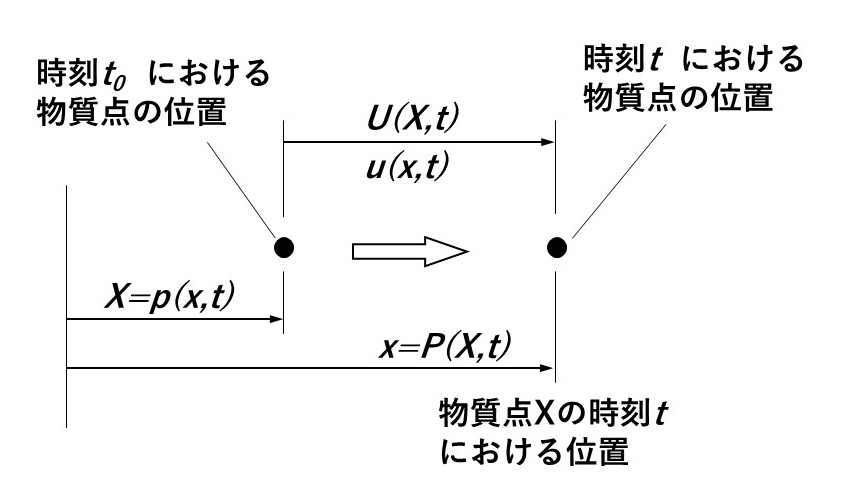
一方で、運動を空間表示で記述することもできます。オイラー表示(空間に固定された点から見た運動表示)とも呼ばれる表示では、独立変数である時間 \(t\) と位置 \(x\) を用いてつぎのように表します。
$$X=p(x,t)\tag{2}$$
上式では、独立変数 \(x\) の値が物質粒子の現在の位置を指定します。従属変数 \(X\) は、現在位置 \(x\) に位置する物質粒子の基準位置を表します。もちろん、運動の2つの記述は互いに一貫していなければなりません。つまり、上式は \(X\) に対して式(1) を解くことで得られ、またその逆も同様です。
独立変数に対する場を識別するために、基準位置 \(X\) および 時間 \(t\) で表される物質表示には大文字を、現在の位置 \(x\) および 時間 \(t\) で表される空間表示には小文字を使用します。
たとえば、変位は物質表示では \(U(X,t)\) で示され、空間表示では \(u(x,t)\) で示されます。
$$U(X,t)=P(X,t)-X\tag{3}$$
$$u(x,t)=x-p(x,t)\tag{4}$$
変形
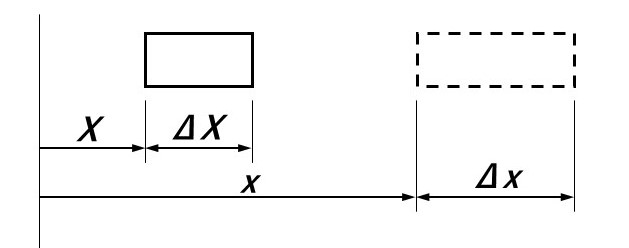
要素の1次元の運動を図で示します。運動の方向の不均一性の結果として、要素は変形を受けます。1 次元の場合、変形の最も単純な尺度は、同じ物質粒子で構成される要素の伸びを元の長さで割ったものです。したがって、この変形率は \((Δx-ΔX)/ΔX\) で表すことができます。限界値として、
$$\lim_{ΔX\rightarrow0}\frac{Δx-ΔX}{ΔX}=\frac{\partial U}{\partial X}\tag{5}$$
となり、物質表示における変形率として変位勾配 \({\partial U}/{\partial X}\) が得られます。3 次元の変形では、変形率として長さ要素の 2 乗の差を取る方が便利であり、これはラグランジュひずみテンソルと呼ばれます。1 次元では、ラグランジュひずみは次のようになります。
$$E=\frac{1}{2}\lim_{ΔX\rightarrow0}\frac{(Δx)^2-(ΔX)^2}{(ΔX)^2}=\frac{\partial U}{\partial X}+\frac{1}{2}\Bigl(\frac{\partial U}{\partial X}\Bigr)^2\tag{6}$$
もちろん、変形は空間座標系でも記述できます。弾性体の場合、外部荷重が取り除かれると物質粒子が戻る未変形の基準状態が常に存在するため、変形の表現は式(5)と式(6)が一般的です。
時間変化率
物質粒子の速度は、一定の基準位置 \(X\) に対応する物質粒子位置 \(x=P(X,t)\) の時間変化率としてつぎのように表されます。
$$V(X,t)=\frac{\partial P(X,t)}{\partial t}\tag{7}$$
同式は粒子速度の物質表示であり、特定の物質粒子の速度を時間の関数として与えられます。空間表示では、物質粒子の速度は式(2)の \(X\) を式(7)に代入することで次のように得られます。
$$v(x,t)=V[ p(x,t),t ]\tag{8}$$
上式は、固定した空間位置 \(x\) において、時間 \(t\) に \(x\) を通過する特定の粒子の速度 \(v\) を定義しています。多くの場合、連続体の瞬間的な動きは、位置 \(x\) に瞬間的に位置する粒子の変位 \(u(x,t)\) によって記述されます。このとき、ある時間 \(t\) において \(x\) に位置した物質粒子は \(Δt\) 時間後に \(x+vΔt\) に移動しますので(粒子位置に関しては \(x\) と \(t\) の関数)、瞬間速度は微分連鎖律を使用して次のように表されます。
$$v=\frac{\partial u}{\partial t}+v\frac{\partial u}{\partial x}\tag{9}$$
式(9)で表される演算は通常 \(D/Dt\) で表され、すなわち、
$$\frac{D}{Dt}=\frac{\partial}{\partial t}+v\frac{\partial}{\partial x}\tag{10}$$
式(7)と(9)では、偏導関数 \(\partial/\partial t\) は、他の変数を固定値として時間に関して微分を行う導関数です。一般に、他の変数が物質表示か空間表示かの区別は明らかで、大文字の記号は物質表示 \(X\) および \(t\) で表される場の量を表し、小文字の記号は空間表示 \(x\) と \(t\) で表される場の量を表しています。
物質表示での加速度は次のように定義されます。
$$A=\frac{\partial V(X,t)}{\partial t}\tag{11}$$
粒子速度を位置 \(x\) と時間 \(t\) の関数として表すと、空間表示で次のようになります。
$$a=\frac{Dv}{Dt}=\frac{\partial v}{\partial t}+v\frac{\partial v}{\partial x}\tag{12}$$
質量保存と線形運動量(速度と質量の積)のつり合いを調べるためには、線積分の時間変化率を評価する必要があります。空間表示では、移動質量系を含む固定領域 \(x_1≦x≦x_2\) を考慮します。質量系によって瞬間的に運ばれるシステムの全体量 \(f(x,t)\) の合計は、次の式で与えられます。
$$\int_{x_1} ^ {x_2} f(x,t)dx$$
積分の時間変化率は、領域内に瞬間的に位置する \(f(x,t)\) の増加率と \(f(x,t)\) の境界上での外向き内向きの速度差の 2 つの項で構成されます。これは次の形式で表されます。
$$\frac{d}{dt}\int_{x_1} ^ {x_2} f(x,t)dx=\int_{x_1} ^ {x_2} \frac{\partial f}{\partial t}dx+f(x,t)v(x,t)|_{x=x_1} ^ {x=x_2}\tag{13}$$
式(13)の左側は、空間領域 \(x_1≦x≦x_2\) 内に瞬間的に位置する量 \(f(x,t)\) の合計の時間増加率を表します。式(13)はレイノルズの輸送定理の一次元バージョンで、次のように書き換えられます。
$$\frac{d}{dt}\int_{x_1} ^ {x_2} f(x,t)dx=\int_{x_1} ^ {x_2} \biggl[\frac{\partial f}{\partial t}+\frac{\partial}{\partial x}(fv)\biggr]dx\tag{14}$$
以上、一次元非線形連続力学の運動の表示、変形、時間変化率について勉強しましたが、ちょっと時間が掛かりました。次回は、質量保存、運動量のつり合い、エネルギーのつり合いについて勉強したいと思います。

コメント