【線形弾性理論１】表記法と数学の予備知識

　線形弾性体の運動方程式を示していきます。初回となる今回は、テンソル、スカラー、ベクトル、外積、内積等のベクトル演算子、それからガウスの定理（発散定理）について示していきます。

線形弾性理論の概要
表記法と数学的予備知識

線形弾性理論の概要

　弾性体は、すべての外部荷重が取り除かれると元の変形していない状態に戻ります。したがって、材料を時間と変形前の基準位置に独立な変数として、弾性体の変形を記述できる利点があります。また、3次元弾性体の運動は正確には強い材料非線形性を示しますが、弾性体における多くの波動伝播効果が、線形化された理論によって適切に表現できることが幅広い経験によって知られています。
　1 次元幾何学の一般理論、線形化理論と線形化の条件については“弾性連続体の１次元運動”で説明しましたので、非線形理論と 3 次元環境における線形化を詳細に扱うことは行いません。したがって、変位成分の空間勾配が1よりもはるかに小さい、およびCaucyの応力テンソルのすべての成分が同じオーダーの大きさであるとして、材料を線形弾性に限定します。さらに、速度と加速度の空間記述における対流項（ナビヤ・ストークス式の変位と座標微分の積からなる項）は無視できるとします。そうすると、物質的記述と空間的記述間の差異はなくなり、従属フィールド変数と独立フィールド変数の1つのシステムを採用するだけで十分になります。
　線形弾性理論の詳細な扱いについては、他を参照してください。ただし、基本方程式は参考のためにここで簡単にまとめますが、動的問題に関連するいくつかのトピックについては、より詳細に説明します。また、直交座標、球座標、および円筒座標の線形方程式の概要や、理想流体の支配方程式についても簡単に説明します。

表記法と数学的予備知識

　物理法則を記述する方程式はテンソル方程式であり、物理量はさまざまな次数のテンソルによって数学的に表現されます。特別な方向に関連付けられておらず、単一の数値によって測定される量はスカラー、つまりゼロ次のテンソルによって表されます。次数1のテンソルはベクトルであり、方向と大きさによって特徴付けられる量を表します。より複雑な物理量は、1より大きい次数のテンソルで表されます。以下では、通常のローマ字またはギリシャ文字はスカラーを表し、太字のローマ字はベクトルを示し、太字の小文字のギリシャ文字は 2 次テンソルを示します。

記号表記

　理論を説明するには、固定直交デカルト座標系で十分です。指標表記では、座標軸は $x_j$ で表され、基底ベクトルは $ij$ で表されます ( $j=1,2,3$ )。以降では、明示的に指定されない限り、添字は値 $1,2,3$ を想定します。ベクトル $u$ の各成分を $u_j$ で表せば、

$$\mathbf{u}=u_1\mathbf{i}_1+u_2 \mathbf{i}_2+u_3 \mathbf{i}_3\tag{1}$$

式(1)の合計は連続媒体の力学の数学的記述で頻繁に発生するため、添え字を変数で表記することで添字成分に関する合計を意味する総和規約を導入します。つまり式(1)は次のように書き換えることができます。

$$\mathbf{u}=u_j\mathbf{i}_j\tag{2}$$

総和規約の別の例として、2 つのベクトルのスカラー積は次のように表されます。

$$\mathbf{u}･\mathbf{v}=u_jv_j=u_1v_1+u_2v_2+u_3v_3\tag{3}$$

$u_j$ の添え字の値は $1,2,3$ のいずれかをとりますが、式(2)と式(3)の添え字 $j$ は３つの値 $1,2,3$ をすべてとらなければなりません。
　$τ_{ij}$ など2つの添字を持つ量は階数2のテンソル $\mathbf{τ}$ の成分を示し、同様に 3 つの添字を持つ量は階数3のテンソルを定義します。階数２のよく知られた特殊テンソルはクロネッカーデルタであり、その成分は次のように定義されます。

$$δ_{ij}=\begin{cases}1　　if　i=j　\\0　　if　i≠j\end{cases}\tag{4}$$

頻繁に使用される階数３の特別なテンソルは交代(alternating)テンソルで、そのコンポーネントは次のように定義されます。

$$e_{ijk}=\begin{cases}+1　　ijkが偶置換(123,231,312)の場合\\　0　　ijkの2つが同じ数の場合\\-1　　ijkが奇置換(321,213,132)の場合\end{cases}\tag{5}$$

交代テンソルと総和規約を使用すると、外積 $\mathbf{h}=\mathbf{u}\wedge\mathbf{v}$ の成分は次のように表すことができます。

$$h_i=e_{ijk}\enspace u_j\enspace v_k\tag{6}$$

つまり、$\mathbf{h}$ の個々の成分は次のようになります。

$$\begin{cases}h_1=u_2v_3-u_3v_2\\h_2=u_3v_1-u_1v_3\\h_3=u_1v_2-u_2v_1\end{cases}$$

ベクトル演算子

ベクトル計算で特に重要なのは、ベクトル演算子 $\mathbf{∇}$ （ナブラ）で次のように表されます。

$$\mathbf{∇}=\mathbf{i}_1 \frac{\partial}{\partial x_1}+\mathbf{i}_2 \frac{\partial}{\partial x_2}+\mathbf{i}_3 \frac{\partial}{\partial x_3}\tag{7}$$

スカラー場 $f(x1,x2,x3)$ に適用すると、ベクトル演算子 $\mathbf{∇}$はスカラー場の勾配として知られるベクトル場を生成します。

$$grad\enspace f=\mathbf{∇}f=\mathbf{i}_1 \frac{\partial f}{\partial x_1}+\mathbf{i}_2 \frac{\partial f}{\partial x_2}+\mathbf{i}_3 \frac{\partial f}{\partial x_3}$$

添字表記では次のように偏微分はカンマで行うのが一般的であり、

$$grad\enspace f=\mathbf{∇}f=\mathbf{i}_p\enspace f,_p\tag{8}$$

$f,_p$ 内の単一の添字の出現は、$f,_p$ が階数１のテンソル、つまりベクトルの成分であることを示します。
　$\mathbf{u}(x)$ で示されるベクトル場では、ベクトルの成分は空間座標の関数であり、$u_i(x_1,x_2,x_3)$ と表わされます。関数 $u_i(x_1,x_2,x_3)$ が微分可能であると仮定すると、9つの偏導関数 $∂u_i(x_1,x_2,x_3)/ ∂x_j$ は $u_{i,j}$ と表記することができ、2 階のテンソル成分であることが分ります。
　ベクトル演算子 $\mathbf{∇}$ がスカラー倍算と同様の方法でベクトルに対して演算されると、結果はベクトル場 $\mathbf{u}(x)$ の発散（ダイバージェンス）と呼ばれるスカラー場になります。

$$div\enspace \mathbf{u}=\mathbf{∇}･\mathbf{u}=u_{i,j}\tag{9}$$

$\mathbf{∇}$ と $\mathbf{u}$ の外積を取ることで $\mathbf{u}$ のカールと呼ばれるベクトルが得られ、curl $\mathbf{u}$ または $\mathbf{∇}\wedge\mathbf{u}$ で表されます。$\mathbf{q}$=$\mathbf{∇}\wedge\mathbf{u}$ の場合、$\mathbf{q}$ の成分は次のようになります。

$$q_i=e_{ijk}\enspace u_{k,j}\tag{10}$$

ラプラス演算子 $\mathbf{∇}^2$ は、勾配の発散を取ることによって取得されます。2 回微分可能なスカラー場のラプラシアンは、別のスカラー場であり、

$$div\enspace grad\enspace f=\mathbf{∇}･\mathbf{∇}f=f_{,ii}\tag{11}$$

ベクトル場のラプラシアンは、 $\mathbf{∇}^2\mathbf{u}$ で示される別のベクトル場です。

$$\mathbf{∇}^2\mathbf{u}=\mathbf{∇}･\mathbf{∇}\mathbf{u}=u_{p,jj}\mathbf{i}_p\tag{12}$$

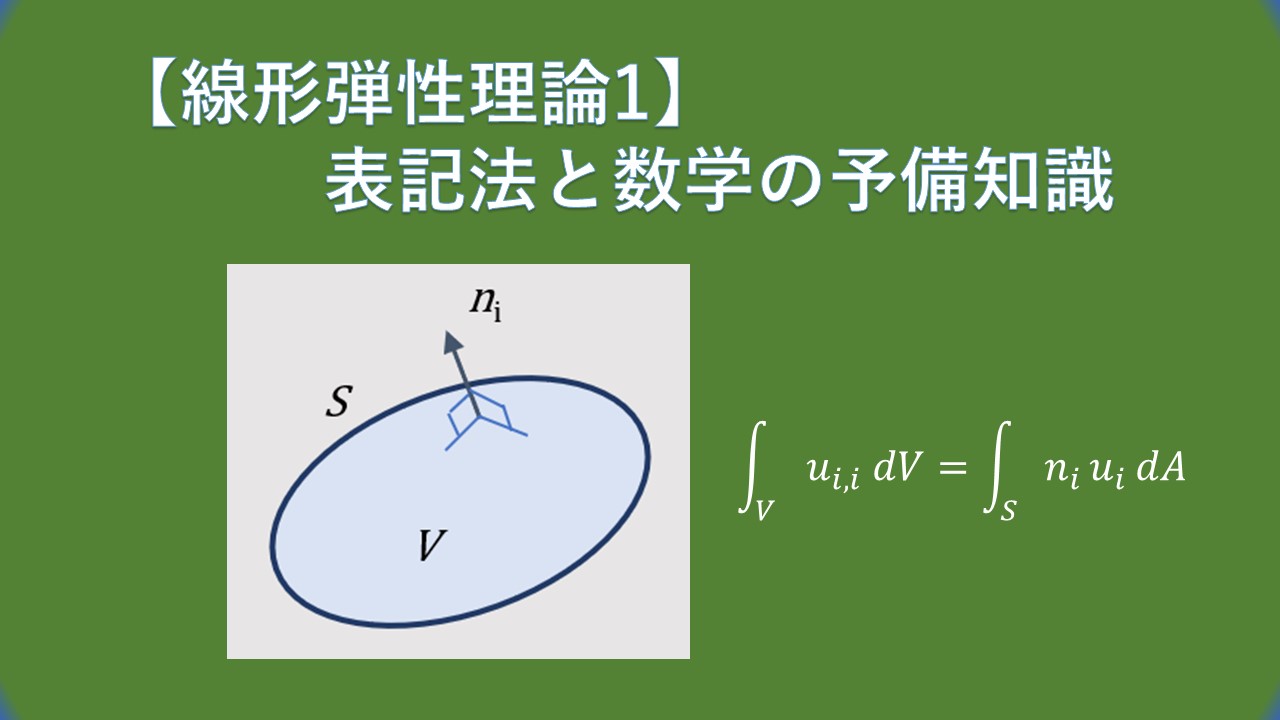
ガウスの定理（発散定理）

　テンソル解析における最も重要な積分定理について述べます。ガウスの定理として知られるこの定理は、体積積分を体積の境界面上の表面積分に関連付けます。区分的に連続的に回転する接平面を持つ表面 $S$ によって境界付けられた体積 $V$ の凸領域 $B$ を考えてみましょう。このような領域を規則的であると言います。ここで、テンソル場 $τ_{jkl…p}$ を考え、$τ_{jkl…p}$ のすべての成分が $B$ で連続微分可能であるとします。すると、ガウスの定理は次のようになります。

$$\int_{V}τ_{jkl…p\enspace ,i}\enspace dV=\int_{S}n_i\enspace τ_{jkl…p}\enspace dS\tag{13}$$

ここで、$n_i$ は表面 $S$ の外側法線に沿った単位ベクトルの成分です。ベクトル $\mathbf{u}$ の 3 つの成分を $τ_{jkl…p}$ に代入して式(13) を記述し、結果として得られる 3 つの方程式を合わせると、結果は次のようになります。

$$\int_{V}u_{i,i}\enspace dV=\int_{S}n_i\enspace u_i\enspace dA\tag{14}$$