地震応答スペクトル計算(1)に示した1自由度系の運動方程式を中央差分法で時刻歴解析を行い、地震応答スペクトルを求めてみます。ExcelはOffice2021を用いました。
中央差分法の定式化
地震応答スペクトル計算(1)に示した1自由度系の運動方程式は、
$$\ddot{u}+2hω_0\dot{u}+ω_0^2u=-\ddot{u}_G\tag{1}$$
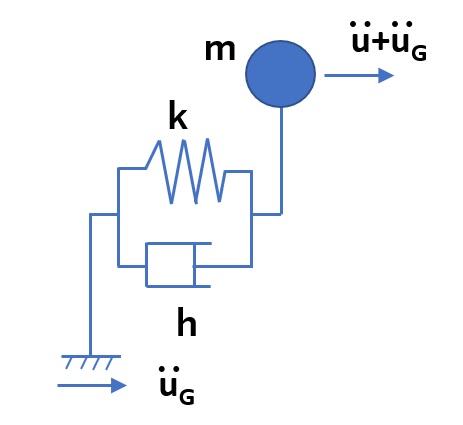
ここで、\(ω_0\) は構造物の固有角振動数、\(h\) は減衰比です。相対変位 \(u\) 、相対速度 \(\dot{u}\) 、相対加速度 \(\ddot{u}\) 、地震波加速度 \(\ddot{u}_G\) はそれぞれ時間の関数ですが、地震波の時間刻み \(Δt\) を使って離散化し、\(t=nΔt\) における変位、速度、加速度をつぎのように表します。
相対変位 \(u_n=u(nΔt)\) , 相対速度 \(\dot{u}_n=\dot{u}(nΔt)\)
相対加速度 \(\ddot{u}_n=\ddot{u}(nΔt)\) , 地震波加速度 \(\ddot{u}_Gn=\ddot{u}(nΔt)_G\)
この表記を用いると、\(t=nΔt\) における1自由度系の運動方程式は、
$$\ddot{u}_n+2hω_0・\dot{u}_n+ω_0^2・u_n=-\ddot{u}_{Gn}\tag{2}$$
さて、中央差分法を用いて、速度および加速度を変位で表すと、
$$\dot{u}_n=\frac{u_{n+1}-u_{n-1}}{2Δt}\tag{3}$$
$$\ddot{u}_n=\frac{\displaystyle\frac{u_{n+1}-u_n}{Δt}-\frac{u_n-u_{n-1}}{Δt}}{Δt}$$
$$=\frac{u_{n+1}-2u_n+u_{n-1}}{Δt^2}\tag{4}$$
式(3)、式(4)を式(2)に代入して変形すると、
$$\frac{u_{n+1}-2u_n+u_{n-1}}{Δt^2}+2hω_0・\frac{u_{n+1}-u_{n-1}}{2Δt}+ω_0^2・u_n=-\ddot{u}_{Gn}$$
$$∴u_{n+1}=\frac{A_1・u_n+A_2・u_{n-1}-\ddot{u}_{Gn}・{Δt^2}}{A_3}\tag{5}$$
$$A_1=2-ω_0^2・Δt^2 , A_2=hω_0・Δt-1 , A_3=1+hω_0・Δt\tag{6}$$
式(5)、式(6)より、初期値 \(u_{-1}=u_0=0\) として相対変位を求め、これを式(3)、式(4)に代入して相対速度および相対加速度を求めます。なお、加速度は相対加速度と地震加速度の和 \((\ddot{u}_n+\ddot{u}_{Gn})\) として絶対加速度の値を求めます。
応答スペクトルは、構造物の各固有周期に対して応答値の最大値をプロットしたものであるので、上記の方法で求めた時刻歴応答値より絶対値の最大値をそれぞれ求めていきます。
メインプロシージャ
メインのプロシージャ部を示します。
- 計算条件のインプットを”Sub 入力データ”にてワークシート”Input”から読み取った後、
- 地震波データの読み込みを行います。この”Sub 地震データ読み込み”については、VBAで地震波時刻歴のテキストデータを読み込んで図化用データをつくる!にて作成したプロシージャを利用しており、テキストデータから直接データを読み取ります。
- 応答スペクトル結果をワークシート”応答スペクトル”に書き込む準備を行って、
- ”入力データ”にて設定した固有周期毎に、”Sub 中央差分法”にて時刻歴応答を解析し、
- 絶対値の最大応答を求めて”Sub 中央差分法”内にて、ワークシート”応答スペクトル”に書き込んでいきます。
応答値のディメンジョンは、時刻歴データ数”16384”だけ設定していますが、後で時刻歴応答値をチェックするために設定しました。応答スペクトルを求めるためには、前後3ステップの応答値が分かれば良いので、”16384”は必要ありません。


計算条件のインプット
計算条件は、固有周期の最小値、最大値とその間の分割数、減衰比をワークシート”Input”内に書き込んでおき、それを”Sub 入力データ”にて読み込みます。
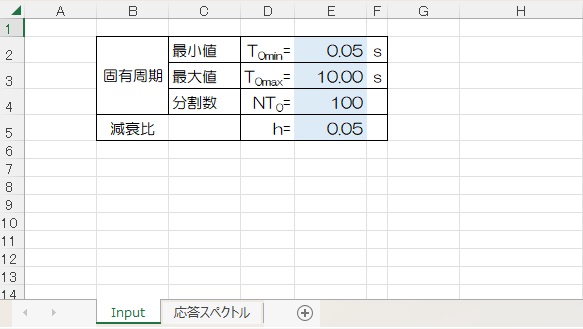
固有周期の計算ピッチは、対数上で等ピッチになるように”Sub 入力データ”内で設定しています。

なお、常用対数\(log_{10}\)は関数として準備されていないので、Functionにて定義しました。

中央差分法の計算
中央差分法の定式化に従って時刻歴応答を計算し、絶対値の最大値を求めています。求めた結果は、ワークシート”応答スペクトル”に書き込んでいます。

計算結果
下図の地震波に対して、応答スペクトルを算定しました。
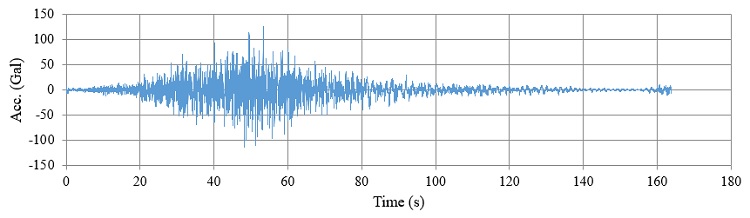
減衰比は0.05、固有周期は0.05~10.00sを100分割しました。
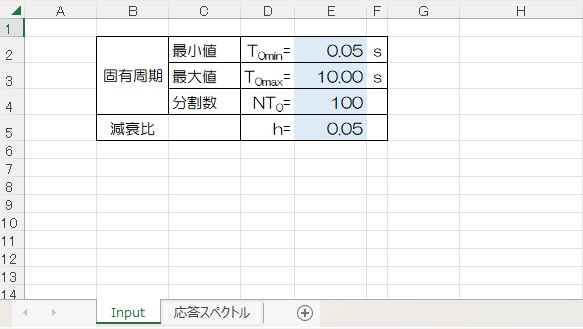
結果はワークシート”応答スペクトル”につぎのように出力され、絶対加速度、相対速度、相対変位をそれぞれグラフ化しています。
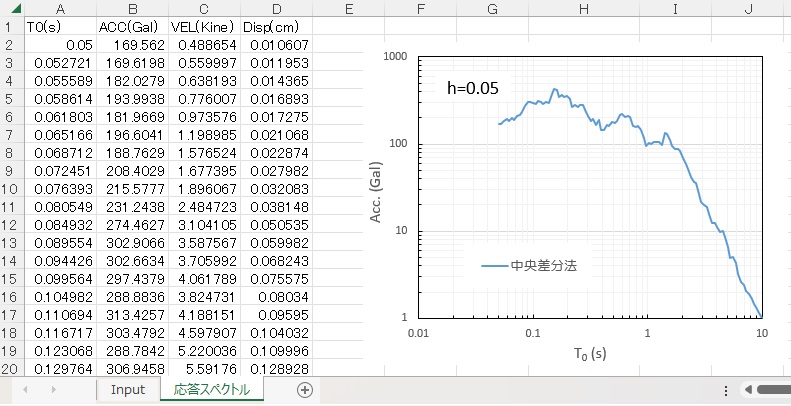
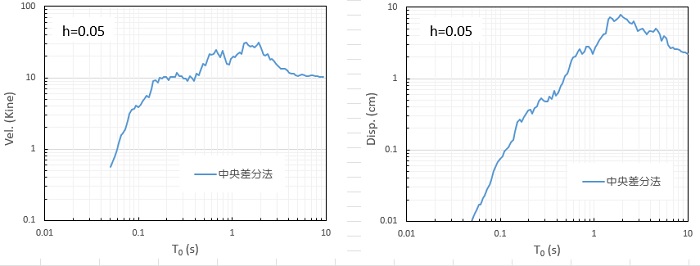
他の計算結果と検証をしていますが、ほぼ問題ない精度であるようです。ただし、固有周期が0.05sよりも小さくなるとオーバーフローしてしまいますので、中央差分法には若干の不満が残りました。応答スペクトルとしては、もう少し小さい周期まで計算したいものです。
つぎは、もう少し精度が良い線形加速度法にて計算してみたいと思います。

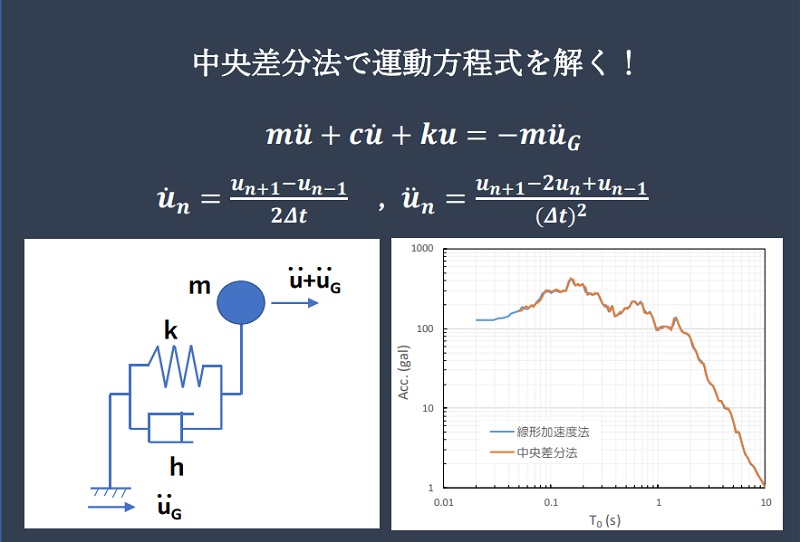





コメント