円形基礎や八角形基礎などの基礎反力を求めていきます。このシリーズでは、基礎反力の計算式を定式化したあと、ExcelVBAで繰り返し収束計算部分を作成していきたいと思います。まず、ここでは計算上の仮定に基づいて一般解を導き、左右対称である矩形断面の基礎反力から一般解を確認します。
算定上の仮定
基礎反力を算定するに当たり、つぎの仮定を設定します。
- 基礎形状は対称であり、その対称軸上に基礎反力(鉛直反力)が分布する。
- 基礎反力は対称軸上を直線に分布する。
- 基礎反力は奥行き方向に同一の値である。
- 鉛直荷重は、対称軸上の基礎重心から偏心距離\(e\)だけ離れた位置に集中荷重\(P\)を与える。
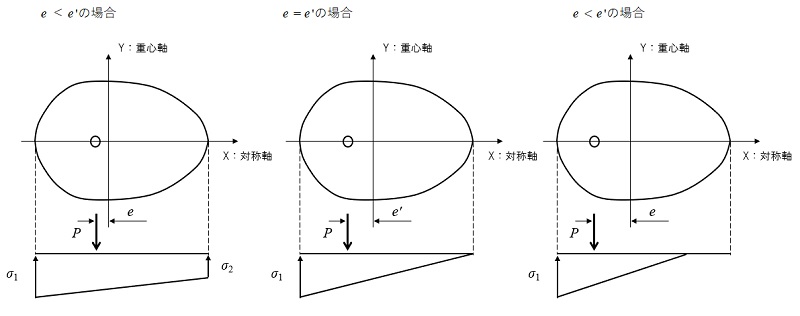
基礎反力を算定する際は、つぎの2つの場合に分けて考えます。
- 基礎全面に反力が発生している場合(対称軸上で台形分布)
- 基礎の一部分に反力が発生している場合(対称軸上で三角形分布)
2つのケースの変化点となる重心から荷重までの距離を偏心距離\(e’\)で表します。
基礎反力の一般解
基礎全面に反力が発生している場合
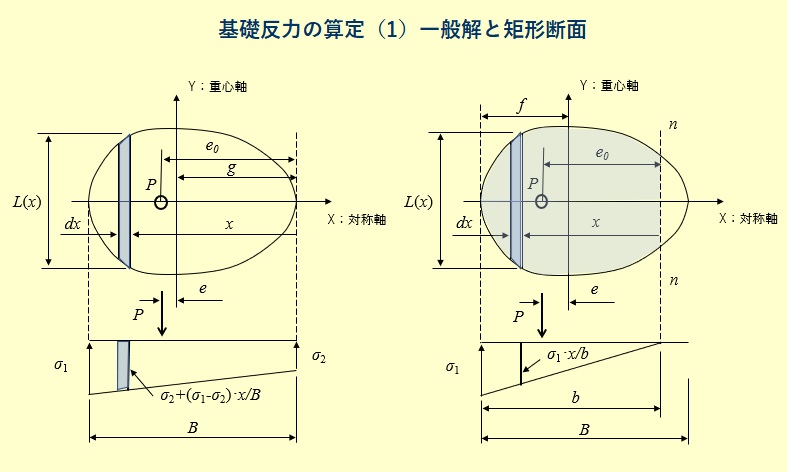
下図のように基礎断面、記号、台形反力分布を定義します。
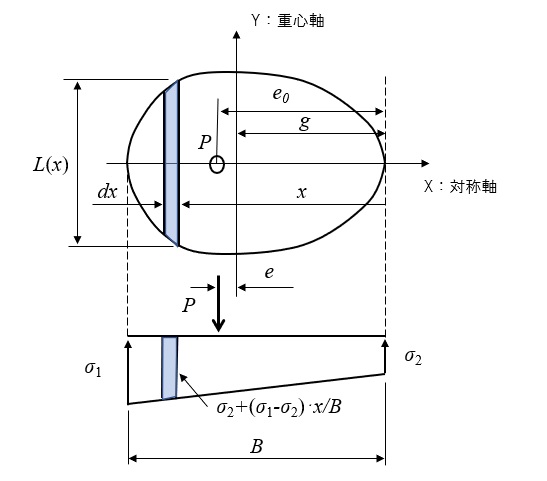
鉛直力\(P\)は反力の総和と釣り合うため、
$$P=\int\big(σ_2+(σ_1-σ_2)\frac{x}{B}\big)L(x)dx\tag{1}$$
モーメントの釣り合いを基礎右端部に対して算定すると、
$$P\cdot e_0=\int\big(σ_2+(σ_1-σ_2)\frac{x}{B}\big)xL(x)dx\tag{2}$$
ここで、断面積\(A\)、対称軸x軸上の右端部に対して算定した断面一次モーメント\(G_x\)、断面二次モーメント\(I_x\)は、
$$A=\int L(x)dx\quad ,\quad G_x=\int xL(x)dx\quad ,\quad I_x=\int x^2L(x)dx$$
これらを式(1)、式(2)に代入すると、
$$P=σ_2A+(σ_1-σ_2)\frac{G_x}{B}\tag{3}$$
$$P\cdot e_0=σ_2G_x+(σ_1-σ_2)\frac{I_x}{B}\tag{4}$$
式(3)と式(4)から\(σ_1\)と\(σ_2\)について解くと、
$$σ_1=\frac{P}{A}+P\frac{(e_0A-G_x)}{(AI_xーG_x^2)}(B-\frac{G_x}{A})\tag{5}$$
$$σ_2=\frac{P}{A}-P\frac{(e_0A-G_x)}{(AI_xーG_x^2)}\frac{G_x}{A}\tag{6}$$
ここで、重心までの距離\(g\)は、
$$g=\frac{G_x}{A}$$
重心位置で算定した断面二次モーメント\(I_G\)と\(Ae\)は、
$$I_G=I_x-g^2A=I_x-(\frac{G_x}{A})^2A$$
$$Ae=A(e_0-g)=A(e_0-\frac{G_x}{A})=e_0A-G_x$$
これらを式(5)と式(6)に代入して整理すると、
$$σ_1=\frac{P}{A}+\frac{Pe}{I_G}(B-g)\tag{7}$$
$$σ_2=\frac{P}{A}-\frac{Pe}{I_G}\tag{8}g$$
なお、\(e’\)は、\(σ_2=0\)の時であるから、式(8)で\(σ_2=0\)とおいて\(e\)について解くと、
$$e’=\frac{I_G}{Ag}\tag{9}$$
基礎の一部分に反力が発生している場合
下図のように基礎断面、記号、三角形反力分布を定義します。
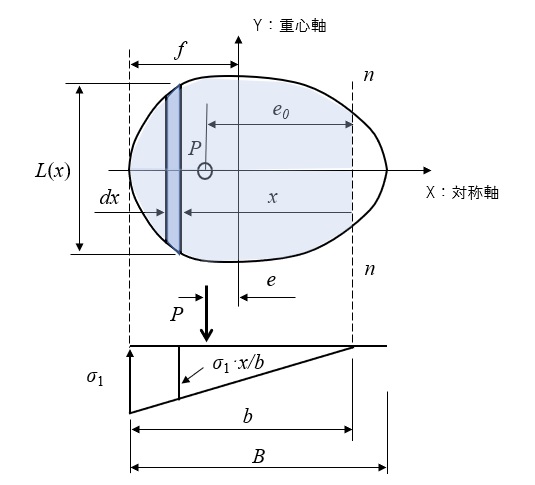
鉛直力の釣り合いと中立軸n-n(反力が0の軸)に対するモーメントの釣り合いから、
$$P=\frac{σ_1}{b}\int xL(x)dx\tag{10}$$
$$P\cdot e_0=\frac{σ_1}{b}\int x^2L(x)dx\tag{11}$$
中立軸n-n(反力が0の軸)に対する反力分布範囲の断面一次モーメントと断面二次モーメントは、
$$G_n=\int xL(x)dx\quad ,\quad I_n=\int x^2L(x)dx$$
したがって、
$$P=\frac{σ_1}{b}G_n\quad ,\quad P\cdot e_0=\frac{σ_1}{b}I_n$$
両辺から\(e_0\)と\(σ_1\)について解くと、
$$e_0=\frac{I_n}{G_n}\tag{12}$$
$$σ_1=\frac{Pb}{G_n}\tag{13}$$
ここで、\(e_0=b-f+e\)を式(12)に代入して、
$$e=\frac{I_n}{G_n}+(f-b)\tag{14}$$
式(12)、式(13)、式(14)が解法の一般解であり、これらを満たす\(b\)と\(σ_1\)を求めればよい。
矩形断面の解
矩形断面の場合は、重心軸が中心に位置するので\(g=B/2\)である。
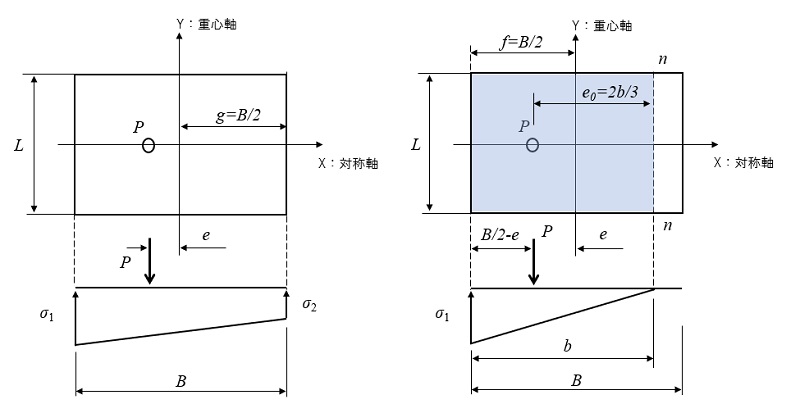
(1)基礎全面に反力が発生している場合
$$A=LB\quad ,\quad g=\frac{B}{2}\quad ,\quad I_G=\frac{LB^3}{12}$$
これらを式(7)、式(8)に代入すると以下のようになり、一般的に知られる解と一致する。
$$σ_1=\frac{P}{LB}(1+\frac{6e}{B})\tag{15}$$
$$σ_2=\frac{P}{LB}(1-\frac{6e}{B})\tag{16}$$
(2)基礎の一部分に反力が発生している場合
$$I_n=\frac{Lb^3}{12}+Lb(\frac{b}{2})^2=\frac{Lb^3}{3}$$
$$G_n=Lb(\frac{b}{2})=\frac{Lb^2}{2}$$
これらを式(14)と式(13)に代入すると以下のようになり、一般的に知られる解と一致する。
$$b=3(\frac{B}{2}-e)\tag{17}$$
$$σ_1=\frac{2P}{3L(B/2-e)}\tag{18}$$
なお、関連ページを以下に示しておきますので、興味がありましたらご覧ください。





コメント