【弾性連続体内の一次元運動】均一な表面力を受ける半無限体（4）

　今回は、半無限弾性体の境界上に作用 $p(t)$ が作用した場合の一次元の方程式を導いていきます。線形化理論を適用した場合の縦波の応力伝播まで定式化します。

変位と応力の運動方程式
粒子速度とエネルギー
静的及び線形化の条件

変位と応力の運動方程式

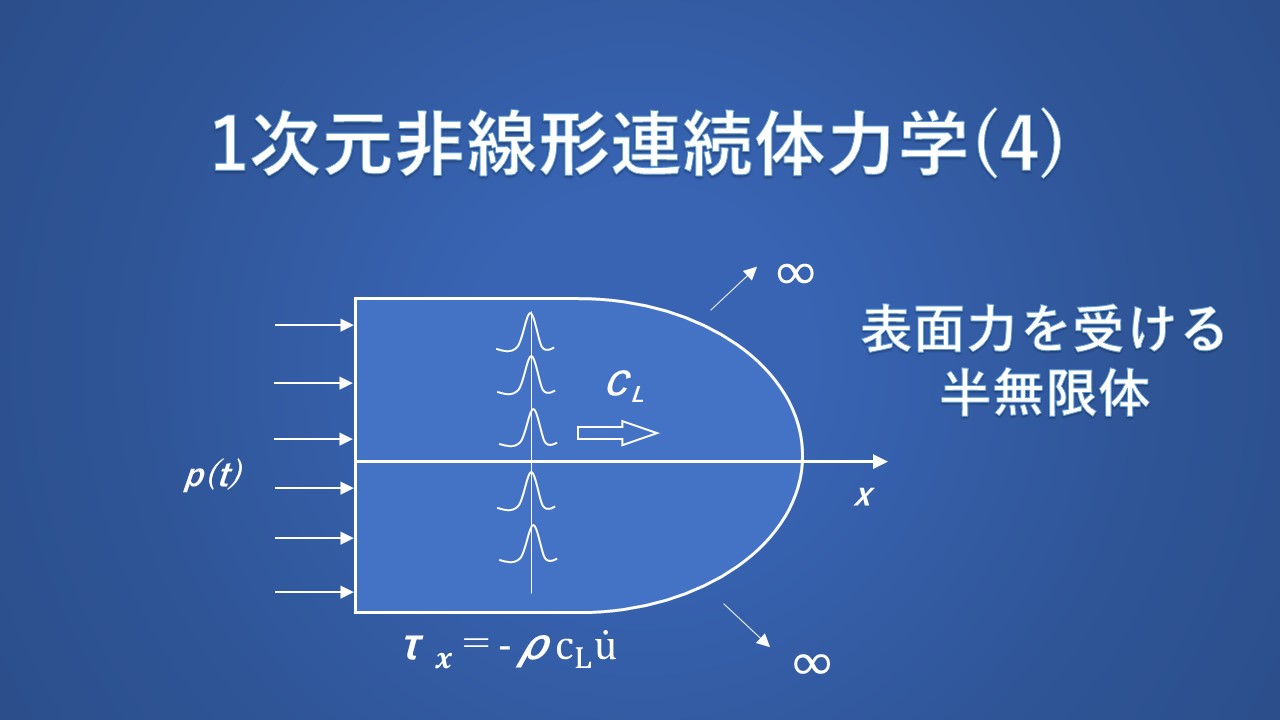
　線形化理論による（過渡）波動伝播の多くの特徴を示す簡単な例として、初期に乱れのない半無限等方均質弾性体に、空間的に均一な表面圧力 $p(t)$ が作用することによって生成される波動を考えます。半無限体が $x≧0$ において定義されるものとします。

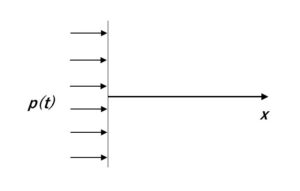
　$x$ 方向の垂直応力を $τ_x(x,t)$ で表すと境界 $x=0$ では、
$$τ_x=-p(t)　ただし、t<0のときp(t)=0\tag{48}$$
同様に $x=0$ において、他の応力成分は存在しません。
　$x$ 軸に平行な平面は明らかに対称面です。結果として横方向への変位は発生せず、半無限空間の動きは、$x$ と $t$ のみの関数である $x$ 方向の変位 $u(x,t)$ によって記述されます。半平面は明らかに 1 次元の変形状態にあり、これまでに定義された方程式が適用されます。したがって、半空間の変形は単一のひずみ成分によって記述されます。

$$ε_x=\frac{\partial u}{\partial x}\tag{49}$$

すなわち半平面は一次元の縦ひずみの状態にあり、式(44)に従えば、応力とひずみは次のような関係にあります。

$$τ_x=(λ+2μ)\frac{\partial u}{\partial x}\tag{50}$$

　一方、変位の運動方程式は次のようになります。

$$\frac{\partial^2 u}{\partial x^2}=\frac{1}{c_L^2}\frac{\partial u}{\partial x}\tag{51}$$

ここで、 $c_L$ は式(47)で定義されたものです。半空間が時間 $t=0$ より前に静止していると仮定すると、式(48)と式(51)はつぎの初期条件によって補足されます。

$$t=0　,　x>0　において、　u=\dot{u}≡0\tag{52}$$

式(51)の一般解は、

$$u(x,t)=f\biggl(t-\frac{x}{c_L}\biggr)+g\biggl(t+\frac{x}{c_L}\biggr)\tag{53}$$

　表面圧力 $p(t)$ が正の $x$ 方向にのみ伝播する波を生成することは直感的に明らかですが、関数 $g(t+x/c_L)$ を先験的に破棄するのではなく、厳密に数学的なアプローチに従います。したがって、式(53)の表記を使用すると初期条件式(52)は、 $x>0$ においてつぎのように書く事ができます。

$$f(-x/c_L)+g(x/c_L)=0\tag{54}$$

$$f'(-x/c_L)+g'(x/c_L)=0\tag{55}$$

ここで、‘　は引数に関する微分を示します。これらの式の解は $x>0$ において、

$$f(-x/c_L)=-g(x/c_L)=A\tag{56}$$

ここで $A$ は定数です。 $t+x/c_L$ は $t≧0$ かつ $x>0$ において常に正であるため、式(53)は初期条件を満足する次式のように書くことが出来ます。

$$u(x,t)=\begin{cases}f(t-x/c_L)-A　for　t>x/c_L\\０　　　　　　　　　for　t<x/c_L\end{cases}\tag{57}$$

この解は、伝播した領域と乱されていない領域を分離する波面が速度 $c_L$ で物体中を伝播することを示しています。 $x=\bar{x}$ にある粒子は、時刻 $t=\bar{t}=\bar{x}/c_L$ まで静止します。
　$x=0$ における境界条件はつぎのようになります。

$$-\frac{λ+2μ}{c_L}f'(t)=-p(t)$$

上式を積分すると $f(t-x/c_L)$ は、

$$f\biggl(t-\frac{x}{c_L}\biggr)=\frac{c_L}{λ+2μ}\int_0^{t-x/c_L}p(s)ds+B\tag{58}$$

ここに、 $B$ は定数です。式(48) によれば、関数 $p(s)$ は $s<0$ の場合にゼロであるため、 $p(s)$ に関する積分は $t<x/c_L$ の場合にゼロとなります。式(58)は式(56)と一致するため $B=A$ となります。変位は、式(58)を使ってつぎのように表されます。

$$u(x,t)=\frac{c_L}{λ+2μ}\int_0^{t-x/c_L}p(s)ds\tag{59}$$

対応する垂直応力 $τ_x(x,t)$ は式(50)から次のように求められます。

$$τ_x=-p\biggl(t-\frac{x}{c_L}\biggr)$$

$τ_y$ および$τ_z$ で示される横方向の垂直応力は、次のように計算できます。

$$τ_y=τ_z=-p\frac{λ}{λ+2μ}\biggl(t-\frac{x}{c_L}\biggr)$$

$u(x,t)$ と $τ_x(x,t)$ の式では、式(48)で示されているように $t<0$ のときは $p(t)≡0$ であることを考慮する必要があります。
　変位と応力の解は、表面圧力が速度 $c_L$ で半無限体内に伝播する変動を生成することを示しています。 $x=\bar{x}$ に位置する粒子は、半無限体内の変動部分と静止部分を分離する波面が到着する時刻 $\bar{t}=\bar{x}/c_L$ まで静止したままになります。 $x=\bar{x}$ における垂直応力は圧縮応力であり、変数 $t=\bar{x}/c_L$ の値に対応する外部圧力の値を持ちます。変位は、変数 $0$ から $t=\bar{x}/c_L$ の間の外部圧力を表す曲線の下の面積に比例します。変位と応力は過渡的な波動を表します。この単純な問題では、応力パルスの形状は媒体中を伝播する際に変化しないことに注意してください。

粒子速度とエネルギー

　式(59)を使用すると、粒子速度 $\dot{u}=\partial u/\partial t$ は次のように計算されます。

$$\dot{u}=\frac{c_L}{λ+2μ}p\biggl(t-\frac{x}{c_L}\biggr)\tag{60}$$

したがって、明らかに、正の $x$ 方向に伝播する波の場合、応力 $τ_x(x,t)$ と粒子速度 $\dot{u}(x,t)$ は次の関係があります（※上記 $τ_x$ と $ｐ$ の関係式と式(47)、式(60)から）。

$$τ_x=-ρc_L\dot{u}\tag{61}$$

応力と粒子速度の比は力学的インピーダンスと呼ばれます。この場合、力学的インピーダンス $ρc_L$ は材料定数です。運動を起こすために必要な応力を測定するため、物質のwave resistance（原文でwave resistanceと書かれていましたが、なじみがない用語ですの原文のまま記載します）と呼ばれることがあります。
　位置 $x$ で $x$ 軸に垂直な単位面積要素を考えると、要素に作用する引張力の瞬間的な仕事率（原文ではpowerと書かれていますが、ここでは仕事率と訳しておきます）は、 $τ_x(x,t)$ と粒子速度 $\dot{u}(x,t)$ のベクトル積になります。この瞬間的な仕事量の比率は単位面積当たりの仕事率として $𝒫$ で表します。

$$𝒫(x,t)=-τ_x\dot{u}\tag{62}$$

マイナス記号が表示されるのは、応力ベクトル (引張力は正) と同じ方向に作用する速度が仕事率の正の値をもたらすためです。式(61)より、

$$𝒫(x,t)=-ρc_L\dot{u}^2\tag{63}$$

仕事率は、単位面積に対して単位時間当たりにエネルギーが伝達される速度を定義します。明らかに、 $𝒫$ は面積要素にわたるエネルギー束を表していますので、総エネルギー密度 $ℋ$ に関連しています。単位体積あたりの総エネルギーは、運動エネルギー密度 $𝒦$ とひずみエネルギー密度 $𝒰$ の合計に等しいため、

$$ℋ=𝒦+𝒰=\frac{1}{2}ρ\dot{u}^2+\frac{1}{2}(λ+2μ)\biggl(\frac{\partial u}{\partial x}\biggr)^2\tag{64}$$

もし、 $x$ を横切る流れよりも多くのエネルギーが点 $x+dx$ を横切って流れる場合、媒質の長さ $dx$ に含まれるエネルギーは減少して、

$$𝒫(x+dx)-𝒫(x)=-dx\frac{\partial ℋ}{\partial t}$$

または、

$$\frac{\partial 𝒫}{\partial x}+\frac{\partial ℋ}{\partial t}=0$$

これはエネルギーの連続方程式です。式(62)と式(64)を代入すると、

$$-\biggl(\frac{\partial τ_x}{\partial x}-ρ\ddot{u}\biggr)\dot{u}-\biggl[τ_x-(λ+2μ)\frac{\partial u}{\partial x}\biggr]\frac{\partial \dot{u}}{\partial x}=0$$

もちろん、同式は式(50)と式(51)から成り立つことが分ります。
　エネルギーは保存されるので、ある時点 $t$ において、表面圧力 $p(t)$ によって加えられた仕事が、半無限空間において伝播した範囲の運動エネルギーとひずみエネルギーの合計に等しく、つまり、

$$\int_0^{t}𝒫(0,t)dt=\int_0^{c_L t}ℋ(x,t)dx\tag{65}$$

左辺は式(63)、式(47)より、

$$\int_0^{t}𝒫(0,t)dt=\frac{c_L}{λ+2μ}\int_0^{t}[p(s)]^2dx$$

式(65)の右辺は式(64)、式(59)より、

$$\int_0^{c_L t}ℋ(x,t)dx=\frac{1}{λ+2μ}\int_0^{c_L t}\biggl[p\biggl(t-\frac{x}{c_L}\biggr)\biggr]^2dx$$

式の変数を変更すると式(65)を簡単に検証できます。