動的弾性問題は、弾性体の運動状態を解析するための問題です。これは、弾性体が時間とともにどのように変形し、応力がどのように発生するかを理解するための重要な手段です。
具体的には、変位、応力、および運動量のフィールドが変化する一連の静的および動的変分原理が提案されています。これらの原理は、弾性体の初期境界値問題の数値解を得るための正規の数値アルゴリズムを提供します。例えば、ハミルトンの原理とその補完原理は、線形弾性の動的問題に対して、提案された変分形式から導き出されます。これらの原理は、弾性体の動的挙動を理解し、予測するための基礎となります。
以上のような理論的な枠組みを用いて、具体的な問題(例えば、特定の形状や材料の弾性体の挙動)を解析することが可能となります。そして、これらの問題を解くことで、弾性体の設計や制御、最適化など、様々な工学的応用が可能となります。
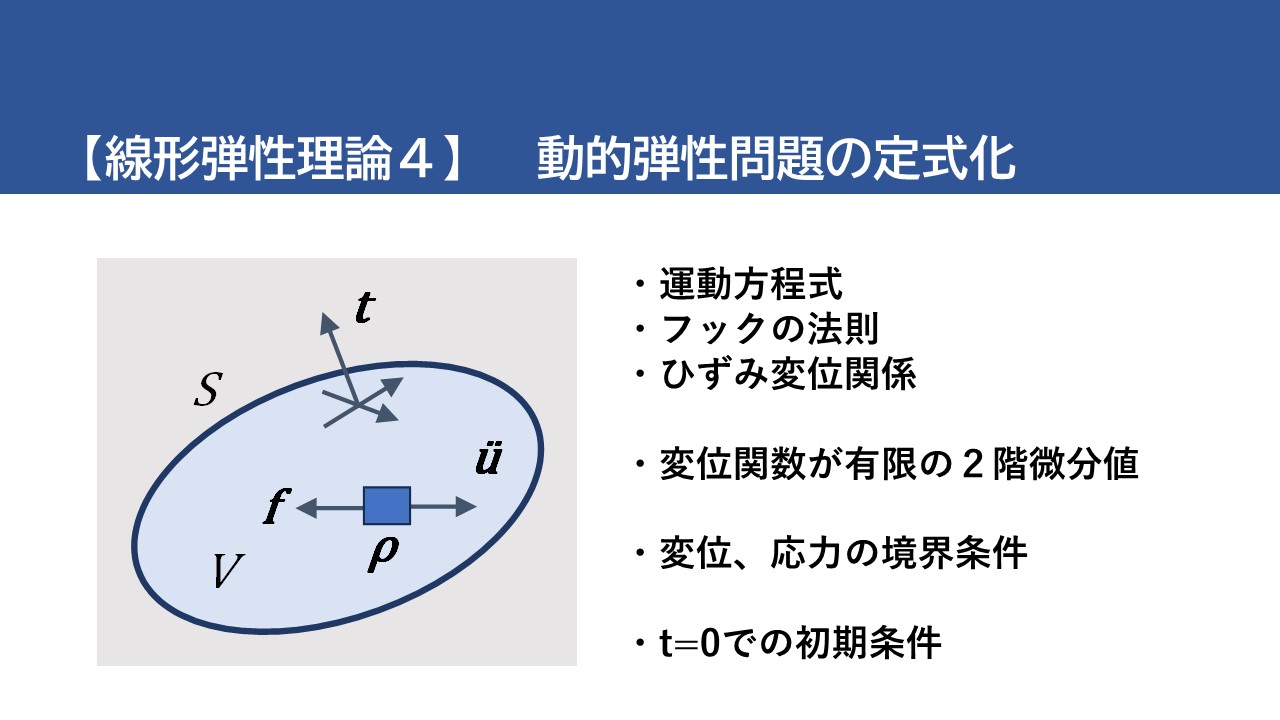
さて、空間内の規則的な領域 \(V\) を占める物体 \(B\) が、内部 \(V\)、閉包 \(\bar{V}\) (\(V+S\)のこと)、境界 \(S\) を持ち、有界(数学的に一定の範囲内に収まること)または無界(制約がないこと)の場合があると考えます。均質等方線形弾性体の支配運動方程式は、応力の運動方程式、フックの法則、およびひずみ変位関係から構成されます。
$$τ_{ij}+ρf_i=ρ\ddot{u}_i\tag{39}$$
$$τ_{ij}=λε_{kk}δ_{ij}+2με_{ij}\tag{40}$$
$$ε_{ij}=\frac{1}{2}(u_{i,j}+u_{j,i})\tag{41}$$
ひずみと変位の関係がフックの法則に代入され、続いて応力の式が応力の運動方程式に代入されると、変位の運動方程式が得られます。
$$μu_{i,jj}+(λ+μ)u_{j,ji}=ρ\ddot{u}_i\tag{42}$$
式(39)~式(42) は、変形していない物体 \(B\) のすべての内部点、つまり領域 \(V\) で満たされなければなりません。一般に、次のようになります。
$$u_i(\mathbf{x},t)∈𝒞^{ 2}(V×T)∩𝒞^{ 1}(\bar{V}×T)\tag{43}$$
$$f_i(\mathbf{x},t)∊𝒞(\bar{V}×T)\tag{44}$$
ここで、\(T\) は任意の時間間隔です。\(V×T\) は、弾性体の動的問題において、空間 \(V\) と時間 \(T\) の直積を表しています。直積は、2つの集合のすべての組み合わせを考えることを意味します。\(𝒞(R)\) によって定義される関数の集合は、部分集合 \(R\) 上で定義され、連続するテンソル値関数です。正の整数 \(n\) に対して、\(𝒞^n(R)\) という表記は、Rの内部に存在し、\(n\) 次までの偏微分を持つ \(𝒞(R)\) 内のすべての関数を表すために使用されます。これは、これらの関数が微分可能であるだけでなく、その導関数もクラス \(𝒞(R)\) に属することを意味します。変位が滑らかさの要件式(43)を満たさない場合 、別々の関係は不連続性によって満たされなければなりません。
変形していない物体の表面 \(S\) では、境界条件を規定する必要があります。次の境界条件が最も一般的です。
(i) 変位境界条件: 3 つの変位成分 \(u_i\) が境界上に存在します。
(ⅱ) 応力境界条件: 3 つの応力成分 \(t_i\) は単位法線ベクトル \(\mathbf{n}\) をもつ境界で規定されます。コーシーの公式によって、
$$t_i=τ_{ji}n_j\tag{45}$$
このケースは、実際には応力テンソルの 3 つの成分の条件に対応します。
(ⅲ) 境界の部分 \(S_1\) には変位境界条件が、残りの部分 \(S-S_1\) にはトラクション境界条件が適用されます。
物体の境界では他の条件も可能です。
動的弾性問題の定式化を完成させるために、領域 \(V\) において時間 \(t=0\) での初期条件を定義します。
$$u_i(\mathbf{x},0)=u^0_i(\mathbf{x})$$
$$\dot{u}_i(\mathbf{x},0^+)=v^0_i(\mathbf{x})$$
以上、今回は大雑把な動的弾性問題の定式化について示しました。


コメント