【衝撃載荷による一様成層地盤の波動伝播特性６】解析パラメータの設定と解の精度

　今回はディスク載荷による遷移応答解を求める際の解析パラメータの設定と解の精度について検討を行います。引き続きExcel_2021のVBAで逆ハンケル変換を行っています。
　観測点は地表面上に採り、その変位 $U_{ij}$ は $j$ 方向載荷 $(j=x,z)$ に対する $i$ 方向のフーリエ振幅 $(i=r,θ,z)$ であることを示しています。衝撃載荷モデルとして、解析時間刻み $Δt$ 間に強度１kNのディスク載荷を作用させました。

基本長の設定

　本解析法で用いている離散化波数法は、有限区間内 $0≦x≦L$ で波動を定義し、そのフーリエ級数和として解が表現される。ここに、$L$ を基本長と呼び、これは解の精度に大きな影響を与えるパラメータである。離散化波数の下限値は、$ξ=2π/L$ として定義され、基本長に制約を受ける。また、フーリエ級数の性質から、基本長が十分でない場合には、$x=L$ 点からの反射波が現れる。従って、解にこれらの反射波の影響を与えないように十分な基本長 $L$ を設定しなければならない。$x=L$ 点からの反射波の影響は、最も速いP波について考えればよい。載荷点で発生したP波が $x=L$ 点に到達し、観測点に反射してくる時間は、載荷点までの距離を $r$ として $t=(2L-r)/V_{p}$ と表わされる。

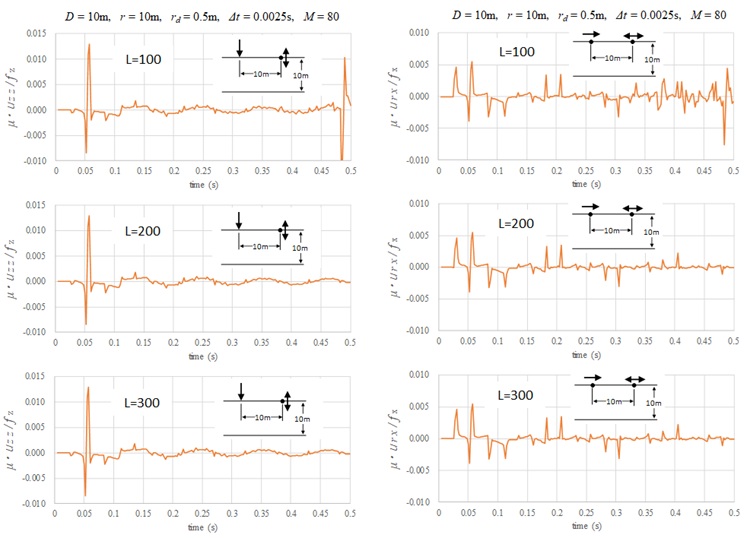
　上図は、地表面に衝撃ディスク載荷が作用した場合の地表面変位解であり、$L=100m$ , $200m$ , $300m$ とした場合を比較している。載荷および変位方向と解析パラメータは図中に示したが、地盤定数は、$V_{s}＝200m/s$ , $ν=0.3$ である。波数の打ち切り項数を $K=2L$、モードの打ち切り次数を $M=80$ とした。なお、変位解がP波到達までの因果性を満足していることから、これら解析パラメータの設定範囲が十分であったと言える。同図では $L=100m$ の場合に0.48ｓで反射波が現れているが、0.3ｓ程度から既に基本長の影響が見られるが、反射波の影響が現れる時刻までの変位は、基本長の長さによらず十分な精度を有している。また、$L=200m、300m$ の場合には反射波の影響は見られず、同様な変位解となっている。従って、離散化波数の下限値については、 $L=100m$ の場合を参考に、$ξD≦0.2π$ 程度が目安となる。また、解析時間 $t$ 内に $x=L$ 点からの影響が解に現れないような基本長は、$L>tV_{p}$ とすれば十分である。以上より、基本長の設定は次式によれば良い。

$$L= max(tV_{p}，10D)\tag{55}$$

離散化波数の打ち切り項数とモードの打ち切り次数

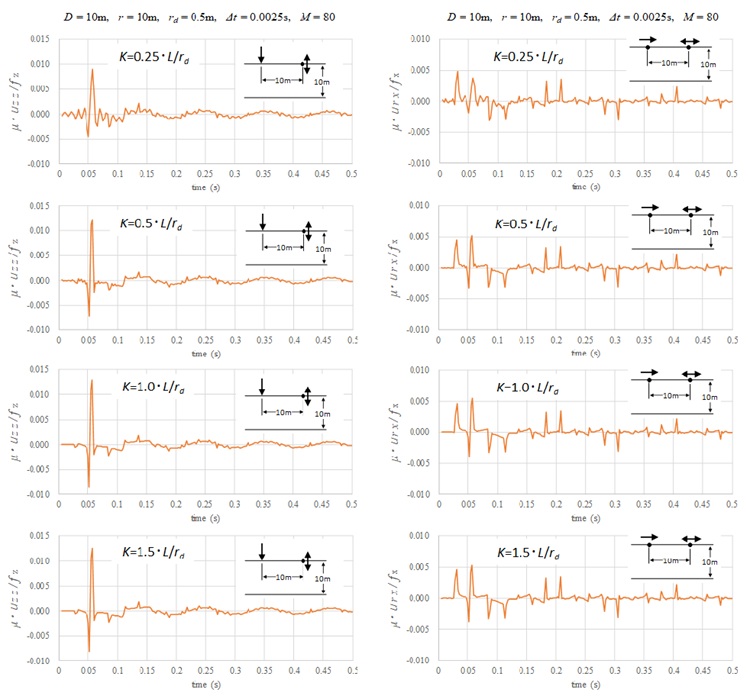
　離散化波数の打ち切り項数は、衝撃載荷による一様成層地盤の波動伝播特性５の考察で述べたように、ディスク半径による伝達関数の波数域によって設定することができる。波数領域のディスク載荷の表現式に含まれる $J_{1}(ξr_{d})/ξr_{d}$ の性質から、波数の上限値として $ξr_{d}=2π$ が目安となると考えられる。このとき、離散化波数の打ち切り項数は $K=L/r_{d}$ と表現される。下図は $K$ を $L/r_{d}$ の0.25倍、0.5倍、1.0倍、1.5倍とした場合の変位解であるが、 $K=L/r_{d}$ とすれば問題の無い精度であることが分かる。

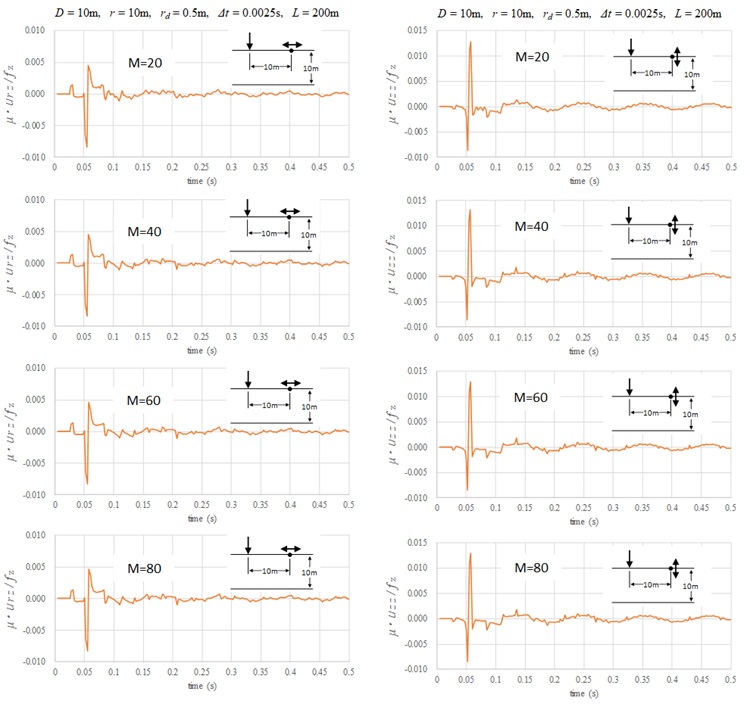
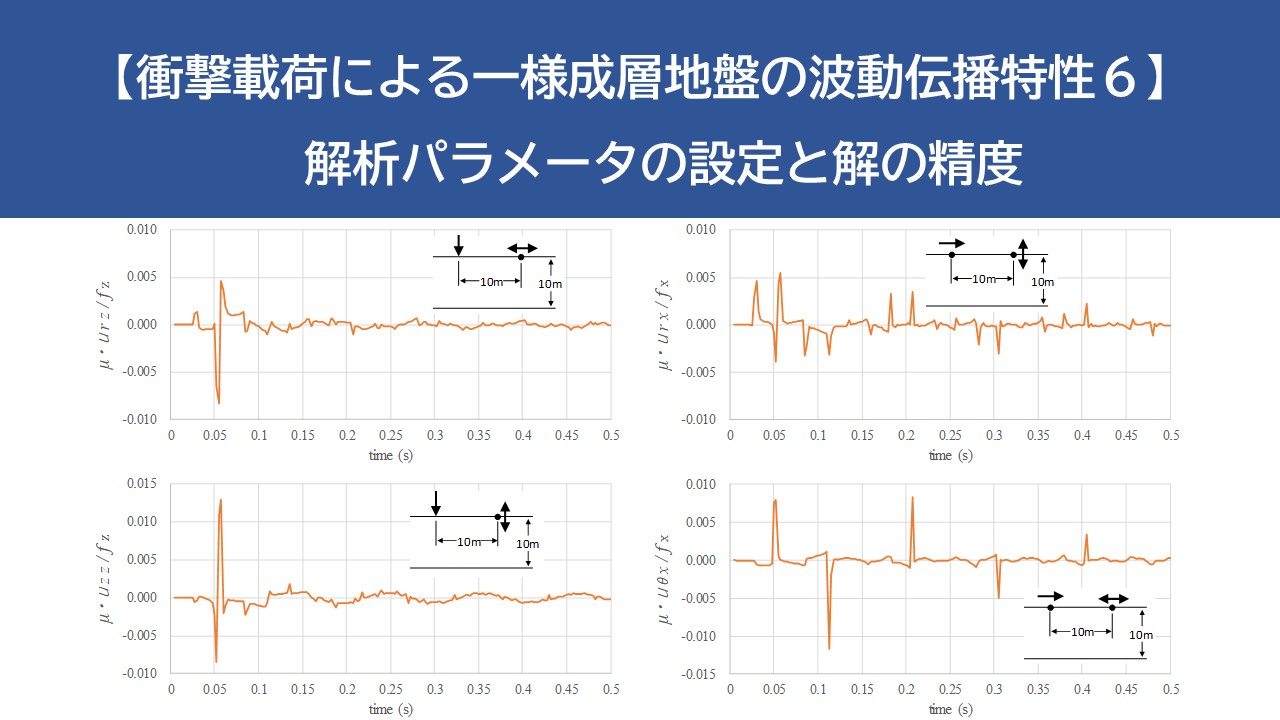
　つぎに、モードの打ち切り次数について検討を行う。本解析法では、ラプラス領域解を留数定理より解析的に時間領域に逆変換し、それぞれのモードの重ね合わせとして解を得る。従って、各モードの解は因果性を満足するための必要条件を満足しているものの、因果性を満足した精度の良い時刻歴解を得るかどうかは、モードの打ち切り次数によって決まる。下図は地表面載荷による地表面応答についてモード次数による解の精度を示したものである。地盤定数は、$V_{s}＝200m/s$ , $ν=0.3$ であり、載荷および変位方向と解析パラメータは図中に示した。これによると、収束性は良く、20次モードまでの採用でもほぼ応答を近似でき、さらに40次モードまでを採用することで十分な精度が得られることが分かる。これは載荷点から観測点までの距離を10ｍとしたことと、地表面載荷では低次モードが卓越することによる。

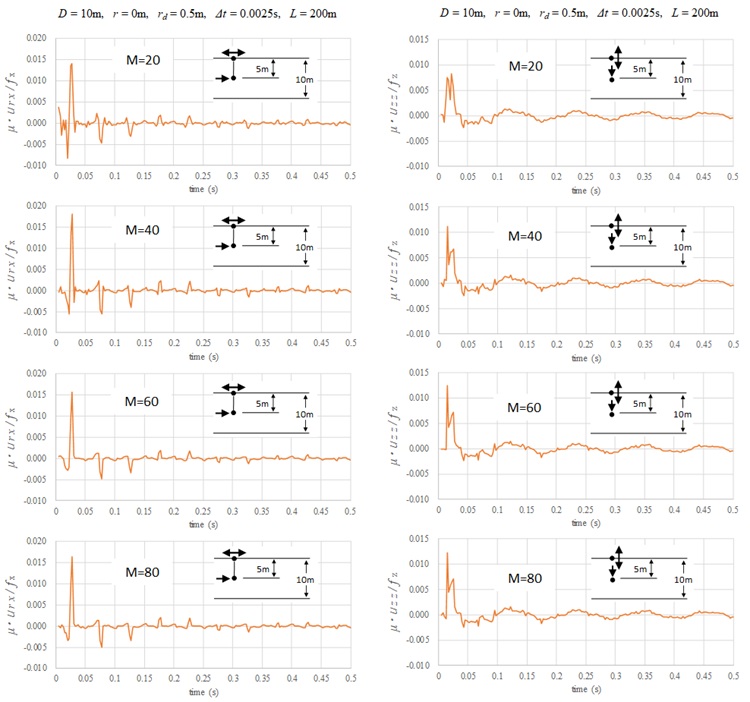
　さらに、高次モードの寄与が高い、地中載荷による載荷点直上に位置する地表面での変位解について検討した結果を下図に示す。解析モデルおよび解析パラメータは、上図と同じである。この場合には収束性が悪く、60次モードまでを採用することによって、因果性を満足する解が得られている。この場合の60次モードは、波数の小さい領域で現れる地盤振動に直せば約200Hzとなり、これは衝撃載荷が作用する時間の逆数 $1/2Δt$ に一致する。従って、ディスク半径がここで用いた0.5m程度あるいはそれ以上であれば、 $1/2Δt$ Hzまでの地盤振動を採ることが目安となる。いま、当該解析対象モデルは剛基盤上の一様成層地盤であり、ポアソン比が同じであれば層厚 $D$ および $V_{s}$ によって無次元化表示が可能である。そこで、ポアソン比0.3の地盤における固有振動数を目安としてモードの打ち切り次数を次式により設定することを提案する。

$$M= 4D/(V_{s}Δt)\tag{56}$$

層厚による応答特性

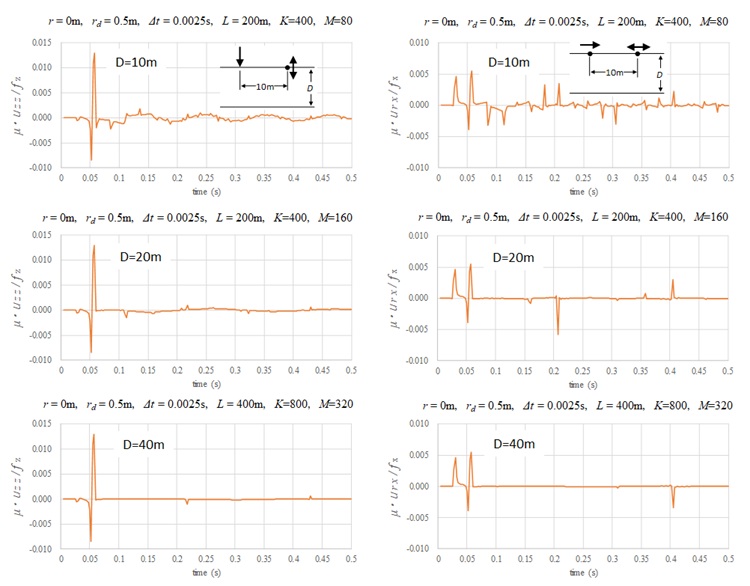
　層厚を $D=10m$ , $D=20m$ , $D=40m$ としたケースで、地表面載荷時の地表面応答傾向を調べてみた。0.05s当たりに見られる応答は $V_{s}$ 波あるいは $V_{r}$ 波の直達波であり、その約半分の時間で見られる応答は $V_{p}$ 波の直達波である。それぞれのケースでその後に現れる振動はAiry相の1次モードの周期を示し、層厚が厚いほど振幅が小さくなる。また、水平載荷の水平変位に顕著であるように、実体波の反射波が層厚に応じた周期で繰り返し現れる。
　なお、各解析パラメータを図中に示した。各層厚に対して十分な精度の応答変位が得られており、先述した解析パラメータの設定方法が妥当であることが分かる。