Excelのデータ分析ツールにはフーリエ変換、フーリエ逆変換がありますが、データ数4,096の制約があります。昨今、地震波データとして160秒以上の継続時間を扱うことが多いため、データ数に制約がないFFTをVBAで作ってみることにしました。
Excelには複素数の型がない
ExcelにはFortranのようなcomplexの型が無いようです。
実部、虚部に分けて実数で計算していけば問題ないのですが、今後も複素数を利用した計算を行う可能性があるかもしれません。そのため、型と簡単な複素数の関数を定義しました。
定義式は、”あもんノート~理論物理学のまとめ~”から、数値計算 for VBAを使用させていただきました。
Option Explicit
Dim ND, N, I, J, K, M, Kmax, Istep, IND As Long
Dim dt, pi As Double
Dim X(16384) As complex
'=== 複素数と複素行列の型 ===
Type complex
re As Double '実部
im As Double '虚部
End Type
'=== 複素数の実表示 ===
Function cn(a As Double, b As Double) As complex
cn.re = a
cn.im = b
End Function
'複素数の絶対値
Function cabs(a As complex) As Double
cabs = (a.re * a.re + a.im * a.im) ^ 0.5
End Function
'=== 複素数の和 ===
Function csum(a As complex, b As complex) As complex
csum.re = a.re + b.re
csum.im = a.im + b.im
End Function
'=== 複素数の差 ===
Function cdif(a As complex, b As complex) As complex
cdif.re = a.re - b.re
cdif.im = a.im - b.im
End Function
'=== 複素数の積 ===
Function cpro(a As complex, b As complex) As complex
cpro.re = a.re * b.re - a.im * b.im
cpro.im = a.re * b.im + a.im * b.re
End Function
'=== 複素数の指数関数 ===
Function cexp(a As complex) As complex
cexp.re = Exp(a.re) * Cos(a.im)
cexp.im = Exp(a.re) * Sin(a.im)
End FunctionFFTを作成
高速フーリエ変換FFT、IFFTは、株式会社大崎総合研究所が公開しているプログラムソース”プログラムの公開について”(「新・地震動のスペクトル解析入門(鹿島出版1994年)」に掲載)をVBAに書き換えました。
'=== 高速フーリエ変換 Ind=-1:FFT,Ind=1:IFFT ===
Sub fast(IND)
Dim Temp As complex
Dim Theta As complex
J = 1
For I = 1 To N
If I < J Then
Temp = X(J)
X(J) = X(I)
X(I) = Temp
End If
M = N / 2
L1:
If J > M Then
J = J - M
M = M / 2
If M >= 2 Then
GoTo L1
End If
End If
J = J + M
Next I
Kmax = 1
L2:
If (Kmax >= N) Then
Exit Sub
End If
Istep = Kmax * 2
For K = 1 To Kmax
Theta = cn(0#, pi * IND * (K - 1) / Kmax)
For I = K To N Step Istep
J = I + Kmax
Temp = cpro(X(J), cexp(Theta))
X(J) = cdif(X(I), Temp)
X(I) = csum(X(I), Temp)
Next I
Next K
Kmax = Istep
GoTo L2
End SubFFT→IFFTで試算
時刻歴の離散データからFFTを使って振動数成分に変換し、さらにIFFTにて時刻歴データに戻してみます。
離散データはつぎの式において、A1=1.0,A2=0.5,A3=0.8,f1=2.0Hz,f2=7.0Hz,f3=10.0Hzとし、データ数512,時間刻みΔt=0.01sとしました。
X(t)=A1・sin(2π・f1・t)+A2・sin(2π・f2・t)+A3・sin(2π・f3・t)
Excelシート上に離散データt(s),X(t)を作成し、フーリエ変換の結果をG~J列に、フーリエ逆変換の結果をK,L列に出力しています。
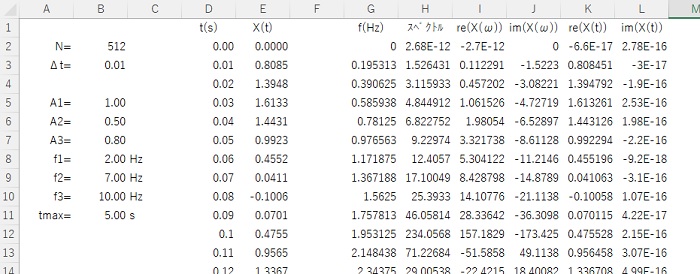
この計算のプロシージャは、以下の通りです。
Sub フーリエ変換()
pi = 3.14159265359
ND = Range("B2").Value
dt = Range("B3").Value
For I = 1 To 14
Kmax = 2 ^ I
If ND <= Kmax Then
N = Kmax
Exit For
End If
Next I
If ND > Kmax Then
MsgBox "データ数>16384 計算を終了します。", vbOKOnly
End
End If
For I = 1 To ND
X(I) = cn(Cells(I + 1, 5), 0#)
Next I
If N > ND Then
For I = ND + 1 To N
X(I) = cn(0#, 0#)
Next I
End If
Call fast(-1)
For I = 1 To N / 2
Cells(I + 1, 7) = (I - 1) / N / dt
Cells(I + 1, 8) = cabs(X(I))
Cells(I + 1, 9) = X(I).re
Cells(I + 1, 10) = X(I).im
Next I
Call fast(1)
For I = 1 To N
Cells(I + 1, 11) = X(I).re / N
Cells(I + 1, 12) = X(I).im / N
Next I
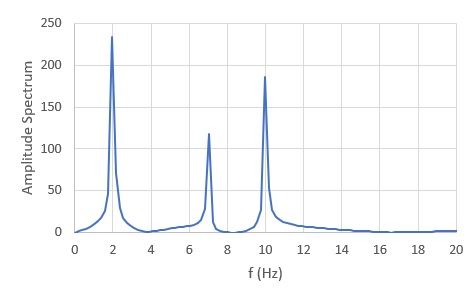
End Subフーリエスペクトルはつぎのようで、f1=2.0Hz,f2=7.0Hz,f3=10.0Hzで卓越しています。
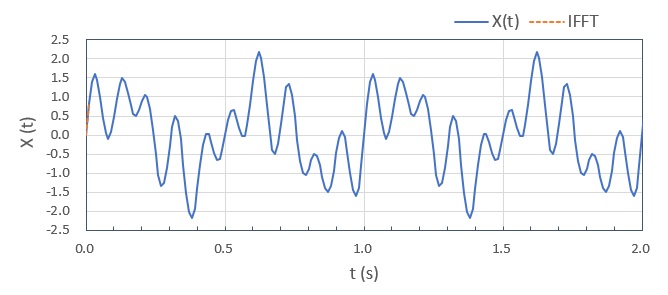
フーリエ逆変換の結果は下図のようであり、ほぼ合致しました。
まとめ
高速フーリエ変換をExcelVBAで作成し、実施してみました。Fortranやpython等を用いれば何でもないFFTですが、手軽にExcelを使って分析したい場合があり、FFTのExcelシートがほしいと思っていたところでした。
Excelにはcomplexの型が無いことから、complexの型の定義や関数を定義する必要があること、データ分析ツールにはデータ数4,096の制限があることなど、今回も勉強になる事が多くありました。
なお、たぶんプログラム内容はOKでは無いかと思いますが、細かくチェックしていません。したがいまして、公開しているプログラム内容については、一切の責任を負いません。使用を目的としてコピー等をされる場合には、個人の責任においてご利用ください。


コメント