今回は一次元縦応力波についての方程式です。一次元縦ひずみ波と比較して考えます。
一次元縦応力波
一次元縦ひずみの波は、純粋に縦方向の擾乱の唯一の種類の波動ではありません。 2 番目のタイプは、1 次元応力の波動によって証明され、長手方向の法線応力、たとえば \(τ_x\) ( \(x\) と \(t\) のみの関数) が 1 つの非消失応力成分になり、他のすべての応力成分は消滅します。
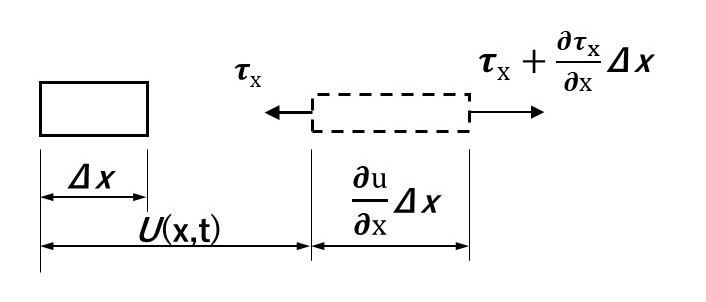
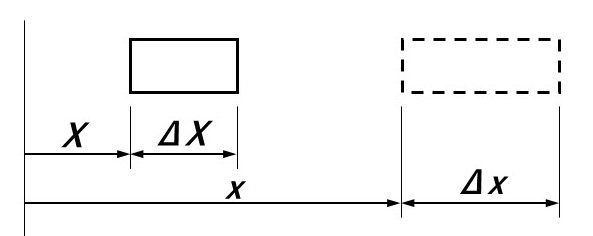
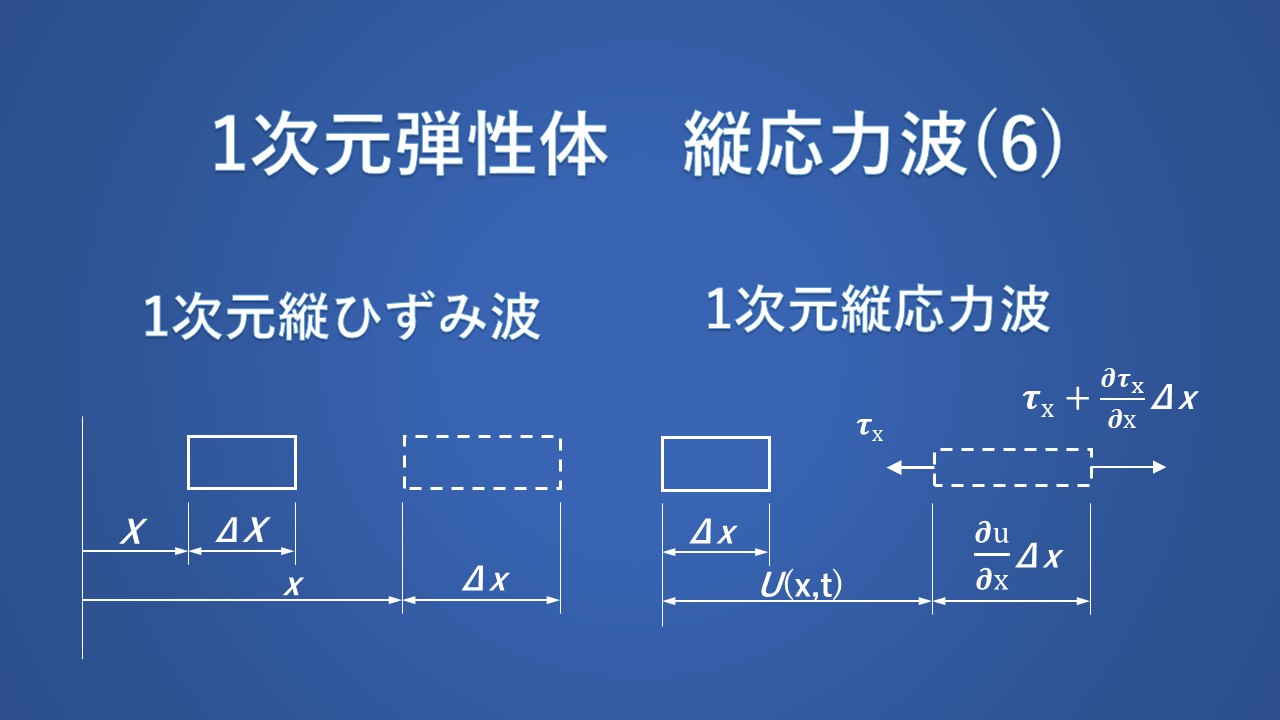
一次元応力による要素の変形を図1に示します。以前スケッチした図2の変形との違いは、一次元応力では要素が横方向に変形することを妨げられないことです。実際、図1に示すように、要素に張力がかかると断面積が減少します。 1 次元応力の場合、 \(τ_x\) と \(ε_x\) は次のように関係付けられます。
$$τ_x=Eε_x\tag{69}$$
ここで、\(E\) はヤング係数です。要素の運動方程式を書くと、
$$\frac{\partial τ_x}{\partial x}=ρ\frac{\partial^2 u}{\partial t^2}\tag{70}$$
式(69)を上式に代入して、
$$\frac{\partial^2 u}{\partial x^2}=\frac{1}{c_b^2}\frac{\partial^2 u}{\partial t^2}\tag{71}$$
ここで、
$$c_b^2=\frac{E}{ρ}\tag{72}$$
応力の一次元状態にある波は、細い棒の波動に近似します。 速度 \(c_b\) は通常、棒速度と呼ばれます。半無限の細い棒 \((x≧0)\) が \(x=0\) で圧力 \(p(t)\) にさらされると、結果として生じる応力波は次のようになります。
$$τ_x=-p\biggl(t-\frac{x}{c_b}\biggr)\tag{73}$$
式(73)は非常に細いロッドにのみ有効な近似解であることを強調しておく必要があります。ロッドが非常に太い場合、変形は一次元のひずみの状態に近づくことが予想されます。多くの場合、ロッドは非常に薄くも厚くもなく、そのためどちらの近似も満足のいくものではなく、フィールド変数の 2 次元または 3 次元の変動を可能にするより正確な処理が必要です。ただし、一次元応力の近似は一般に非常に満足のいくものであることがわかります。
今回は短い内容でしたが、2次元問題の平面ひずみと平面応力と同じく、境界条件の考え方とも言えそうですね。次回は調和波について勉強します。

コメント