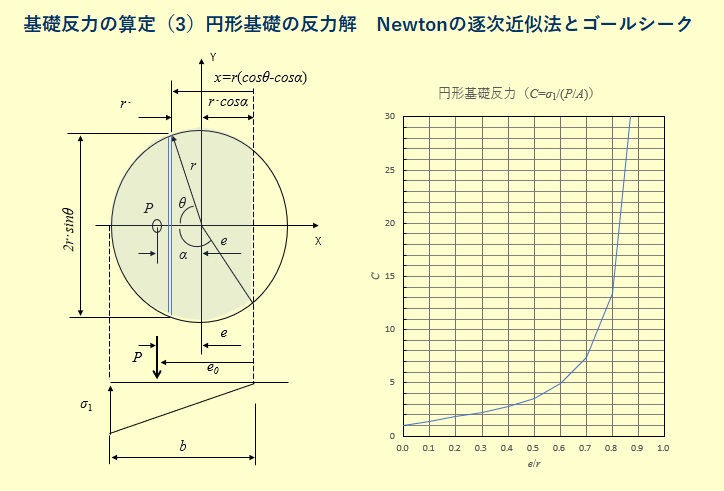
円形基礎反力の計算では、三角形分布となる時、基礎反力が分布する範囲の角度\(α\)を繰り返し計算により求める必要があります。ここでは、Newtonの逐次近似法で求める場合とゴールシークでExcelシート上で解を求める方法について説明します。ゴールシークは条件式と変数セルを指定して、Excel内で条件を満足する解を求める方法ですが、手軽に解を求められるために実務ではよく利用されています。これら解法の精度についても調べていますので参考になれば幸いです。
Newtonの逐次近似法の適用
基礎反力の計算(2)の式(29)より、両辺の差をとって、
$$Z(x)=\frac{\displaystyle \frac{x}{4}-sinx・cosx\big(\frac{5}{12}-\frac{(cosx)^2}{6}\big)}{\displaystyle \frac{sinx}{3}\big(2+(cosx)^2\big)-x・cosx}-\frac{e}{r}\tag{34}$$
と定義すれば、基礎反力が分布する範囲の角度\(α\)は上式の\(Z(x)\)がゼロになるときの\(x\)の値です。
さて、\(Z(x)\)がゼロとなる\(x\)を求めるために、Newtonの逐次近似法を用います。Newtonの逐次近似法は、\(x_1\)における勾配\(Z'(x_1)\)を求めて、この勾配の直線を\(Z(x_1)\)の点から引いてX軸と交わる点(\(Z(x)=0\))のX座標を\(x_2\)とすると、
$$Z’(x_1)=\frac{Z(x_1)}{x_2- x_1}$$
$$∴x_2=x_1-\frac{Z(x_1)}{Z’(x_1)}\tag{35}$$
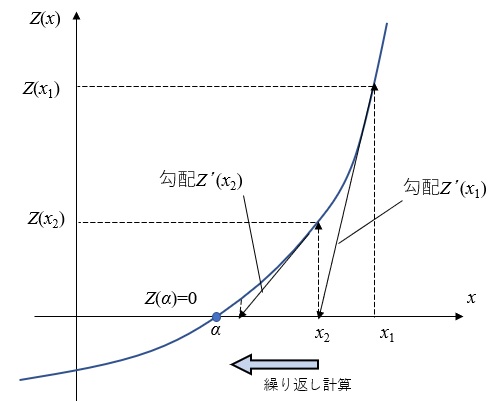
よって、式(35)に\(x_1\)の値を入力して得られた\(x_2\)を\(x_1\)とおいて計算します。これを繰り返し、次式で定義される誤差をε以下になるまで実施します。得られた解\(x_2=α\)を基礎反力の計算(2)の式(30)、式(31)に代入することで、反力\(σ_1\)と反力分布幅\(b\)が求まります。なお、\(0<x≦2π\)であり、ここでは初期値として\(x=π\)とします。
$$|1-\frac{X_1}{X_2}|<ε$$
ここで、
$$f(x)=\frac{x}{4}-sinx・cosx\big(\frac{5}{12}-\frac{(cosx)^2}{6}\big)\tag{36}$$
$$g(x)=\frac{sinx}{3}\big(2+(cosx)^2\big)-x・cosx\tag{37}$$
とおくと、
$$Z(x)=\frac{f(x)}{g(x)}-\frac{e}{r}\tag{38}$$
同式を\(x\)で1回微分すると、
$$Z’ (x)=\frac{f'(x)g(x)-f(x)g'(x)}{g(x)^2}\tag{39}$$
$$f'(x)=\frac{1}{4}-\big((cosx)^2-(sinx)^2\big)\big(\frac{5}{12}-\frac{(cosx)^2}{6}\big)-\frac{(cosx)^2・(sinx)^2}{3}$$
$$=\frac{2(sinx)^4}{3}\tag{40}$$
$$g’ (x)=\frac{1}{3}\big(cosx(2+(cosx)^2)+sinx(-2sin・・cosx)\big)-cosx+x・sinx$$
$$=sinx(x-cos・sinx)\tag{41}$$
ゴールシークによるαの算定
Excelのゴールシークを用いれば、式(34)がゼロになるときの値を\(α\)直接求めることが出来ます。ゴールシークは、変数、条件式と目標値を設定して繰り返し計算により解を求めるが、変数の変動範囲の設定や収束誤差等の判定をどのように設定されているかが分かりません。収束しないケースや変動範囲を超えた解を出力される場合もたまにあります。しかし、便利な機能であるため、実務ではゴールシークを用いている方も多いと思います。
さて、Excelシート上に鉛直荷重合力、重心からの作用距離、基礎の直径を入力しておき、入力値をセル$J$11に、その値から式(34)の計算式をセル$J$12に入力して誤差e/rとしておきます。また、\(d’\)と\(σ\)は基礎反力の計算(2)の式(30)、式(31)よりExcel内で計算式を入力しておきます。
ゴールシークは、データ ⇒ What-If分析 ⇒ ゴールシーク(G)をクリックすると、
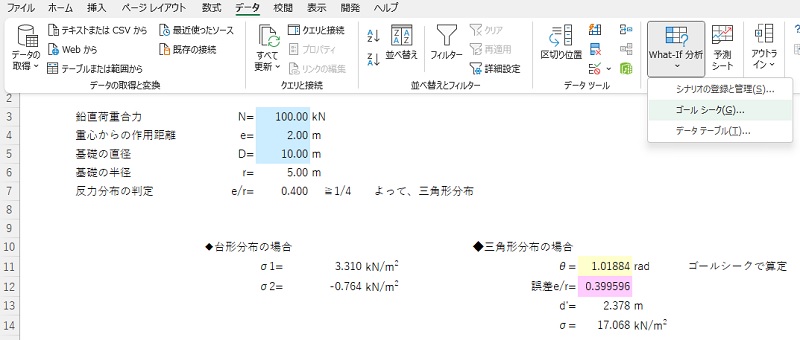
下図のように入力窓が開きます。誤差を数式計算したセルを数式入力セル(E)に、その目標値に0を入力、変数を変化させるセル(C)に指定してOKをクリックすると、

条件に合致した結果が変化させるセル(C)として指定したセルに出力されます。

Newtonの逐次近似法とゴールシークの比較
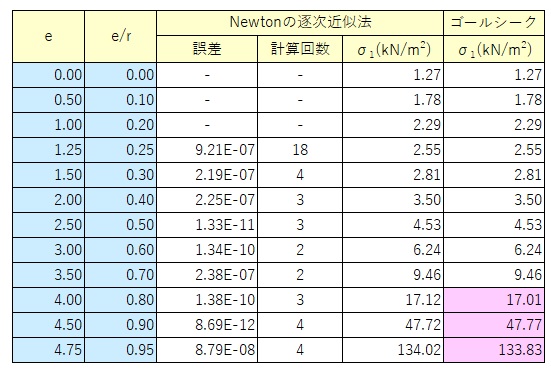
Newtonの逐次近似法で求めた解とゴールシークで求めた解を比較して下表に示します。偏心量\(e\)が半径に近づいてくると、小数点1~2桁の値に差が現れるが、大きく偏心していない状態では、ゴールシークでも十分な精度で解が得られていることが分かる。
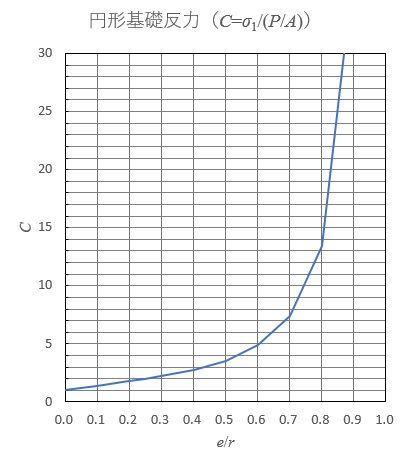
なお、Newtonの逐次近似法で求めた\(C\)を\(\frac{e}{r}\)に対してプロットしたものを下図に示します。
参考:Newtonの逐次近似法のプロシージャ
参考に実際の計算に用いたExcelシートとNewtonの逐次近似法のプロシージャを示します。Excelシート上には、青色セル内に入力値を入力して計算実行ボタンを押すと、反力分布の判定と出力される出力されるように作成しました。計算実行ボタン(コマンドボタン)の設定は、VBAでコマンドボタンから鋼管杭の断面諸元計算のプロシージャを実行する!に簡単に説明していますので、必要であればご覧ください。
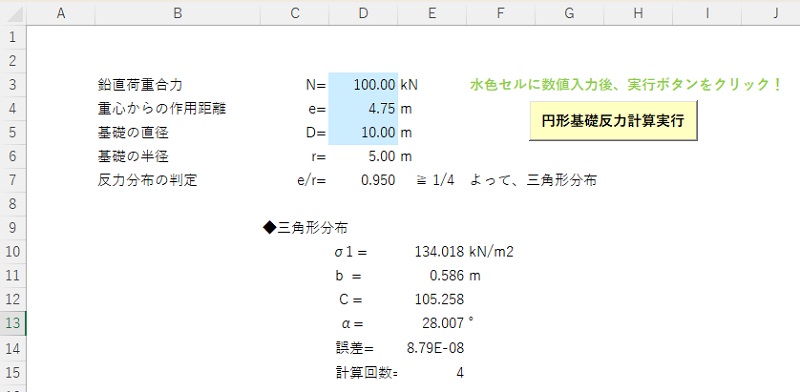
以下に今回の計算に用いたプロシージャのコピーを示します。
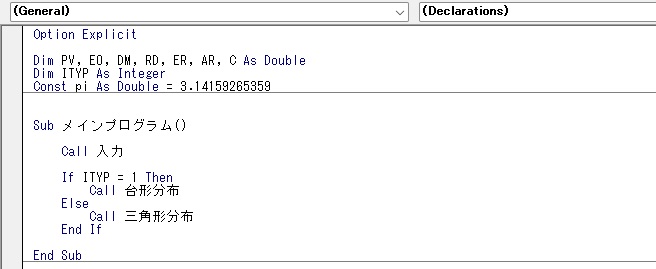

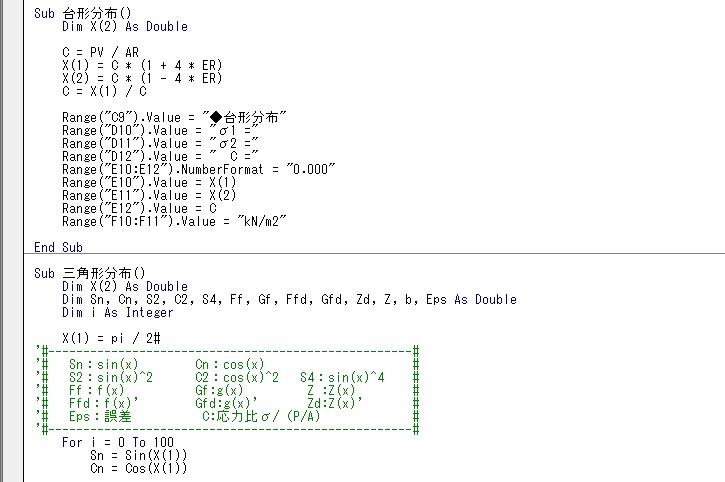






コメント