衝撃載荷による一様成層地盤の波動伝播特性について示してきましたが、今回は最終回として遷移応答特性について示します。
地表面衝撃載荷による地表面変位応答
\(ν=0.3\) の場合の地表面変位応答
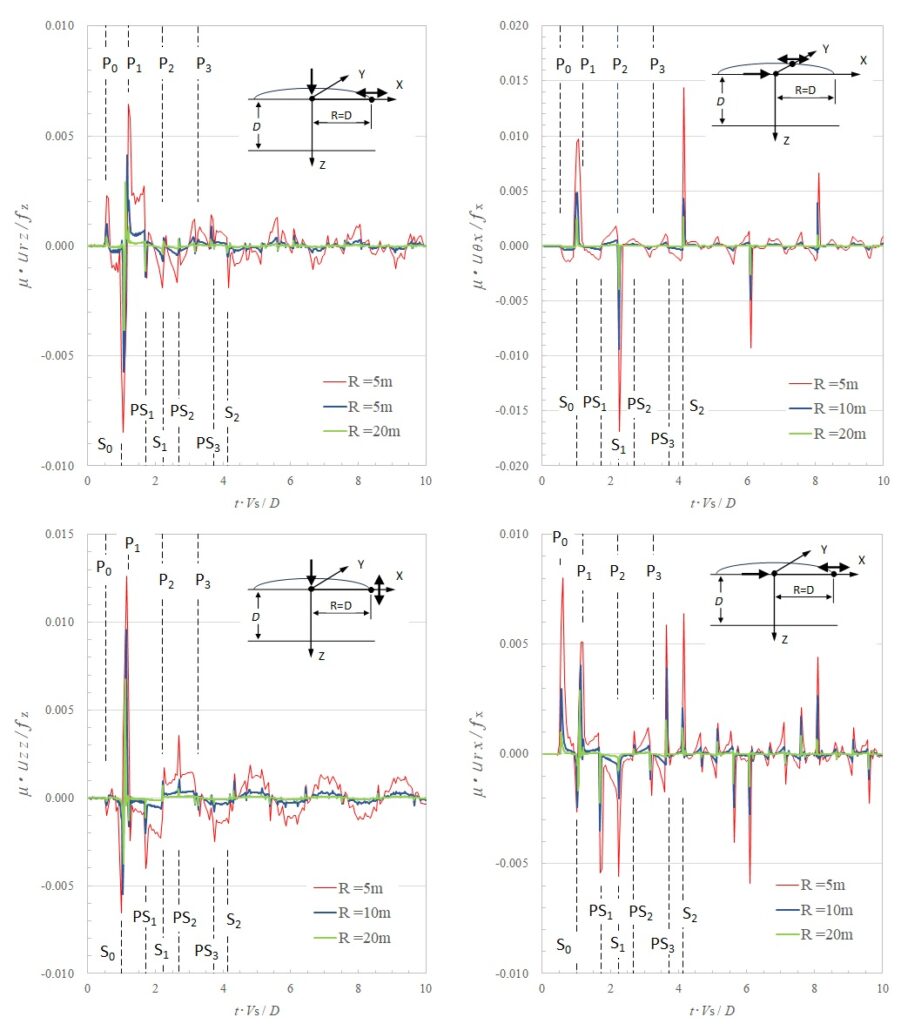
下図は、\(V_{s}=200m/s\) , \(V_{p}=374.17m/s\) , \(ν=0.3\) の地盤に、ディスク半径 \(r_{d}=0.5m\) 、 \(Δt=0.00125s\) の地表面衝撃載荷による地表面での時刻歴変位応答であり、層厚5m,10m,20mの場合を比較して示した。載荷点から観測点までの距離はそれぞれの層厚を採っており、幾何学的に相似な位置としている。従って、時間に関しては層厚 \(D\) とせん断波速度 \(V_{s}\) による無次元化表示によって、同位相の時刻歴変位応答として捉えることができる。
また、各図中に示す \(S_{i}\), \(P_{i}\), \(PS_{i}\) はそれぞれS波、P波、S波およびP波からなる波動の観測点への到達時間を表わし、添字 \(i\) は基盤での反射回数を示す。つまり、\(S_{0}\) はS波の直達波を、\(P_{0}\) はP波の直達波を表わし、\(S_{i}\) および \(P_{i}\) はS波あるいはP波が基盤で \(i\) 回反射した後に観測点に到達した時刻を表わす。\(PS_{i}\) はP波が反射を繰り返す内に発生したS波が観測点に到達する時刻である。これらの到達時間は、Snellの法則から計算された値である。
下図からは、解析解のピーク時間とSnellの法則から求められた波動の時刻歴時刻が非常に良い精度で合致していることが確認できる。鉛直方向載荷による変位は、これらの反射波とRayleigh波の到達波およびその後に現れる地盤振動からなる事が分かる。それらの振幅に注目すると、各モデルの相似比を \(l\) とすると、Rayleigh波の到達波では \(1/\sqrt{l}\)に、 S波およびP波の反射波は \(1/l\)に、P波の直達波および地盤振動は \(1/l^{2}\)におおよそ比例していることが分かる。
水平載荷では、地盤振動が鉛直載荷ほど顕著に現れておらず、直達波と反射波によって応答は特徴付けられている。特に載荷方向に対して直角方向に観測点を採った \(U_{θx}\) ではRayleigh波およびP波の影響がほとんど現れておらず、SH波の直達波と反射波が卓越しており、その振幅も大きい。また、これらの幾何減衰の傾向については、鉛直方向載荷と同様の傾向が見られる。
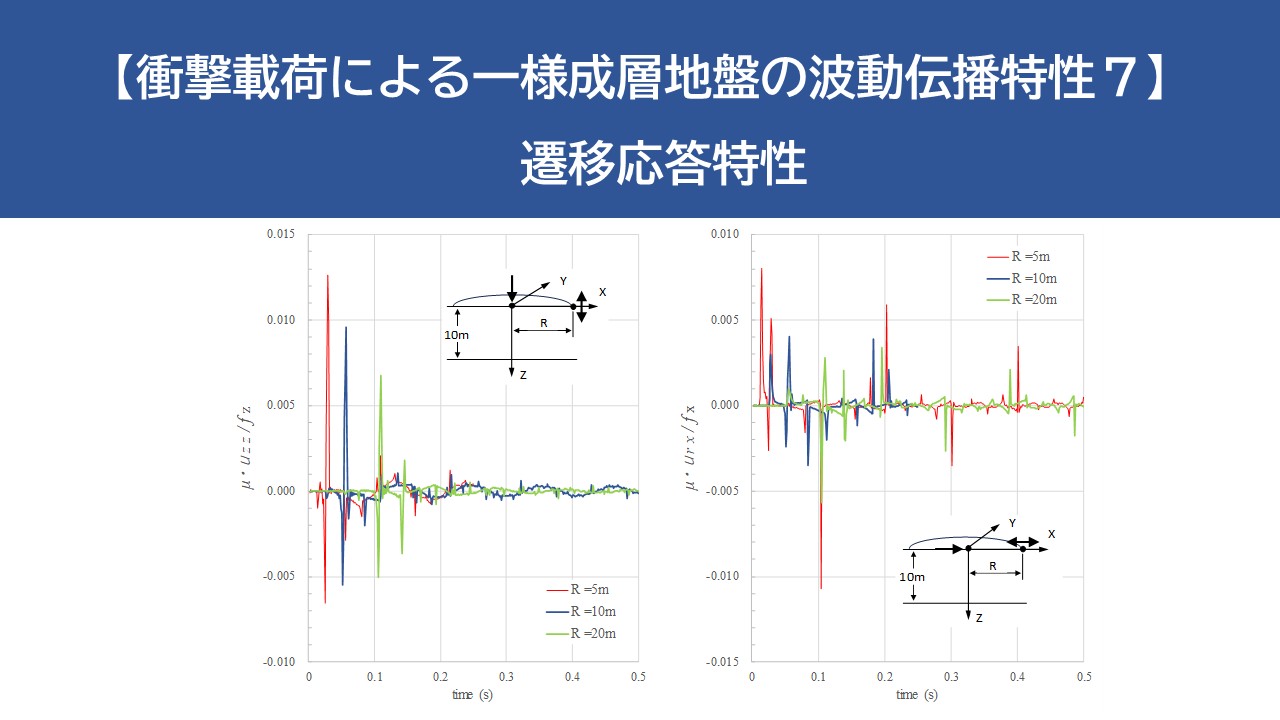
距離減衰の傾向
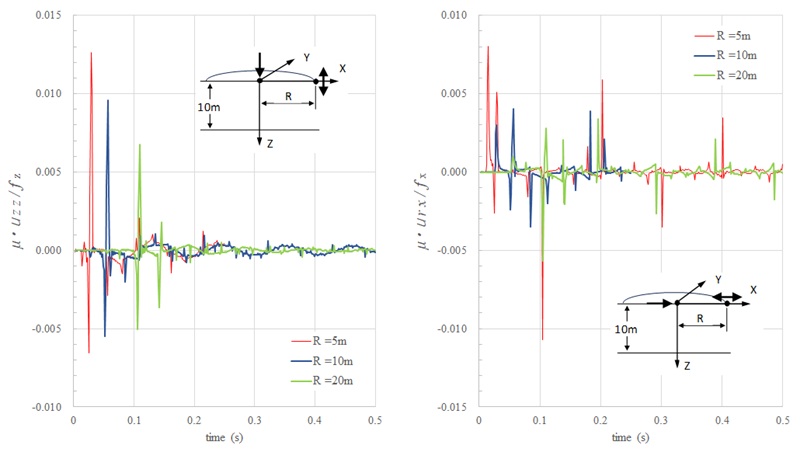
つぎに、各波動成分の距離減衰を調べるために、層厚を10mに固定し、観測点までの距離のみを変化させた変位応答を示す。ただし、無次元化表示は行っていない。同図からは、観測点までの距離によって位相の異なる反射波や地盤振動が現れていることが現れていることが分かる。しかし、Rayleigh波についてはほぼ \(1/\sqrt{R}\)に比例した振幅を示しており、層厚に影響を受けない地盤表面上を伝播する波であることが分かる。地盤振動の振幅については、5m地点と10m地点ではあまり差が見られないのに対して、20m地点ではおおよそ \(1/\sqrt{R}\)~ \(1/R^{5/6}\)倍になっており、載荷点近傍(1D程度)と遠方では距離減衰が変わるものと考えられる。また、3次元弾性体でのAiry相の距離減衰は \(1/R^{5/6}\)程度であると言われており、地盤振動がAiry相の影響によるものと思われる。さらに、前述した相似比との関係から、層厚に対する地盤振動の振幅は、おおよそ \(1/D^{2}\)~ \(1/D^{3/2}\)に比例するものと考えられる。実体波の距離減衰については位相および地表面上での入射角が異なるため、同図からの確認は難しいが、波動伝播経路距離に反比例した距離減衰を示すものと考えられる。
\(ν=0.45\) の場合の地表面変位応答
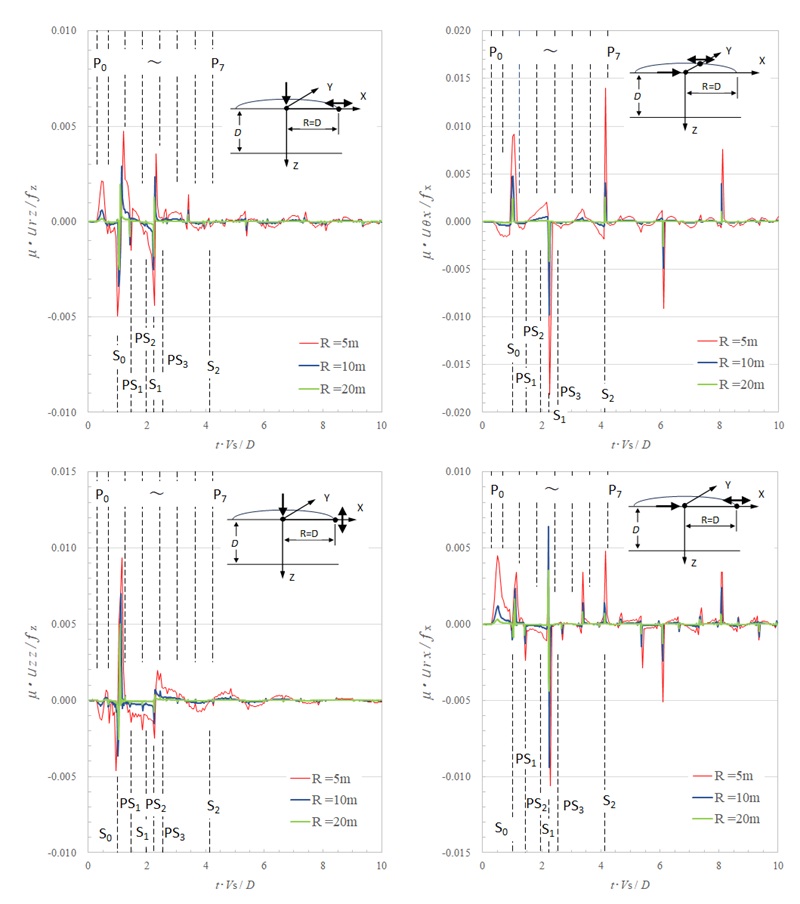
下図は、\(V_{s}=200m/s\) , \(V_{p}=663.32m/s\) , \(ν=0.45\) の地盤に、ディスク半径 \(r_{d}=0.5m\) 、 \(Δt=0.00125s\) の地表面衝撃載荷による地表面での時刻歴変位応答を示す。\(ν=0.3\) の応答と比べると、それぞれの変位は同じ波動成分から成っており、それら振幅の幾何減衰については同じ傾向にある。しかし、それぞれの変位成分において、P波が関係する直達波および反射波で変化が見られ、P波成分およびRayleigh波成分の振幅が落ちているのが分かる。ポアソン比0.3の場合には時刻 \(S_{1}\)ではS波成分の振幅が大きく現れているが、これは \(P_{2}\)と複合した波形であったためであると考えられる。このことは、SH波が卓越する \(U_{θx}\) ではポアソン比による変化がほとんど見られないことからも分かる。
ただし、ポアソン比0.3の場合に特徴的であった鉛直載荷時の地盤振動は、ポアソン比を0.45とすることで減衰が強く現れているものの、その振動数はほぼ同じであり、振動学での鉛直方向の固有振動数 \(V_{p}/4D\) とは異なる。
以上より、成層地盤での遷移応答は、その層構成および物性値よりなる分散特性によって特徴づけられ、同問題を議論する場合には、このことをよく理解したうえで検討しなくてはならない。
地中衝撃載荷による地表面変位応答
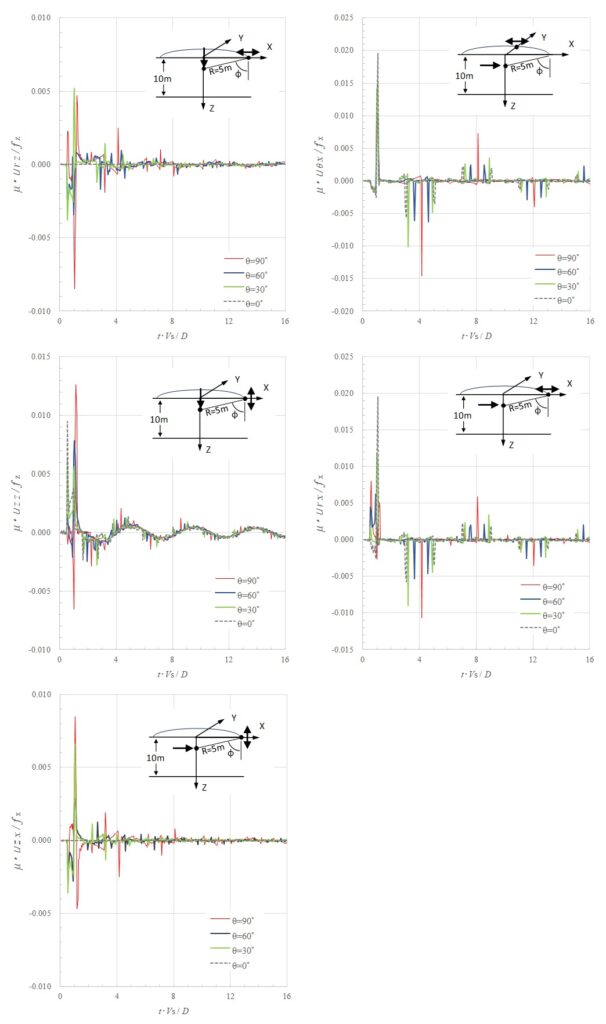
下図は地中衝撃載荷による地表面上の変位の時刻歴であり、解析モデルは層厚10m、観測点から角度 \(φ\)、距離5mの地中にディスク半径 \(r_{d}=0.5m\) 、 \(Δt=0.00125s\) の地表面衝撃載荷を行う。地盤パラメータは、\(V_{s}=200m/s\) , \(V_{p}=374.17m/s\) , \(ν=0.3\) とした。
鉛直載荷では、地中衝撃載荷においても地表載荷と同様に、直達波到達後に地盤振動が現れており、その振幅および周期は載荷位置によって変わらない。また、SH波が卓越する \(U_{θx}\) では到達後の波形が載荷位置によって変わらないが、他の変位成分では載荷位置による差が現れている。地表面近傍での載荷に対してはRayleigh波が卓越し、深くなるにつれて鉛直載荷ではP波が、水平載荷ではS波が卓越している。反射波は地表面載荷での到達時刻の前後に載荷深さに応じた時刻に現れており、その振幅は水平載荷に対するものが鉛直載荷に比べて大きい。
最後に
これまで、剛基盤を有する一様成層地盤の衝撃載荷による遷移応答解を、時間に関してラプラス変換、波数積分に離散化波数法を適用することによって誘導しました。その結果、時間・空間領域解は各波数に対する固有モードの重ね合わせとして表現されました。そして、波動の分散特性および数値計算時のパラメータによる解の精度についての検討、遷移応答特性に関する検討を行いました。その結果、一様成層地盤での分散特性および遷移応答特性を明らかにすることができたのではないかと思います。
次回より、今回の知見を移動荷重に関する数値計算に応用していきます。


コメント