修正震度法を取り入れ始めた時代に、Housnerらの研究(G.W.Housner:Behavior of Structures During Earthquakes,Journal of E.M.Division Proceedings ASCE,pp.109-129,Oct.1959)で絶対加速度応答スペクトル、速度応答スペクトル、変位応答スペクトルの間に近似が可能な関係があることが報告されています。これらの関係から近似的に作成した応答スペクトルを疑似応答スペクトルと呼んでいるようです。
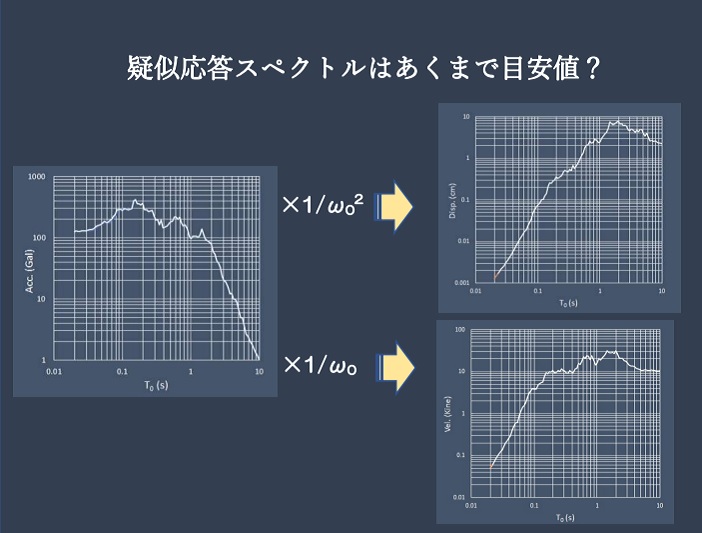
計算機の能力が上がった今の時代には、簡単に地震波から直接各応答スペクトルを出すのに手間は掛かりません。しかし、設計の途中で、加速度応答スペクトルがあるけれど変位応答スペクトルが計算されておらず、構造物の変位を大まかに知りたいといった場合には、構造物の固有角振動数の2乗で加速度応答スペクトルを割った値を参考にする場合もあります。
ここでは、疑似応答スペクトルと応答スペクトルを比較して、その精度を検証してみたいと思います。
疑似応答スペクトルの定義
各応答スペクトルの間には以下のような近似関係があります。
$$u_{max}=\frac{T_0}{2π}S_V=\frac{1}{ω_0}S_V=S_D\tag{1}$$
$$\dot{u}_{max}=S_V\tag{2}$$
$$(\ddot{u}+\ddot{u}_G)_{max}=\frac{2π}{T_0}S_V=ω_0・S_V=S_A\tag{3}$$
ここで、\(T_0\) は非減衰固有周期(\(=2π/ω_0\) ),\(S_A\) は加速度応答スペクトル,\(S_V\) は速度応答スペクトル,\(S_D\) は変位応答スペクトルです。
たしかに、単振動の変位を \(U(ω)e^{iωt}\) と表せば、速度は時間 \(t\) で微分して \(iωU(ω)e^{iωt}\)、加速度はさらに時間 \(t\) で微分して \(-ω^2U(ω)e^{iωt}\) ですので、上式の関係は容易に想像が付きます。
疑似応答スペクトルの試算例
疑似応答スペクトルを下図の地震波に対して、減衰定数 \(h=0.05\) の場合と、\(h=0.20\) の場合について算定してみます。
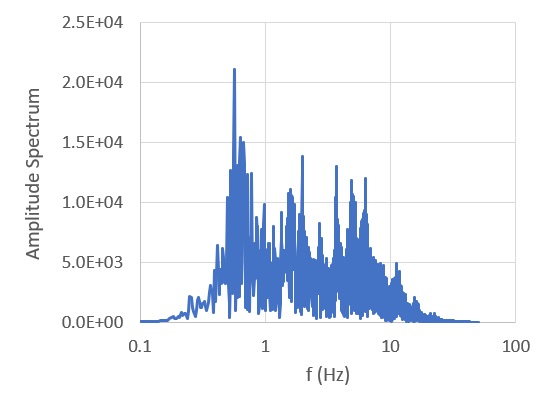
減衰定数 \(h=0.05\) の場合と、\(h=0.20\) の場合の伝達関数を図示したものを示しますが、減衰定数が大きくなるとピーク値が落ちていきます。また、固有振動数が小さくなる(長周期になる)と伝達関数はのピークは大きくなり、かつ静的に近づくと一定値に収束します。固有振動数が大きくなる(短周期になる)と伝達関数は小さくなり、ほぼ対数上で直線上に重なります。
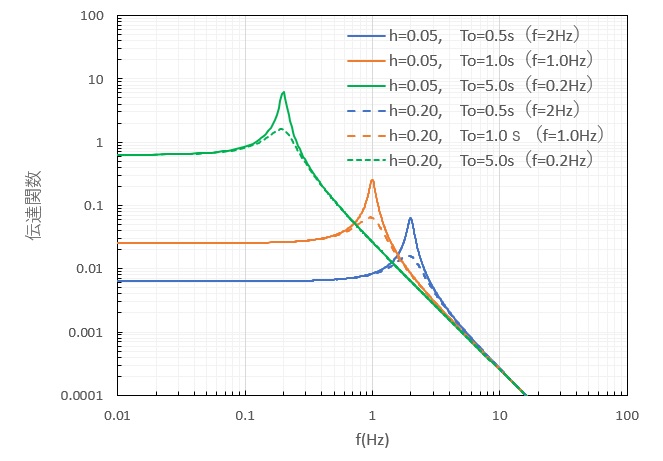
ここでは、算定された加速度応答スペクトルから、疑似速度スペクトルと疑似変位スペクトルを算定しました。
疑似応答スペクトルの精度と注意点
固有周期が0.2~0.3sより小さい範囲や、2s程度より大きい範囲では、誤差が大きくなる傾向にあります。また、減衰が小さくなると疑似相当スペクトルの精度が向上するとも言われていますが、速度については減衰が小さくても誤差は大きい傾向にあります。
したがって、一般的な地震波の卓越周期を考慮すると、加速度応答スペクトルから算定する疑似応答変位は設計時に参考にしても問題無さそうです。しかし、速度については誤差が大きく問題があると言えそうです。
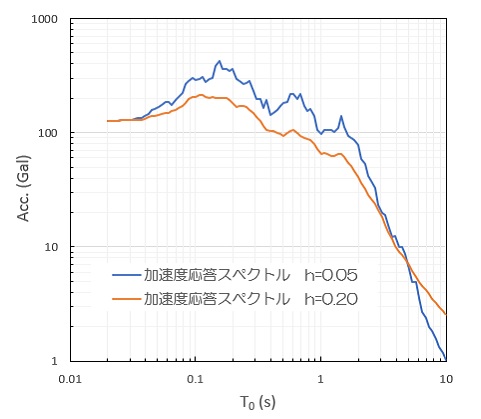
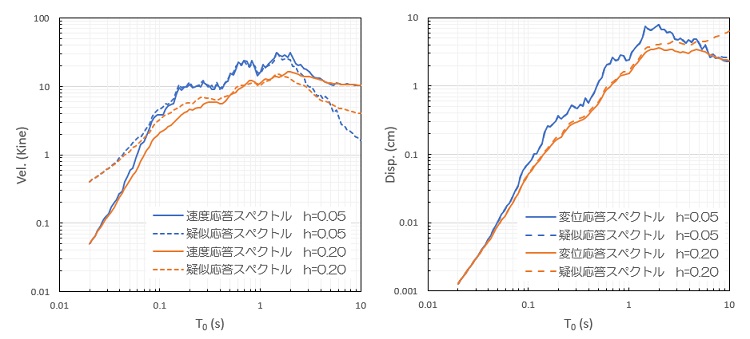
以上、参考になれば幸いです。
なお、今回の比較検討においては、「小堀ら:疑似地震動に関する応答スペクトル,土木学会論文報告集第198号,Feb.1972」に示される疑似応答スペクトルに対する考察を参考にさせていただきました。






コメント